
目录 第一章 勾股定理 1探索勾股定理……1 第1课时探索勾股定理…1 第2课时 勾股定理的验证… 2一定是直角三角形吗……… 3勾股定理的应用…8 第二章实数 1认识无理数 小… 11 2平方根 小 第1课时算术平方根… 13 第2课时平方根… 15 3立方根… 17 4估算… 19 5用计算器开方 21 6实数… 23 第1课时实数的分类、性质与运算 23 第2课时 实效与数轴…… 0… 26 7二次根式 28 第1课时 二次根式及其性质… 28 第2课时 二次根式的乘除与加减… 30 第3课时 二次根式的混合运算… 33 第三章位置与坐标 1确定位置 35 2平面直角坐标系… 38 第1课时平面直角坐标系的认识…………… 38 第2课时特殊点的坐标特征… 40 3轴对称与坐标变化… 43 第四章 一次函数 1函数… 46 2一次函数与正比例函数… 48 3一次函数的图象… 51 第1课时正比例函数的图象及性质… 51 第2课时一次函数的图象及性质… 53 4一次函数的应用… 55 第1课时确定一次函数的表达式… 55 第2课时一次函数的应用(1) 58 第3课时一次函数的应用(2)… 60 1

目录 第五章 二元一次方程组 1 认识二元一次方程组… 63 2 求解二元一次方程组… 65 第1课时 代入法解二元一次方程组… 65 第2课时 加减法解二元一次方程组… … 67 3应用二元一次方程组—鸡兔同笼 4 应用二元一次方程组—增收节支 …小………… 73 5 应用二元一次方程组一里程碑上的数 75 6 二元一次方程与一次函数… 78 7用二元一次方程组确定一次函数表达式 80 8 三元一次方程组… 83 第六章 数据的分析 1平均数 85 第1课时平均数(1) 85 第2课时平均数(2) 2中位数与众数… Sy 3从统计图分析数据的集中趋势 91 4数据的离散程度… 94 第1课时极差与方差 94 第2课时 数据分析的综合运用… 96 第七章平行线的证明 1为什么要证明 …… 99 2定义与命题… 101 第1课时定义与命题… 101 第2课时公理与定理 103 3平行线的判定… 105 4平行线的性质… 107 5三角形内角和定理: 110 第1课时三角形内角和定理的证明 110 第2课时 三角形的外角 112 检 测 第一章检测 …115 第五章检测 …131 第二章检测 …4… 118 第六章检测 …4…… 134 第三章检测 121 第七章检测 。。。+。”。n车 138 第四章检测 125 期末检测 141 期中检测 …128 2

第一章 勾股定理 1 探索勾股定理 第1课时 探索勾股定理 基础·自主梳理 1.直角三角形两直角边的平方和等于斜 (2)a,b,c之间有什么关系?(用关系式 边的平方 表示) 如果用a,b和c分别表示直角三角形的 答案a+b=c2 两直角边和斜边,那么a+b=c。 温馨提示 2.勾股定理的变形:若用a,b和c分别表 1.勾股定理的前提是直角三角形,非 示直角三角形的两直角边和斜边,则a2=c2- 直角三角形的三边之间不存在这种关系. 9=2-¥ 2.在应用勾股定理时,必须分清哪条 口(小正方形的边长为1) 边是直角边,哪条边是斜边.尤其在记忆 a2+b2=c2时,注意此关系式只有当c是斜 边时才成立.若b是斜边,则关系式是a十 2=;若a是斜边,则关系式是+2=a2. (1)a2=16,b2=9,c2=25; 核心·重难探究 知识点一勾股定理 【例1】在直线1上依次摆着几个正方形 (如图),已知斜放的三个正方形的面积分别 S S 为1,2,3,正放的四个正方形的面积分别是 S1,S2,Sa,S,则S十S2十S十S等于(B). A.3 B.4 C.5 D.6 1

儿家庭作业·数学·八年级·上册·配北师大版 思路分析正放的四个正方形的边长与斜 解在Rt△ABC中, 放的三个正方形的边长有什么关系?面积呢? 由匀股定理,得AC+BC=AB, 所以BC2=AB2-AC2=132-52=122 【规律总结】 因为BC>0,所以BC=12cm. 勾股定理是利用面积关系得到的,反过 设AD=Xcm,则BD=AB-AD=(13-咖m. 在Rt△ACD中,CD=AC-AD=5子-X; 来也可以利用勾股定理解决与面积有关的问 在Rt△BCD中,CD2=BC2-BD2= 题.解此题的关键是将四个正放的正方形的 122-(13-x2, 面积转化为斜放的正方形的面积 所以52-X=122-(13-x9, 知识点二利用勾股定理求儿何图形中 解得 总即AD-=急m 线段的长度 【例2】如图所示,在 所以CD=AC-AD=子- △ABC中,∠ACB=90, 所以CD= 6 3cm. CD是高.若AB=13cm, AC=5cm,求CD的长. 【解题总结】 思路分析在△ABC中,先由勾股定理求 在有公共直角边的两个直角三角形中分 BC的长,再分别在Rt△ACD,Rt△BCD中,由 别用勾股定理,根据公共直角边相等可以构 勾股定理建立等量关系求AD的长(或BD的 造方程,通过解方程求得结果.这种方程思想 长).进而利用勾股定理即可求出CD的长 在直角三角形的有关计算中经常用到. 新知·训练巩固 1.在直角三角形中,若勾为3,股为4,则弦 4.在△ABC中,AB=AC=13cm,BC=10cm 为(A). (1)求高AD的长; A.5 B.6 C.7 D.8 (2)求△ABC的面积. 2.已知三个正方形的面积如图,则正方形A 解(1)在△ABC中,因为AB=AC,AD为边 的边长为(B). BC的高, A.36 100 64 所以B0=2BC=2x10=5cm B.6 C.8 在Rt△ABD中,由勾股定理,得AD= D.10 AB-BD=13-5子=12.所以AD=12cm. 3.若直角三角形的两条直角边长分别为6和 (2)SM0BC AD-1012- 8,则它斜边上的高为号: 24 60(cm2). 2

第一章勾股定理 素能·演练提升 1.若一个直角三角形的三边长分别为3,4,x, 4.求下列各图中阴影部分的面积: 则x2为(D). (1 12 cm (2) A.5 B.25 C.7 D.7或25 13 cm 7 cm 2.在△ABC中,∠C=90°,周长为60,斜边与 25 cm 一条直角边的比为13:5,则这个三角形的 解(1)设正方形的边长为×cm,由题图, 三边长分别为(D). 得X=13-12=25,则阴影部分的面积为 A.5,4,3 B.13,12,5 25cm2, C.10,8,6 D.26,24,10 (2)设半圆直径为dcm,由勾股定理, 3.对角线互相垂直的四边 得dP=252-7=576,则d=24,S*m= 形叫做“垂美”四边形, 3(g}=2m×12=72m6m,即用岁 现有如图所示的“垂美” 部分的面积为72πcm. 四边形ABCD,对角线 C D AC,BD交于点O.若AD=2,BC=4,则 AB2+CD2=20. 第2课时 勾股定理的验证 基础·自主梳理 验证勾股定理 (1)大正方形的边长可以表示为a+b, 操作:剪四个与图1完全相同的直角三 面积可以表示为(a+b, 角形,然后将它们拼成如图2所示的图形: (2)大正方形由4个三角形和1个小正 方形组成,面积可以表示为4x2ab+c, 归纳:对比两种表示方法,可以得到等 式:(a+b9=4x2ab+c. 整理,得a+b=c2 图1 图2 3

儿家庭作业·数学·八年级·上册·配北师大版 温馨提示 理的正确性.在一些几何问题中,对图形 利用拼图来验证勾股定理,就是根据 进行割补拼接后,只要没有重叠,没有空 同一个图形(或两个全等的图形)面积的 隙,面积就不会改变 不同表示方法列出等式,从而验证勾股定 核心·重难探究 知识点一勾股定理的验证 知识点二 勾股定理的简单应用 【例1】用如图1所示的四个相同的直角 【例2】有一架飞机在空中水平飞行,某一 三角形(直角边为a,b,斜边为c),可以拼成如 时刻刚好飞到一个男孩头顶正上方4000m处, 图2所示的正方形.你能用图2验证勾股定 过了20s,飞机距离这个男孩头顶5000m, 理吗?说明理由. 则飞机每时飞行多少千米? 思路分析(1)根据题意画出图形,这个 图形是直角三角形吗?(2)在画出的三角形 中,已知什么?求什么?你会用勾股定理求 解吗?(3)欲求飞机每时飞行多少千米,就应 图1 图2 该知道其20s时间里飞行的路程是多少. 思路分析你能用两种方法表示图2中 解如图,在△ABC中,∠C=90°,AC= 大正方形的面积吗?这两种表示方法有什么 4000m=4km,AB=5000m=5km 关系? 由勾股定理,得BC2=AB- 解能验证勾股定理理由如下: AC=52-42=9=3,所以BC= 3 km. 大正方形的边长为C其面积可以表示为C 即飞机20s飞行3km,所以它每时飞行 大正方形的面积也可以看作是小正方形的 面积加上4个直角三角形的面积,即(b-a+ 的距离为3600x3=540km. 20 4×2ab, 【方法归纳】 所以C=b-a+4x2ab,卷理,得+ 根据题意画出正确的图形是解决问题的 b2=c2. 关键.问题的解决既体现了数学模型意识,又 体现了数形结合思想.同时要注意单位的 【方法归纳】 换算. 用不同的代数式表示同一个图形的面 积,由此建立相等关系,化简得出结论 4

第一章勾股定理 新知·训练巩固 1.张大爷离家出门散步,他先向正东走了 三角形拼成如图所示的图形.在Rt△ABC 30m,接着又向正南走了40m,此时他离 中,∠ACB=90°,若AC=b,BC=a,请你利 家的距离为(C). 用这个图形解决下列问题: A.30m B.40m C.50m D.70m (1)试说明a2+2=c2; 2.如图,在高为5m,坡面长为13m的楼梯表 (2)如果大正方形的面积是10,小正方形的 面铺地毯,地毯的长度至少需要17m. 面积是2,求(a十b)2的值. 解(1)因为大正方形面积为C,直角三角形 13m 面积为2ab,小正方形面和为(b-a,所以 3.中国古代数学家们对 d=4x ab+(a-bF=2ab+a-2ab+ 于勾股定理的发现和 b,即c2=a2+b2. 证明,在世界数学史 上具有独特的贡献和 2由题图可知,b-aY=2,4×2ab= 地位,体现了数学研 10-2=8,所以2ab=8, 究中的继承和发展.现用4个全等的直角 所aa+by=(b-a旷+4ab=2+2×8=18. 素能·演练提升 1.下列选项中,不能用来证明勾股定理的 3.如图,盒内长、宽、高分别是6cm,3cm, 是(D). 2cm,盒内可放木棒最长的长度是(B). e c D 2.如图所示,台风过后某小 A.6 cm B.7 cm C.8 cm D.9 cm 学的旗杆在B处断裂,旗 4.如图,某小区有一块直角三角形的绿地,量 杆顶部A落在离旗杆底 得两直角边AC=4m,BC=3m,考虑到这 部点C8m处,已知旗杆长16m,则旗杆断 块绿地周围还有足够多的空余部分,于是 裂的地方距底部(C). 打算将这块绿地扩充成等腰三角形,且扩 A.4m B.5 m C.6m D.8 m 充部分是以AC为一直角边的直角三角形, 5
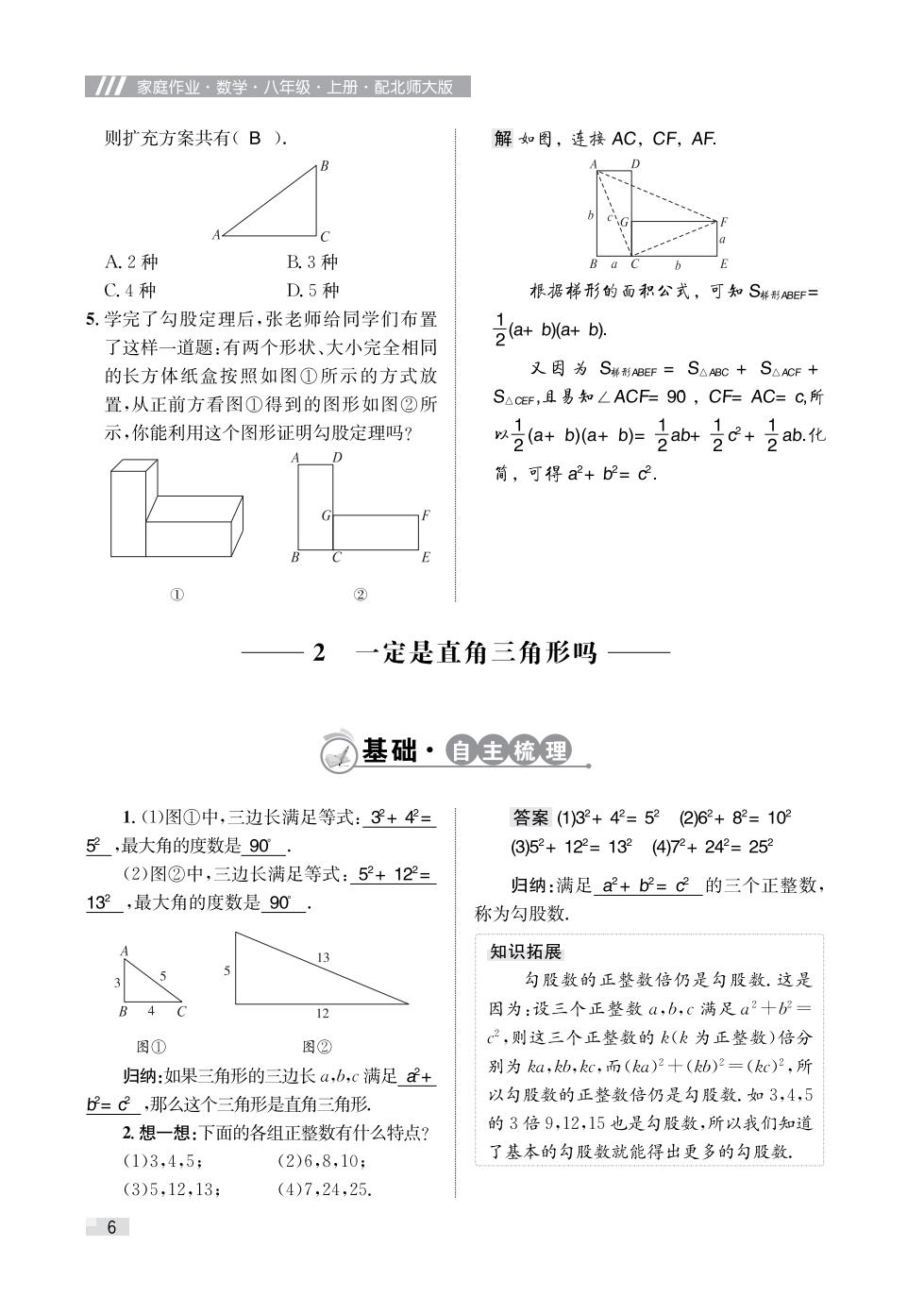
家庭作业·数学·八年级·上册·配北师大版 则扩充方案共有(B). 解如图,连接AC,CF,AF A.2种 B.3种 B a C 6 C.4种 D.5种 根据梯形的面积公式,可知S样形8EF= 5.学完了勾股定理后,张老师给同学们布置 了这样一道题:有两个形状、大小完全相同 2a+b以a+b以 的长方体纸盒按照如图①所示的方式放 又因为S梯形BEF=SAABC+S△ACF+ 置,从正前方看图①得到的图形如图②所 SACEF,且易知∠ACF=90,CF=AC=C,所 示,你能利用这个图形证明勾股定理吗? 以2a+ba+b)=2ab+2c+2ab.化 A 简,可得a+b=c2. ② 2一定是直角三角形吗 基础·自主梳理 1.(1)图①中,三边长满足等式:3+4= 答案(1)32+42=52(2)6+82=10 子,最大角的度数是90 3)52+122=132(4)72+242=252 (2)图②中,三边长满足等式:5+12= 归纳:满足a+b2=c的三个正整数, 13,最大角的度数是90 称为勾股数 3 知识拓展 勾股数的正整数倍仍是勾股数.这是 12 因为:设三个正整数a,b,c满足a2十b 图① 图② c2,则这三个正整数的k(k为正整数)倍分 归纳:如果三角形的三边长a,b,c满足子+ 别为ka,kb,kc,而(ka)2十(kb)2=(kc)2,所 仔=C,那么这个三角形是直角三角形 以勾股数的正整数倍仍是勾股数.如3,4,5 2.想一想:下面的各组正整数有什么特点? 的3倍9,12,15也是勾股数,所以我们知道 (1)3,4,5; (2)6,8,10: 了基本的勾股数就能得出更多的勾股数 (3)5,12,13; (4)7,24,25. 6

第一章勾股定理 核心·重难探究 知识点一直角三角形的判别条件 定最长边,算出最长边的平方及另两边的平 【例1】如图所 B 方和,如果最长边的平方与另两边的平方和 示,在四边形ABCD 相等,那么此三角形为直角三角形 中,AD=3cm,AB= 知识点二勾股数 4cm,∠BAD=90°, 【例2】判定下列各组数是不是勾股数: BC=12cm,CD=13cm.求四边形ABCD的 (1)7,24,25;(2)8,15,19;(3)0.6,0.8, 面积. 1.0;(4)3n,4n,5n(n>1,且n为自然数). 思路分析怎样将四边形转化为两个三 思路分析(1)各组数中的三个数都是正 角形?这两个三角形都是直角三角形吗?你 整数吗?(2)是正整数的三个数满足a2十 是怎样得到的?你能分别求出这两个三角形 b=c2吗? 的面积吗? 解(1)因为7,24,25都是正整数,且7+ 解如图所示,连 242=252,所以7,24,25是勾股数. 接BD. (2)因为82+15≠192,所以8,15,19不是 在△ABD中,AD= 勾股数. 3cmAB=4cm,∠BAD= (3)因为0.6,0.8,1.0不是正整数, 90. 所以0.6,0.8,1.0不是勾股数. 根据勾股定理,得BD=AD+AB=3+ (4)因为n>1,且n为自然数, 42=5,所以BD=5cm. 所以3n,4n,5n都是正整数. 在△BCD中,BD=5cm,BC=12cm,CD= 又(3nY+(4n2=25㎡=(5n}, 13cm,且5+12=13,所以BD+BC=CD, 所以3n,4n,5n(n>1,且n为自然数)是勾 所以△BCD是直角三角形.所以S知边形eCD= 股数 0+5 12-3 【误区警示】 【规律总结】 一组数是勾股数必须满足两个条件:(1)都 利用三角形的三边长之间的关系判断一 是正整数:(2)满足a2+=2.两者缺一不可. 个三角形是不是直角三角形的思路是:先确 新知·训练巩固 1.下列各组数是勾股数的是(D). 3.分别以下列各组数为一个三角形的三边长: A.7,12,13 B.3,4,7 ①6,8,10;②13,5,12;③2,2,3:④7,24,25 C.0.6,0.8,1 D.60,80,100 其中能构成直角三角形的有(B)组, 2.下列四组线段中,可以构成直角三角形的 A.2 B.3 C.4D.5 一组是(D). 4.在△ABC中,a=3,b=7,c2=58,则S△ABc A.1,2,3 B.32,42,5 21 c片 2 D.0.3,0.4,0.5 7

儿家庭作业·数学·八年级·上册·配北师大版 素能·演练提升 1.已知△ABC的三边分别为a,b,c,则下列 4.如图,网格中有一△ABC, 条件不能判定△ABC是直角三角形的 若小方格的边长为1,请 是(A). 你根据所学的知识, A.∠A:∠B:∠C=3:4:5 (1)求△ABC的面积: B.a:b:c=5:12:13 (2)判断△ABC是什么形状,并说明理由. C.∠C=∠A-∠B 解(1)△ABC的面和=4×4-1×2÷2-4× D.b2=a2-c2 3÷2-2×4÷2=16-1-6-4=5.故△ABC 2.若一个直角三角形的面积为6cm,斜边长 的面积为5. 为5cm,则该直角三角形的周长为12cm ②)因为小方格的边长为1,所以AB=1P+ 3.已知a,b,c是△ABC的三边长,若|a-bl+ 2=5,AC=2+4=20,BC=32+4=25, |a2+2一c2|=0,则△ABC是等腰直角 所以AB+AC=BC,所以△ABC为直 三角形 角三角形. 3勾股定理的应用 基础·自主梳理 1.解决几何体表面上两点之间的最短距 的两点之间的距离,则直接利用“两点之间线 离问题的关键是要设法把立体图形转化为平 段最短”求出线段的长度即可;若计算不同面 面图形,具体步骤是: 上的两点之间的距离,则必须把长方体(或正 (1)把立体图形展成平面图形; 方体)的表面展开,使两点转化到同一个平 (2)确定点的位置; 面内,就可以利用“两点之间线段最短”和 (3)确定直角三角形; 勾股定理加以解决了, (4)分析直角三角形的边长,用勾股定 3.用勾股定理解决实际问题的关键是从 理求解. 实际问题中构建数学模型一直角三角 2.长方体(或正方体)是立体图形,但它 形,再正确利用“两点之间线段最短”以及 的每个面都是平面,所以若计算同一个面上 勾股定理解答. 8