
家庭值四 第2课时 平行四边形的对角线的性质
第2课时 平行四边形的对角线的性质

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.平行四边形的对角线的性质 定理 平行四边形的对角线互相平分 温馨提示 1.平行四边形的性质可以从边、角、对角线三个方面掌握 2.平行四边形的一条对角线分成的两个三角形全等;平行四 边形被两条对角线分成的四个小三角形的面积相等,相邻两 个三角形周长之差等于平行四边形两邻边长度之差. 导航页
导航页 基础自主梳理 1.平行四边形的对角线的性质 定理 平行四边形的对角线互相__________. 温馨提示 1.平行四边形的性质可以从边、角、对角线三个方面掌握. 2.平行四边形的一条对角线分成的两个三角形全等;平行四 边形被两条对角线分成的四个小三角形的面积相等,相邻两 个三角形周长之差等于平行四边形两邻边长度之差. 平分

2.已知口ABCD,下列结论不一定成立的是(D) A.∠A+∠B=180° B.AD-BC C.对角线AC与BD互相平分 D.∠B=∠C 导航页
导航页 2.已知▱ABCD,下列结论不一定成立的是( ). A.∠A+∠B=180° B.AD=BC C.对角线AC与BD互相平分 D.∠B=∠C D
核心重难探究 知识点一平行四边形的对角线的性质 【例1】已知口ABCD和EBFD的顶点A,E,F,C在一条直线 上.求证:AE=CF B 思路点拨:(I)口ABCD和口EBFD的两条对角线有何特点? (2)连接BD,你能通过运用平行四边形对角线的性质证得结 论吗? 导航页
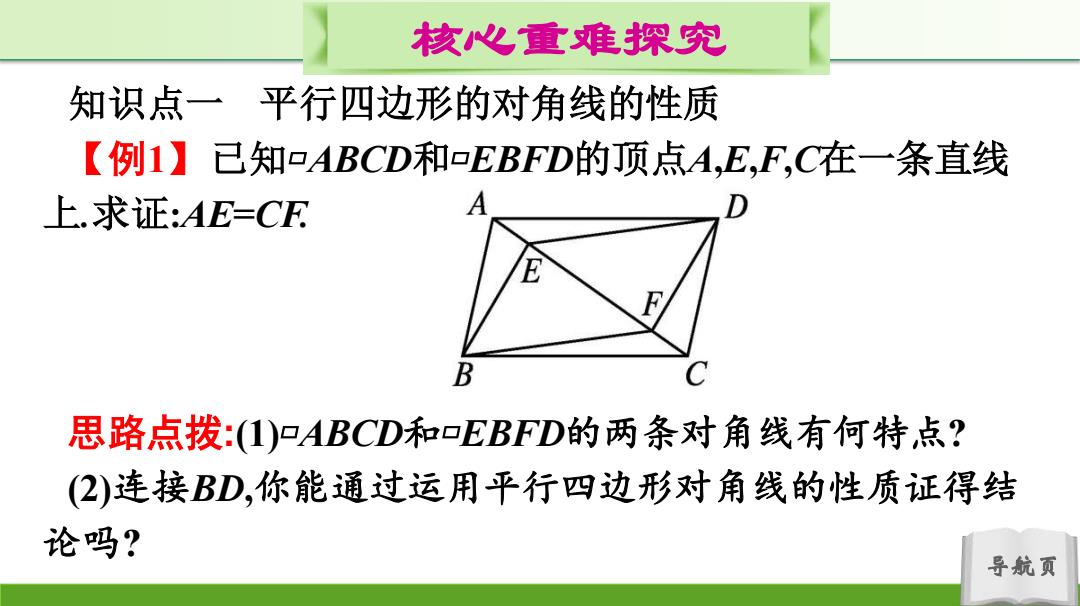
导航页 核心重难探究 知识点一 平行四边形的对角线的性质 【例1】已知▱ABCD和▱EBFD的顶点A,E,F,C在一条直线 上.求证:AE=CF. 思路点拨:(1)▱ABCD和▱EBFD的两条对角线有何特点? (2)连接BD,你能通过运用平行四边形对角线的性质证得结 论吗?
证明:连接BD,交AC于点O. A B :四边形ABCD,EBFD是平行四边形, .AO-CO.EO-FO .AO-EO=CO-FO,即AE=CF 导航页
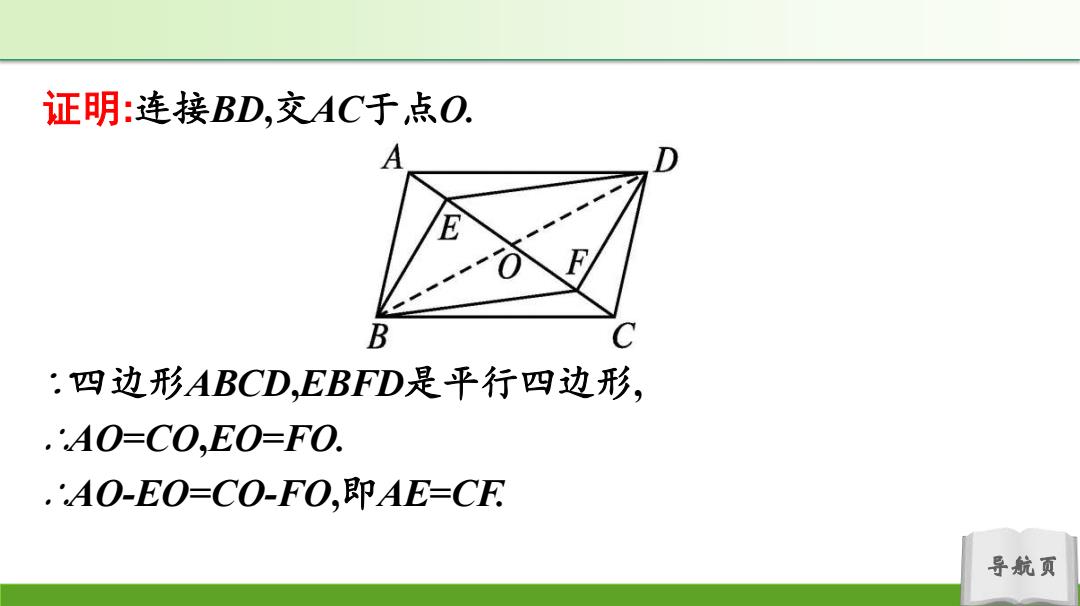
导航页 证明:连接BD,交AC于点O. ∵四边形ABCD,EBFD是平行四边形, ∴AO=CO,EO=FO. ∴AO-EO=CO-FO,即AE=CF

【方法归纳】 本题利用全等三角形知识也可以使结论获证,但相比而言, 应用平行四边形对角线的性质求证更简洁明快因此,在学习 了新知识后,要善于运用它,不受旧知识的限制与干扰,另辟蹊 径,获取最佳解题方法 导航页
导航页 【方法归纳】 本题利用全等三角形知识也可以使结论获证,但相比而言, 应用平行四边形对角线的性质求证更简洁明快.因此,在学习 了新知识后,要善于运用它,不受旧知识的限制与干扰,另辟蹊 径,获取最佳解题方法

知识点二平行四边形性质的综合运用 【例2】如图,口ABCD的对角线AC,BD相交于点O,EF经过 点O,且与AD,BC分别交于点E,F已知AB=4,BC=5,OE=1. AE (1)求四边形EFCD的周长;B (2)若AB LAC,求四边形EFCD的面积 思路点拨:(1)线段CF与AE有何数量关系?为什么? (2)四边形EFCD的面积与四边形ABCD的面积有何关系? 导航页
导航页 知识点二 平行四边形性质的综合运用 【例2】如图, ▱ABCD的对角线AC,BD相交于点O,EF经过 点O,且与AD,BC分别交于点E,F.已知AB=4,BC=5,OE=1. (1)求四边形EFCD的周长; (2)若AB⊥AC,求四边形EFCD的面积. 思路点拨:(1)线段CF与AE有何数量关系?为什么? (2)四边形EFCD的面积与四边形ABCD的面积有何关系?

解:(1):四边形ABCD是平行四边形, ..OA=OC,CD=AB-4,ADBC. .∠DAC=∠BCA. 又∠AOE=∠COF, .△AOE≌△COF .OE-OFAE-CF ..四边形EFCD的周长=EF+CF+CD+DE=2+AD+4=6+5=11. 导航页
导航页 解:(1)∵四边形ABCD是平行四边形, ∴OA=OC,CD=AB=4,AD∥BC. ∴∠DAC=∠BCA. 又∵∠AOE=∠COF, ∴△AOE≌△COF. ∴OE=OF,AE=CF. ∴四边形EFCD的周长=EF+CF+CD+DE=2+AD+4=6+5=11

(2)同理,可证△EOD≌△FOB,△COD≌△AOB. ,:四边形EFCD的面积等于平行四边形ABCD面积的一半 AB⊥AC, .AC-BC2-AB2-3. .'SABCD=ABAC=12. .,四边形EFCD的面积为6 导航页
导航页 (2)同理,可证△EOD≌△FOB,△COD≌△AOB. ∴四边形EFCD的面积等于平行四边形ABCD面积的一半. ∵AB⊥AC, ∴AC= 𝑩𝑪𝟐-𝑨𝑩𝟐 =3. ∴S▱ABCD=AB·AC=12. ∴四边形EFCD的面积为6