
家庭值亚 第3课时 平行四边形的判定与性质的应用
第3课时 平行四边形的判定与性质的应用

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.平行四边形的性质 定理平行四边形的对边 相等 定理 平行四边形的对角相等 定理平行四边形的对角线互相 平分 2.平行四边形的判定 定理两组对边分别 相等 的四边形是平行四边形 定理一组对边平行且相等的四边形是平行四边形 定理 对角线互相平分 的四边形是平行四边形 导航页
导航页 基础自主梳理 1.平行四边形的性质 定理 平行四边形的对边__________. 定理 平行四边形的对角__________. 定理 平行四边形的对角线互相__________. 2.平行四边形的判定 定理 两组对边分别__________的四边形是平行四边形. 定理 一组对边__________的四边形是平行四边形. 定理 对角线互相__________的四边形是平行四边形. 相等 相等 平分 相等 平行且相等 平分

3.两条平行线之间的距离 如果两条直线互相平行,则其中一条直线上任意一点到另 一条直线的距离都相等,这个距离称为平行线之间的距离, 温馨提示 点与点之间的距离是点到直线的距离、两条平行线之间的 距离的基础.两条平行线之间的任何两条平行线段都相等. 导航页
导航页 3.两条平行线之间的距离 如果两条直线互相平行,则其中一条直线上__________到另 一条直线的距离都相等,这个距离称为平行线之间的距离. 温馨提示 点与点之间的距离是点到直线的距离、两条平行线之间的 距离的基础.两条平行线之间的任何两条平行线段都相等. 任意一点
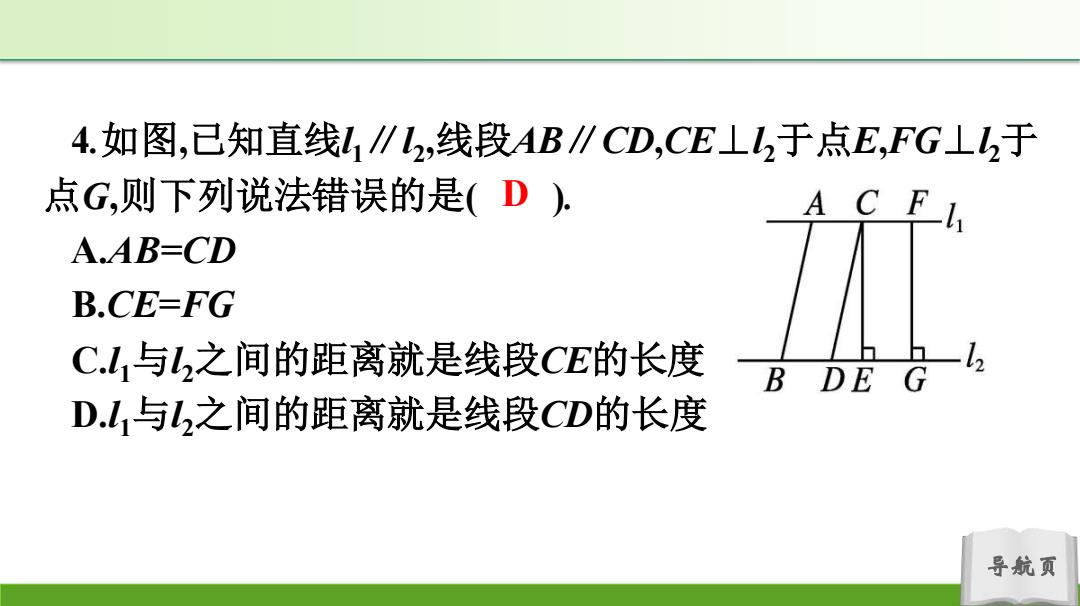
4.如图,已知直线L1∥L,线段AB∥CD,CE⊥I2于点E,FG⊥I2于 点G,则下列说法错误的是(D). A C F A.AB-CD B.CE-FG C.l1与L,之间的距离就是线段CE的长度 DE D.l1与L,之间的距离就是线段CD的长度 导航页
导航页 4.如图,已知直线l1∥l2 ,线段AB∥CD,CE⊥l2于点E,FG⊥l2于 点G,则下列说法错误的是( ). A.AB=CD B.CE=FG C.l1与l2之间的距离就是线段CE的长度 D.l1与l2之间的距离就是线段CD的长度 D
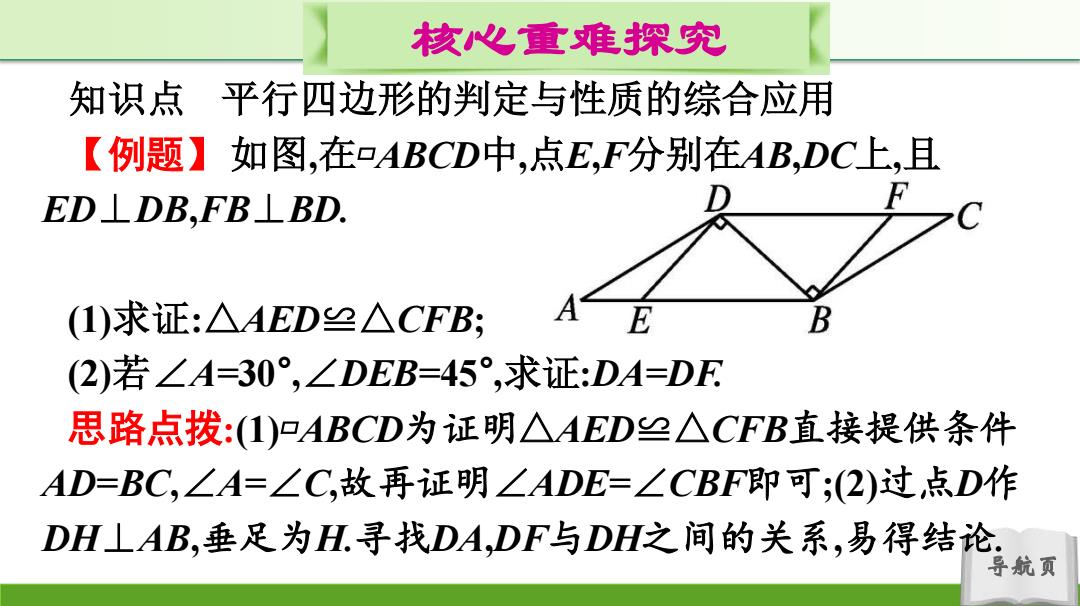
核心重难探究 知识点 平行四边形的判定与性质的综合应用 【例题】如图,在ABCD中,点E,F分别在AB,DC上,且 ED⊥DB,FB⊥BD (1)求证:△AED≌△CFB; E B (2)若∠A=30°,∠DEB=45°,求证:DA=DF 思路点拨:(I)口ABCD为证明△AED≌△CFB直接提供条件 AD=BC,∠A=∠C,故再证明∠ADE=∠CBF即可;(2)过点D作 DH⊥AB,垂足为H.寻找DA,DF与DH之间的关系,易得结论 航页
导航页 核心重难探究 知识点 平行四边形的判定与性质的综合应用 【例题】 如图,在▱ABCD中,点E,F分别在AB,DC上,且 ED⊥DB,FB⊥BD. (1)求证:△AED≌△CFB; (2)若∠A=30° ,∠DEB=45° ,求证:DA=DF. 思路点拨:(1)▱ABCD为证明△AED≌△CFB直接提供条件 AD=BC,∠A=∠C,故再证明∠ADE=∠CBF即可;(2)过点D作 DH⊥AB,垂足为H.寻找DA,DF与DH之间的关系,易得结论

证明:(1)·四边形ABCD是平行四边形, .AD=CB,∠A=∠C,AD∥BC. .·∠ADB=∠CBD. ·ED⊥DB,FB⊥BD, .:∠EDB=∠FBD=90°. .·∠ADE=∠CBF.·△AED≌△CFB. 导航页
导航页 证明:(1)∵四边形ABCD是平行四边形, ∴AD=CB,∠A=∠C,AD∥BC. ∴∠ADB=∠CBD. ∵ED⊥DB,FB⊥BD, ∴∠EDB=∠FBD=90° . ∴∠ADE=∠CBF.∴△AED≌△CFB
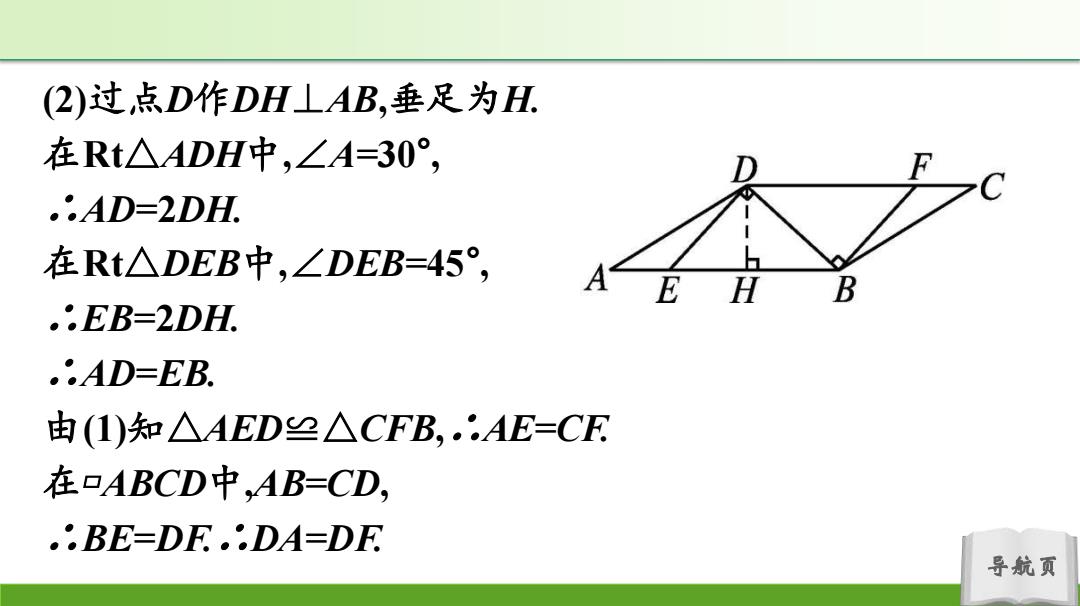
(2)过点D作DH⊥AB,垂足为H 在Rt△ADH中,∠A=30°, .AD=2DH. 在Rt△DEB中,∠DEB=45°, A ..EB=2DH. .·AD=EB. 由(1)知△AED≌△CFB,.AE=CF 在口ABCD中,AB=CD, ..BE-DE.DA-DE 导航页
导航页 (2)过点 D作DH ⊥AB ,垂足为H. 在Rt △ADH 中 , ∠A=30 ° , ∴AD= 2DH. 在Rt △DEB 中 , ∠DEB=45 ° , ∴EB= 2DH. ∴AD=EB. 由(1)知△AED ≌ △CFB , ∴AE=CF. 在 ▱ABCD 中 ,AB=CD , ∴BE=DF. ∴DA=DF

【方法归纳】 判定平行四边形的方法的选择 已知条件 证明思路 1.另一组对边相等 组对边相等 2.这组对边平行 1.另一组对边平行 组对边平行 2.这组对边相等 条对角线的中点 对角线互相平分 导航页
导航页 【方法归纳】 判定平行四边形的方法的选择 已知条件 证明思路 一组对边相等 1.另一组对边相等 2.这组对边平行 一组对边平行 1.另一组对边平行 2.这组对边相等 一条对角线的中点 对角线互相平分
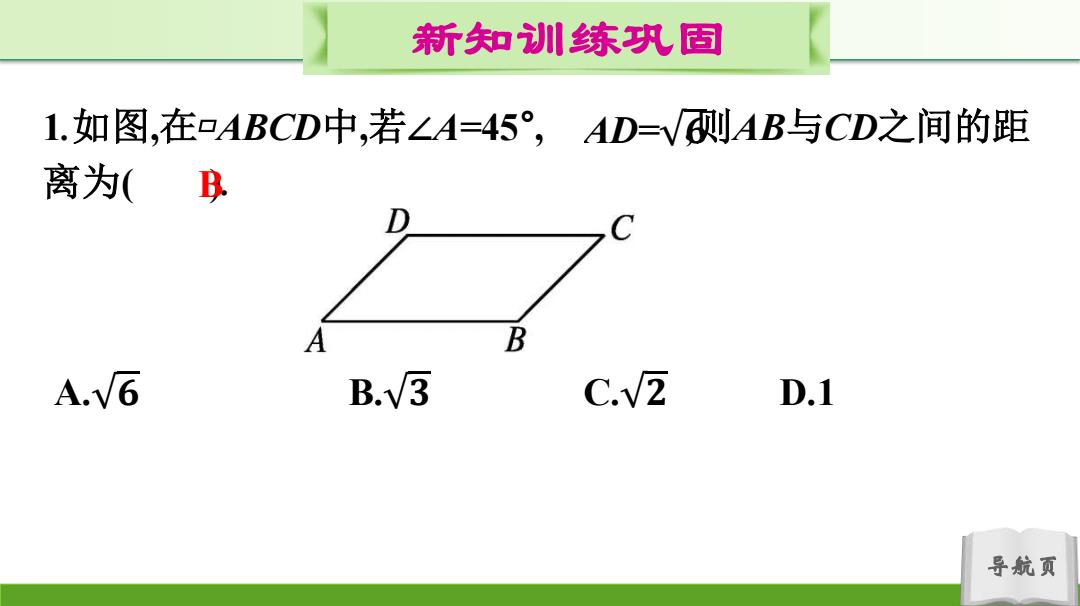
新知训练巩固 1.如图,在ABCD中,若∠A=45°,AD=V刚AB与CD之间的距 离为( B D A B A.V6 B.v3 C./2 D.1 导航页
导航页 新知训练巩固 1.如图,在▱ABCD中,若∠A=45° , ,则AB与CD之间的距 离为( ). AD= 𝟔 A. 𝟔 B. 𝟑 C. 𝟐 D.1 B