
家庭值四 第2课时 利用对角线判定平行四边形
第2课时 利用对角线判定平行四边形

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.平行四边形的判定 定理对角线互相平分 的四边形是平行四边形 2.下列条件中能使四边形是平行四边形的是(D), A.对角线互相垂直 B.对角线相等 C.对角线互相垂直且相等 D.对角线互相平分 导航页
导航页 基础自主梳理 1.平行四边形的判定 定理 对角线互相__________的四边形是平行四边形. 2.下列条件中能使四边形是平行四边形的是( ). A.对角线互相垂直 B.对角线相等 C.对角线互相垂直且相等 D.对角线互相平分 平分 D
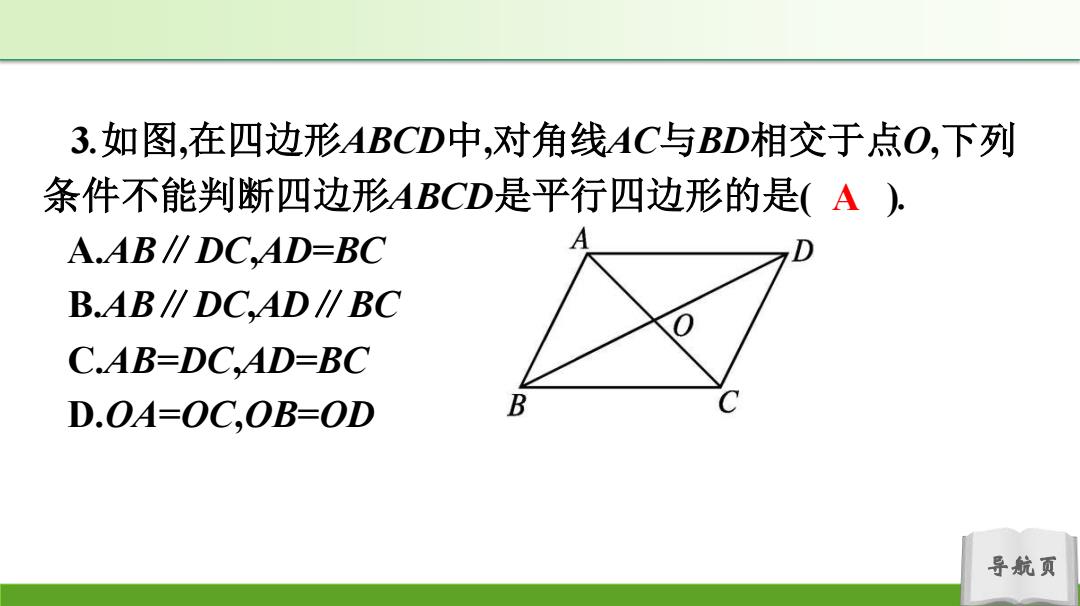
3.如图,在四边形ABCD中,对角线AC与BD相交于点O,下列 条件不能判断四边形ABCD是平行四边形的是(A). A.AB∥DC,AD=BC B.AB∥DC,AD∥BC C.AB=DC,AD-BC D.OA-OC.OB-OD B 导航页
导航页 3.如图,在四边形ABCD中,对角线AC与BD相交于点O,下列 条件不能判断四边形ABCD是平行四边形的是( ). A.AB∥DC,AD=BC B.AB∥DC,AD∥BC C.AB=DC,AD=BC D.OA=OC,OB=OD A
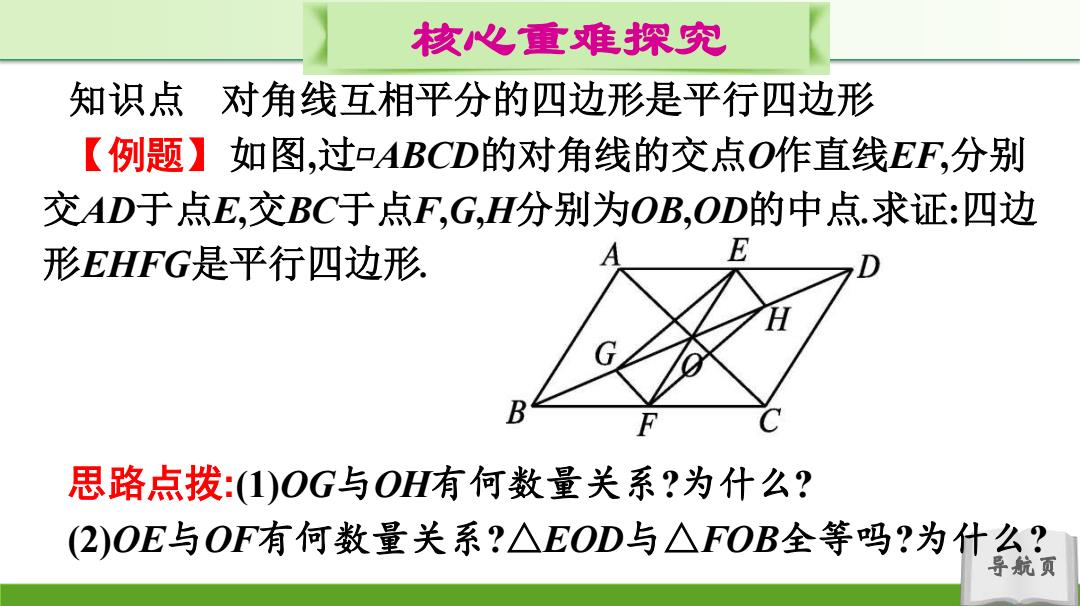
核心重难探究 知识点 对角线互相平分的四边形是平行四边形 【例题】如图,过ABCD的对角线的交点O作直线EF,分别 交AD于点E,交BC于点F,G,H分别为OB,OD的中点.求证:四边 形EHFG是平行四边形 E B 思路点拨:1)OG与OH有何数量关系?为什么? (2)OE与OF有何数量关系?△EOD与△FOB全等吗?为什么? 导航页
导航页 核心重难探究 知识点 对角线互相平分的四边形是平行四边形 【例题】如图,过▱ABCD的对角线的交点O作直线EF,分别 交AD于点E,交BC于点F,G,H分别为OB,OD的中点.求证:四边 形EHFG是平行四边形. 思路点拨:(1)OG与OH有何数量关系?为什么? (2)OE与OF有何数量关系?△EOD与△FOB全等吗?为什么?

证明:四边形ABCD为平行四边形, ..OB=OD,AD=BC,FLADII BC. .∠ADO=∠CBO. 又.∠EOD=∠FOB, .'△EOD≌△FOB(ASA) .EO=FO. 又.G,H分别为OB,OD的中点,.:GO=HO ,四边形EHFG是平行四边形. 导航页
导航页 证明:∵四边形ABCD为平行四边形, ∴OB=OD,AD=BC,且AD∥BC. ∴∠ADO=∠CBO. 又∵∠EOD=∠FOB, ∴△EOD≌△FOB(ASA). ∴EO=FO. 又∵G,H分别为OB,OD的中点,∴GO=HO. ∴四边形EHFG是平行四边形

【方法归纳】 若所证四边形中有对角线出现或原已知四边形中出现了对 角线,则用“对角线互相平分的四边形是平行四边形”这一定 理解决问题最为简便 导航页
导航页 【方法归纳】 若所证四边形中有对角线出现或原已知四边形中出现了对 角线,则用“对角线互相平分的四边形是平行四边形”这一定 理解决问题最为简便

新知训练织固 1.在四边形ABCD中,对角线AC,BD相交于点O,则下列条件:① ABII CD,ADIIBC,②AB=CD,AD=BC,③ABII CD,AB=CD;④ OA=OC,OB=OD;⑤∠BAD=∠BCD,∠ABC=∠ADC,⑥ ADIIBO,∠BAD=∠BCD.其中能使四边形ABCD是平行四边形 的有( 尖. A.6个 B.5个 C.4个 D.3个 2.在四边形ABCD中,对角线AC,BD交于点O.若OA=6,OB=8, 当0C= 6 ,0D= 8 时,四边形ABCD是平行 四边形 导航页
导航页 新知训练巩固 1.在四边形ABCD中,对角线AC,BD相交于点O,则下列条件:① AB∥CD,AD∥BC;②AB=CD,AD=BC;③AB∥CD,AB=CD;④ OA=OC,OB=OD;⑤∠BAD=∠BCD,∠ABC=∠ADC;⑥ AD∥BC,∠BAD=∠BCD.其中能使四边形ABCD是平行四边形 的有( ). A.6个 B.5个 C.4个 D.3个 2.在四边形ABCD中,对角线AC,BD交于点O.若OA=6,OB=8, 当OC=__________,OD=__________时,四边形ABCD是平行 四边形. A 6 8

3.如图,在四边形ABCD中,AC与BD相交于点O,ABII CD, OA=OC.求证:四边形ABCD是平行四边形. B 证明:ABII CD, .'∠ABO=∠CDO,∠BAO=∠DCO. 又·OA=0C,.△AOB≌△COD. .,OB=OD.四边形ABCD是平行四边形 导航页
导航页 3.如图,在四边形ABCD中,AC与BD相交于点O,AB∥CD, OA=OC.求证:四边形ABCD是平行四边形. 证明 :∵AB∥CD, ∴∠ABO=∠CDO,∠BAO=∠DCO. 又∵OA=OC,∴△AOB≌△COD. ∴OB=OD.∴四边形ABCD是平行四边形

路漫漫其修远兮 吾将上下而求索
路漫漫其修远兮 吾将上下而求索