
家庭值亚 第2课时 分式的基本性质与化简
第2课时 分式的基本性质与化简

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.分式的基本性质 分式的分子与分母都乘(或除以)同一个不等于零的整 式,分式的值不变 这一性质可以用式子表示为二 bm b b÷m a'm'a 0). a÷m 易错提示 0是分式基本性质的一个制约条件.运用分式的基本性质 时,要注意两个“同时”:一是分式的分子与分母同时作乘法或 除法运算;二是乘(或除以)的对象必须是同一个整式 导航页
导航页 基础自主梳理 1.分式的基本性质 分式的分子与分母都乘(或除以)__________不等于零的整 式,分式的值__________. 这一性质可以用式子表示为𝒃 𝒂 = 𝒃·𝒎 𝒂·𝒎 , 𝒃 𝒂 = 𝒃÷𝒎 𝒂÷𝒎 (m≠0). 易错提示 m≠0是分式基本性质的一个制约条件.运用分式的基本性质 时,要注意两个“同时”:一是分式的分子与分母同时作乘法或 除法运算;二是乘(或除以)的对象必须是同一个整式. 同一个 不变

2.填空: b2 b2(2b) 2ab3 6a3b 6a3b÷(3ab- 2a2 2a 2a(2ab) 4a2b'3ab2 3ab2÷(3ab) 3.约分与最简分式 把一个分式的分子和分母的公因式约去,这种变形称为分 式的约分.分子和分母没有公因式,这样的分式称为最简分式. 温馨提示 化简分式时,一般要约去分子和分母所有的公因式,使所得 结果成为最简分式或者整式。 导航贞
导航页 2.填空: 𝒃 𝟐 𝟐𝒂 = 𝒃 𝟐 ·( ) 𝟐𝒂·( ) = 𝟐𝒂𝒃 𝟑 𝟒𝒂𝟐 𝒃 , 𝟔𝒂 𝟑 𝒃 𝟑𝒂𝒃 𝟐 = 𝟔𝒂 𝟑 𝒃÷( ) 𝟑𝒂𝒃 𝟐 ÷( ) = 𝟐𝒂 𝟐 𝒃 . 3.约分与最简分式 把一个分式的分子和分母的________约去,这种变形称为分 式的约分.分子和分母没有公因式,这样的分式称为最简分式. 温馨提示 化简分式时,一般要约去分子和分母所有的公因式,使所得 结果成为最简分式或者整式. 2ab 2ab 3ab 3ab 公因式

、9x2y32= 3yz 4.化简:(21x3y2 7x ● 导航页
导航页 4.化简:(1)-𝟗𝒙 𝟐 𝒚 𝟑 𝒛 𝟐𝟏𝒙𝟑 𝒚𝟐 =__________; (2)𝒂 𝟐-𝟒𝒂 𝟏𝟔-𝒂𝟐 =__________. - 𝟑𝒚𝒛 𝟕𝒙 - 𝒂 𝒂+𝟒

核心重难探究 知识点分式的约分 【例题】 16-a2 约分:(0n8a16 (2oaa2 12a2(a+b) 思路点拨:1)分子与分母有公因式吗?16-2可以分解为哪几 个因式的积?a2-8a+16可以分解为哪几个因式的积? (2)分子与分母有公因式吗?122(a+b)可以分解因式吗?- 16a(a2-b2)可以分解为哪几个因式的积? 导航页
导航页 核心重难探究 知识点 分式的约分 【例题】 约分:(1) 𝟏𝟔-𝒂 𝟐 𝒂𝟐-𝟖𝒂+𝟏𝟔 ; (2) 𝟏𝟐𝒂 𝟐(𝒂+𝒃) -𝟏𝟔𝒂(𝒂𝟐-𝒃 𝟐 ) . 思路点拨:(1)分子与分母有公因式吗?16-a 2可以分解为哪几 个因式的积?a 2 -8a+16可以分解为哪几个因式的积? (2)分子与分母有公因式吗?12a 2 (a+b)可以分解因式吗?- 16a(a 2 -b 2 )可以分解为哪几个因式的积?

解:1a12中1 16-a2-(a+4)(a-4)_ a+4 5(a-4)2 a-4 2 12a2(a+b)_ 4a(a+b)3a =3a -16a(a2-b2)4a(a+b)4(a-b)4(a-b) 导航页
导航页 解:(1) 𝟏𝟔-𝒂 𝟐 𝒂𝟐-𝟖𝒂+𝟏𝟔 = -(𝒂+𝟒)(𝒂-𝟒) (𝒂-𝟒) 𝟐 =- 𝒂+𝟒 𝒂-𝟒 . (2) 𝟏𝟐𝒂 𝟐(𝒂+𝒃) -𝟏𝟔𝒂(𝒂𝟐-𝒃 𝟐 ) =- 𝟒𝒂(𝒂+𝒃)·𝟑𝒂 𝟒𝒂(𝒂+𝒃)·𝟒(𝒂-𝒃) =- 𝟑𝒂 𝟒(𝒂-𝒃)

【方法归纳】 约分的关键是确定分子与分母的公因式,其一般方法是:(1) 当分子和分母都是单项式时,先找分子、分母系数的最大公 约数,再找相同字母的最低次幂;(2)当分子和分母都是多项式 时,首先要对分子、分母进行因式分解,把分子、分母变为几 个因式的积后,再找分子、分母的公因式;3)当分式的分子或 分母的系数是负数时,应先把负号提到分数线前: 导航页
导航页 【方法归纳】 约分的关键是确定分子与分母的公因式,其一般方法是:(1) 当分子和分母都是单项式时,先找分子、分母系数的最大公 约数,再找相同字母的最低次幂;(2)当分子和分母都是多项式 时,首先要对分子、分母进行因式分解,把分子、分母变为几 个因式的积后,再找分子、分母的公因式;(3)当分式的分子或 分母的系数是负数时,应先把负号提到分数线前

新知训练巩固 1.下列各式变形正确的是(C). afm b+m D 影 2.等式 a(b+1) 成立的条件是(C), a+1 (a+1)b+1) A.≠0,且b≠0 B.呋1,且b≠1 C.呋-1,且b≠-1D.,b为任意数 3.下列分式中,最简分式是(A) x2+y2 6b x2.4 D 2+4a x+y 4a x-2 a 导航页
导航页 新知训练巩固 1.下列各式变形正确的是( ). A. 𝒂 𝒃 = 𝒂+𝒎 𝒃+𝒎 B. 𝒂 𝒃 = 𝒂𝒄 𝒃𝒄 C. 𝒂𝒌 𝒃𝒌 = 𝒂 𝒃 D. 𝒂 𝒃 = 𝒂 𝟐 𝒃 𝟐 2.等式 𝒂 𝒂+𝟏 = 𝒂(𝒃+𝟏) (𝒂+𝟏)(𝒃+𝟏) 成立的条件是( ). A.a≠0,且 b≠0 B.a≠1,且 b≠1 C.a≠-1,且 b≠-1 D.a,b 为任意数 3.下列分式中,最简分式是( ). A. 𝒙 𝟐 +𝒚 𝟐 𝒙+𝒚 B. 𝟔𝒃 𝟒𝒂 C. 𝒙 𝟐-𝟒 𝒙-𝟐 D. 𝒂 𝟐 +𝟒𝒂 𝒂 C C A
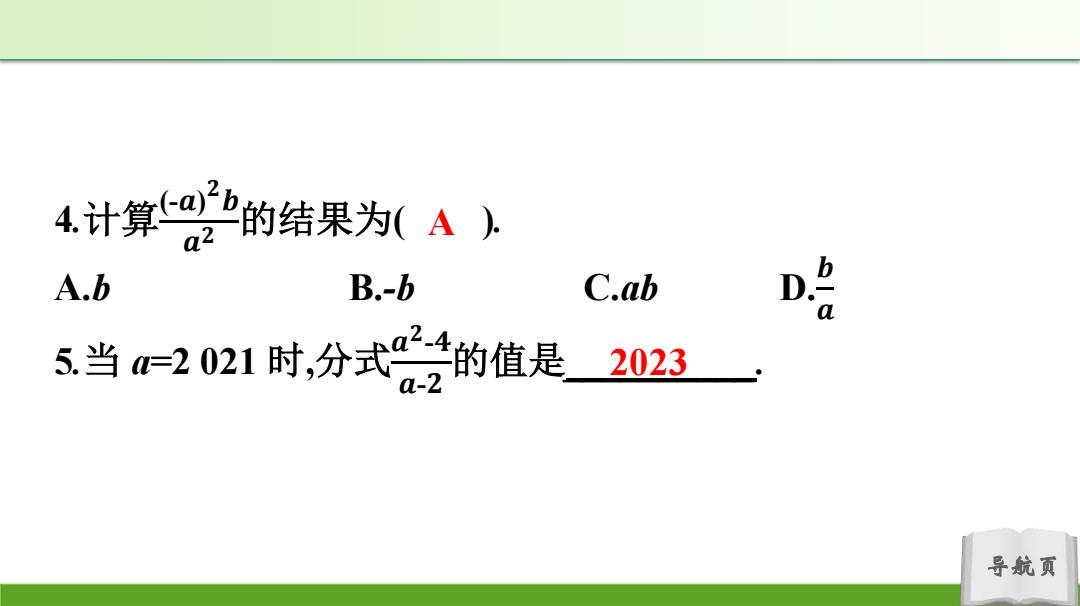
4计算a2的结果为(人上 A.b B.-b C.ab D哈 5当2021时,分式的值是2023 导航页
导航页 4.计算(-𝒂) 𝟐 𝒃 𝒂𝟐 的结果为( ). A.b B.-b C.ab D. 𝒃 𝒂 5.当 a=2 021 时,分式𝒂 𝟐-𝟒 𝒂-𝟐 的值是__________. A 2023