
家庭值亚 第1课时 一元一次不等式与一次函数的关系
第1课时 一元一次不等式与一次函数的关系

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.一元一次不等式与一次函数的关系 对于一次函数y=kc+b(0): (1)当kx+b>0时y>0,不等式x+b>0的解集就是函数y=r+b (0)的图象在x轴上方 的部分对应自变量x的取值范 围 (2)当x+b<0时,y<0,不等式c+b<0的解集就是函数 y=c+b(0)的图象在x轴下方 的部分对应自变量x的 取值范围; (3)当x+b=0时y=0,方程kc+b=0的解就是函数y=kc+b(0) 的图象与x轴交点的横坐标 导航页
导航页 基础自主梳理 1.一元一次不等式与一次函数的关系 对于一次函数y=kx+b(k≠0): (1)当kx+b>0时,y>0,不等式kx+b>0的解集就是函数y=kx+b (k≠0)的图象在x轴__________的部分对应自变量x的取值范 围; (2)当kx+b<0时,y<0,不等式kx+b<0的解集就是函数 y=kx+b(k≠0)的图象在x轴__________的部分对应自变量x的 取值范围; (3)当kx+b=0时,y=0,方程kx+b=0的解就是函数y=kx+b(k≠0) 的图象与x轴交点的__________. 上方 下方 横坐标

2.已知函数y=8x-11,要使y>0,则x应取(A) A11 8 Br0 D.x<0 导航页
导航页 2.已知函数 y=8x-11,要使 y>0,则 x 应取( ). A.x> 𝟏𝟏 𝟖 B.x0 D.x<0 A
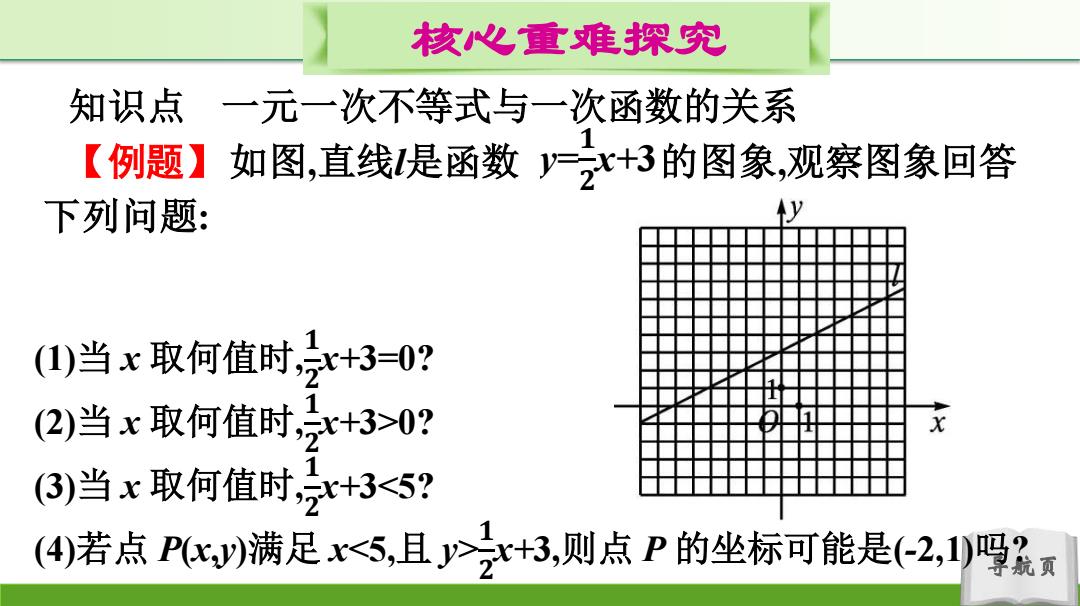
核心重难探究 知识点 一元一次不等式与一次函数的关系 【例题】如图,直线是函数一式+3的图象,观察图象回答 下列问题: (1)当x取何值时,2+3=0? (2)当x取何值时,x+3>0? (3)当x取何值时,x+3<5? (④)若点Pc)满足x5,且式+3,则点P的坐标可能是(-2,1)吗最
导航页 核心重难探究 知识点 一元一次不等式与一次函数的关系 【例题】如图,直线l是函数 的图象,观察图象回答 下列问题: y= 𝟏 𝟐 x+3 (1)当 x 取何值时, 𝟏 𝟐 x+3=0? (2)当 x 取何值时, 𝟏 𝟐 x+3>0? (3)当 x 取何值时, 𝟏 𝟐 x+3 𝟏 𝟐 x+3,则点 P 的坐标可能是(-2,1)吗?

思路点拨:本题考查一次函数、方程、不等式的关系.一次 函数的图象与x轴交点的横坐标即为第()题的解在图象上分 别找到y>0y<5的部分,求出各部分图象上所对应的x的取值范 围可得出第(2),3)题的答案对于第(4)题,由题意说明点P的横 坐标x在小于5的同时,对应的点P的位置要在直线的上方;通 过观察点(-2,1)的位置可作出判断. 导航页
导航页 思路点拨:本题考查一次函数、方程、不等式的关系.一次 函数的图象与x轴交点的横坐标即为第(1)题的解.在图象上分 别找到y>0,y<5的部分,求出各部分图象上所对应的x的取值范 围可得出第(2),(3)题的答案.对于第(4)题,由题意说明点P的横 坐标x在小于5的同时,对应的点P的位置要在直线l的上方;通 过观察点(-2,1)的位置可作出判断

解:由图象可看出函数图像与x轴的交点为(-6,0) (1)当=-6时x+3=0. 1 (2)当>-6时,x+3>0. 3)由图象可看出,当y=5时,=4,所以当<4时,x+3<5. (4)由题意,得满足点P的横坐标x<5的同时,对应的点P的位 置要在直线的上方.而点-2,1)在直线的下方,所以点P的坐标 不可能是(-2,1). 导航页
导航页 解:由图象可看出函数图像与x轴的交点为(-6,0). (1)当 x=-6 时, 𝟏 𝟐 x+3=0. (2)当 x>-6 时, 𝟏 𝟐 x+3>0. (3)由图象可看出,当 y=5 时,x=4,所以当 x<4 时, 𝟏 𝟐 x+3<5. (4)由题意,得满足点P的横坐标x<5的同时,对应的点P的位 置要在直线l的上方.而点(-2,1)在直线l的下方,所以点P的坐标 不可能是(-2,1)

【方法归纳】 根据一次函数的图象求一次方程的解、一次不等式的解集, 首先要正确画出一次函数的图象,然后确定一次函数的图象 与x轴交点的横坐标,最后确定相应方程的解或不等式的解集 导航页
导航页 【方法归纳】 根据一次函数的图象求一次方程的解、一次不等式的解集, 首先要正确画出一次函数的图象,然后确定一次函数的图象 与x轴交点的横坐标,最后确定相应方程的解或不等式的解集

新知训练巩固 1.如图,一次函数y=x+b(k>0)的图象过点(-1,0),则不等式 kc-1)+b>0的解集是(C) Ax>-2 B.x>-1 C.x>0 D.x>I 导航页
导航页 新知训练巩固 1.如图,一次函数y=kx+b(k>0)的图象过点(-1,0),则不等式 k(x-1)+b>0的解集是( ). A.x>-2 B.x>-1 C.x>0 D.x>1 C
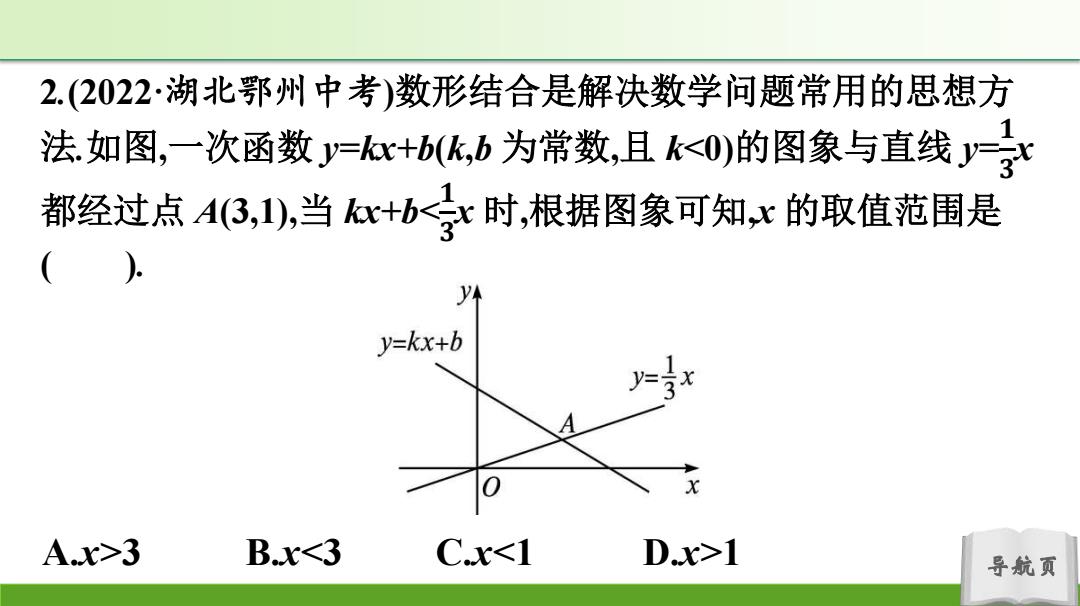
2.(2022·湖北鄂州中考)数形结合是解决数学问题常用的思想方 法.如图,一次函数x+bk,b为常数,且k0)的图象与直线宁 都经过点A3,1),当kx+b3 B.xI 导航页
导航页 2.(2022·湖北鄂州中考)数形结合是解决数学问题常用的思想方 法.如图,一次函数 y=kx+b(k,b 为常数,且 k3 B.x1