
家庭值四 第4课时 等边三角形的判定
第4课时 等边三角形的判定

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.等边三角形的判定 定理三个角都相等 的三角形是等边三角形 定理有一个角等于 60°的等腰 三角形是等 边三角形 温馨提示 1.等腰三角形中的60°角既可以是顶角,也可以是底角. 2.等边三角形包括定义在内共有三种判定方法,在实际应用 时要根据具体的已知条件选择合适的判定方法. 导航页
导航页 基础自主梳理 1.等边三角形的判定 定理 三个角都__________的三角形是等边三角形. 定理 有一个角等于__________的__________三角形是等 边三角形. 温馨提示 1.等腰三角形中的60°角既可以是顶角,也可以是底角. 2.等边三角形包括定义在内共有三种判定方法,在实际应用 时要根据具体的已知条件选择合适的判定方法. 相等 60° 等腰
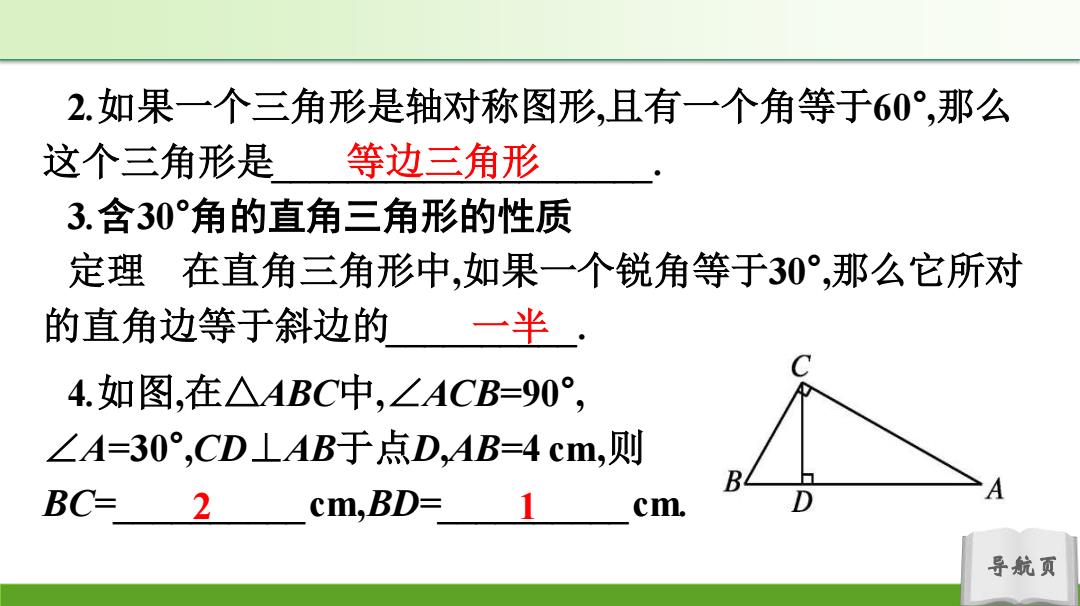
2.如果一个三角形是轴对称图形,且有一个角等于60°,那么 这个三角形是 等边三角形 3.含30°角的直角三角形的性质 定理在直角三角形中,如果一个锐角等于30°,那么它所对 的直角边等于斜边的 一半 4.如图,在△ABC中,∠ACB=90°, ∠A=30°,CD⊥AB于点D,AB=4cm,则 BC= 2 cm,BD=1 cm. 导航页
导航页 2.如果一个三角形是轴对称图形,且有一个角等于60° ,那么 这个三角形是____________________. 3.含30°角的直角三角形的性质 定理 在直角三角形中,如果一个锐角等于30° ,那么它所对 的直角边等于斜边的__________. 4.如图,在△ABC中,∠ACB=90° , ∠A=30° ,CD⊥AB于点D,AB=4 cm,则 BC=__________cm,BD=__________cm. 等边三角形 一半 2 1
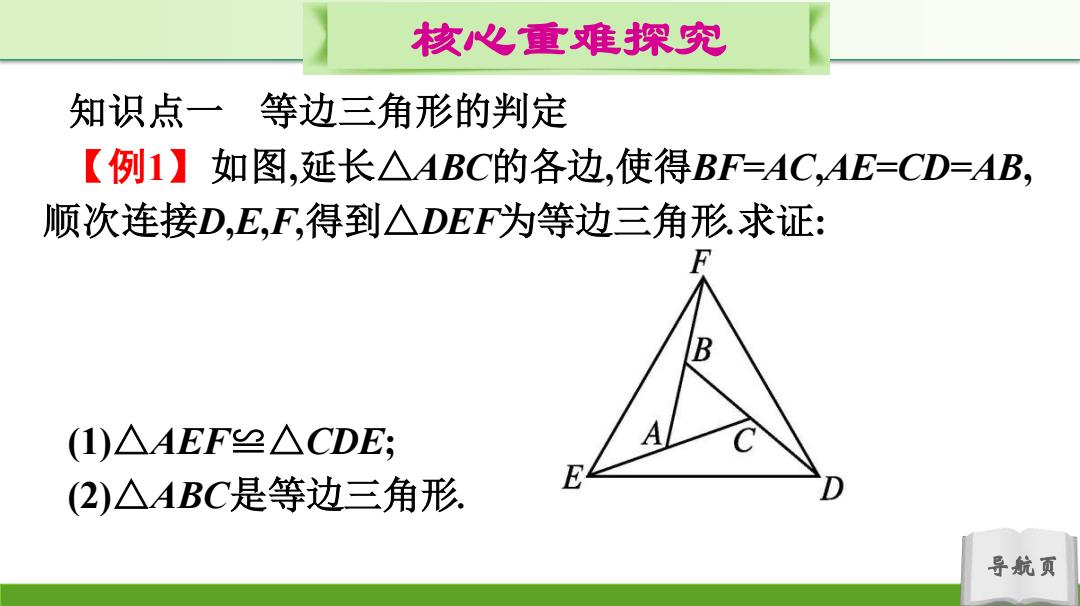
核心重难探究 知识点一等边三角形的判定 【例1】如图,延长△ABC的各边,使得BF=AC,AE=CD=AB, 顺次连接D,E,F,得到△DEF为等边三角形求证: B (1)△AEF≌△CDE; A (2)△ABC是等边三角形 导航页
导航页 核心重难探究 知识点一 等边三角形的判定 【例1】如图,延长△ABC的各边,使得BF=AC,AE=CD=AB, 顺次连接D,E,F,得到△DEF为等边三角形.求证: (1)△AEF≌△CDE; (2)△ABC是等边三角形

思路点拨:(1)需要根据AE=AB,AC=BF,证出AF=CE.再结合 已知条件即可证出△AEF≌△CDE (2)由(1)中的三角形全等,可得出∠AFE=∠CED,再结合 △DEF是等边三角形,可知∠DEF=60°,从而得出∠BAC=60°, 同理可得∠ACB=60°,那么∠ABC=60°.因而△ABC是等边三 角形. 导航页
导航页 思路点拨:(1)需要根据AE=AB,AC=BF,证出AF=CE.再结合 已知条件即可证出△AEF≌△CDE. (2)由(1)中的三角形全等,可得出∠AFE=∠CED,再结合 △DEF是等边三角形,可知∠DEF=60° ,从而得出∠BAC=60° , 同理可得∠ACB=60° ,那么∠ABC=60° .因而△ABC是等边三 角形

证明:(1)·BF=AC,AB=AE, .AF-CE. :△DEF是等边三角形, ..EF-DE. 又AE=CD, .·△AEF≌△CDE. 导航页
导航页 证明:(1)∵BF=AC,AB=AE, ∴AF=CE. ∵△DEF是等边三角形, ∴EF=DE. 又∵AE=CD, ∴△AEF≌△CDE

2)由△AEF≌△CDE,得∠EFA=∠DEC △DEF是等边三角形, .·∠DEF=60°. ..∠DEC+∠FEC=60°. .&∠EFA+∠FEC=60° .·∠BAC=∠EFA+∠FEC=60°. 同理可得∠ACB=60°. .·∠BAC=∠ACB=∠ABC=60°. ,:△ABC是等边三角形. 导航页
导航页 (2)由△AEF≌△CDE,得∠EFA=∠DEC. ∵△DEF是等边三角形, ∴∠DEF=60° . ∴∠DEC+∠FEC=60° . ∴∠EFA+∠FEC=60° . ∴∠BAC=∠EFA+∠FEC=60° . 同理可得∠ACB=60° . ∴∠BAC=∠ACB=∠ABC=60° . ∴△ABC是等边三角形

【方法归纳】 等边三角形的判定方法的选择 (1)若已知三边关系,则考虑运用等边三角形的定义进行判 定 (2)若已知三角关系,则根据“三个角都相等的三角形是等边 三角形”进行判定 (3)若已知该三角形是等腰三角形,则可再寻找一个内角等 于60°即可. 导航页
导航页 【方法归纳】 等边三角形的判定方法的选择 (1)若已知三边关系,则考虑运用等边三角形的定义进行判 定. (2)若已知三角关系,则根据“三个角都相等的三角形是等边 三角形”进行判定. (3)若已知该三角形是等腰三角形,则可再寻找一个内角等 于60°即可
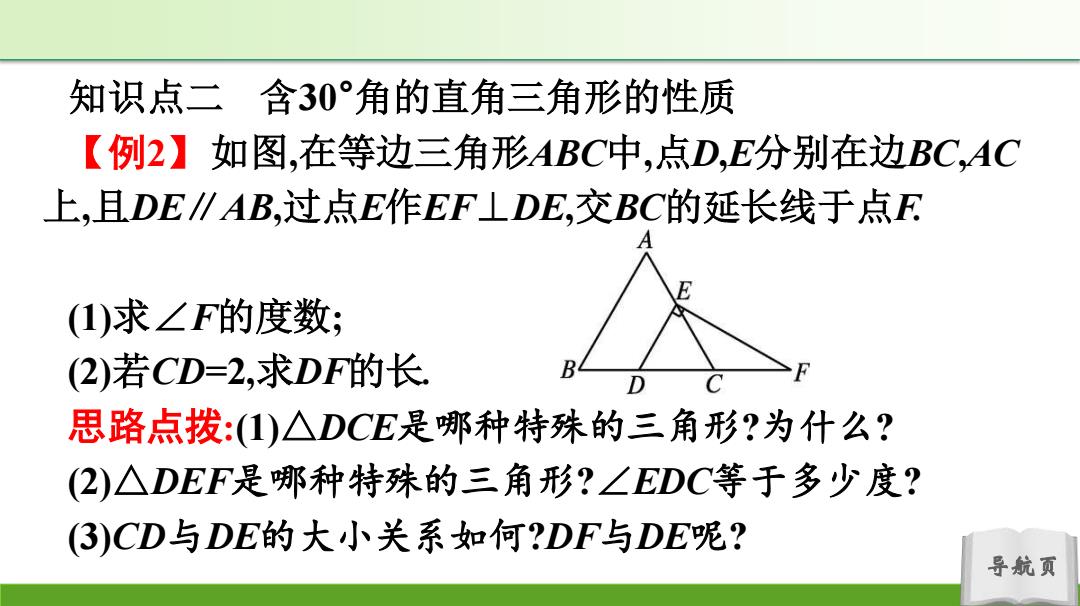
知识点二含30°角的直角三角形的性质 【例2】如图,在等边三角形ABC中,点D,E分别在边BC,AC 上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F (1)求∠F的度数; (2)若CD=2,求DF的长 B D C 思路点拨:(1)△DCE是哪种特殊的三角形?为什么? (2)△DEF是哪种特殊的三角形?∠EDC等于多少度? 3)CD与DE的大小关系如何?DF与DE呢? 导航页
导航页 知识点二 含30°角的直角三角形的性质 【例2】如图,在等边三角形ABC中,点D,E分别在边BC,AC 上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F. (1)求∠F的度数; (2)若CD=2,求DF的长. 思路点拨:(1)△DCE是哪种特殊的三角形?为什么? (2)△DEF是哪种特殊的三角形?∠EDC等于多少度? (3)CD与DE的大小关系如何?DF与DE呢?