
家庭值亚 第3课时 等腰三角形的判定与反证法
第3课时 等腰三角形的判定与反证法

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固
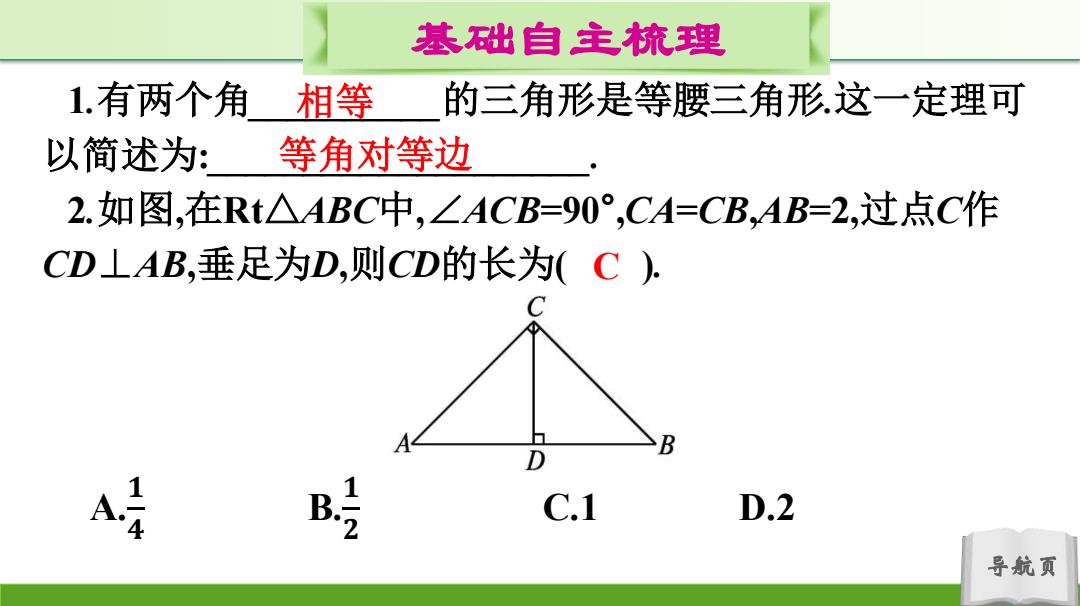
基础自主梳理 1.有两个角 相等 的三角形是等腰三角形这一定理可 以简述为: 等角对等边 2.如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=2,过点C作 CD⊥AB,垂足为D,则CD的长为(C) A B D A B C.1 D.2 导航页
导航页 基础自主梳理 1.有两个角__________的三角形是等腰三角形.这一定理可 以简述为:____________________. 2.如图,在Rt△ABC中,∠ACB=90° ,CA=CB,AB=2,过点C作 CD⊥AB,垂足为D,则CD的长为( ). A. 𝟏 𝟒 B. 𝟏 𝟐 C.1 D.2 相等 等角对等边 C

3.满足下列条件的三角形:①内角比为12,1;②内角比为 2,2,5;③内角比为1.1,1;④内角比为123,其中是等 腰三角形的有①②③.(填序号) 4.反证法 在证明时,先假设命题的结论不成立,然后推导出与定 义、基本事实、已有定理或已知条件相矛盾的结果,从而证 明命题的结论一定成立这种证明方法称为反证法: 导航页
导航页 3.满足下列条件的三角形:①内角比为1∶2∶1;②内角比为 2∶2∶5;③内角比为1∶1∶1;④内角比为1∶2∶3,其中是等 腰三角形的有__________.(填序号) 4.反证法 在证明时,先假设命题的结论__________,然后推导出与定 义、基本事实、已有定理或已知条件相矛盾的结果,从而证 明命题的结论一定成立.这种证明方法称为反证法. ①②③ 不成立

5.用反证法证明“一个三角形中不能有两个角是钝角”,我们 可先假设这个三角形中有两个角是钝角,与之相矛盾 的定理是三角形内角和定理 导航页
导航页 5.用反证法证明“一个三角形中不能有两个角是钝角”,我们 可先假设________________________________,与之相矛盾 的定理是______________________________. 这个三角形中有两个角是钝角 三角形内角和定理

核心重难探究 知识点 等腰三角形的判定 【例题】如图,在△ABC中,点D,E分别在边AC,AB上, BD=CE,∠DBC=∠ECB. E 求证:AB=AC B 思路点拨:(1)条件“BD=CE”与“∠DBC=∠ECB”中涉及的边、 角分别在哪两个三角形中?这两个三角形全等吗? (2)∠ABC与∠ACB分别在哪两个三角形中?它们相等吗 导航页
导航页 核心重难探究 知识点 等腰三角形的判定 【例题】 如图,在△ABC中,点D,E分别在边AC,AB上, BD=CE,∠DBC=∠ECB. 求证:AB=AC. 思路点拨:(1)条件“BD=CE”与“∠DBC=∠ECB”中涉及的边、 角分别在哪两个三角形中?这两个三角形全等吗? (2)∠ABC与∠ACB分别在哪两个三角形中?它们相等吗?

证明:·BD=CE,∠DBC=∠ECB,BC=CB, .·△BCE≌△CBD .·∠ABC=∠ACB. ..AB=AC. 导航页
导航页 证明:∵BD=CE,∠DBC=∠ECB,BC=CB, ∴△BCE≌△CBD. ∴∠ABC=∠ACB. ∴AB=AC

【方法归纳】 1.等腰三角形的判定方法“等角对等边”是证明两条线段相 等的重要方式之一,当所要证明相等的两条线段(或与之相等 的相关线段)在同一个三角形中,即可考虑运用该判定方法进 行证明. 导航页
导航页 【方法归纳】 1.等腰三角形的判定方法“等角对等边”是证明两条线段相 等的重要方式之一,当所要证明相等的两条线段(或与之相等 的相关线段)在同一个三角形中,即可考虑运用该判定方法进 行证明

2.构造等腰三角形的“三个方法” (1)“角平分线+平行线”构造等腰三角形,应用平行线的性质 得到角的相等关系,应用“等角对等边”得到边相等 (2)“角平分线+垂线”构造等腰三角形,逆用等腰三角形的 “三线合一”的性质 3)利用“三角形中角的2倍关系”构造等腰三角形 导航页
导航页 2.构造等腰三角形的“三个方法” (1)“角平分线+平行线”构造等腰三角形,应用平行线的性质 得到角的相等关系,应用“等角对等边”得到边相等. (2)“角平分线+垂线”构造等腰三角形,逆用等腰三角形的 “三线合一”的性质. (3)利用“三角形中角的2倍关系”构造等腰三角形

新知训练巩固 1.如图,在△ABC中,AB=AC,∠C=72°,BC=V5,以点B为圆心,BC 为半径画弧,交AC于点D,则线段AD的长为(C). B A.22 B.2V3 C.V5 D.√6 导航页
导航页 新知训练巩固 1.如图,在△ABC 中,AB=AC,∠C=72°,BC= 𝟓,以点 B 为圆心,BC 为半径画弧,交 AC 于点 D,则线段 AD 的长为( ). A.2 𝟐 B.2 𝟑 C. 𝟓 D. 𝟔 C