
家庭缠四 第2课时 直角三角形全等的判定
第2课时 直角三角形全等的判定

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.直角三角形全等的判定 定理斜边 和一条直角边分别相等的两个直角三 角形全等可以简述为“斜边、直角边”或“HL 99 2.下列条件中,不能判定两个直角三角形全等的是(D). A.斜边和一锐角分别对应相等 B.两条直角边分别对应相等 C.一条直角边与斜边分别对应相等 D.两锐角对应相等 导航页
导航页 基础自主梳理 1.直角三角形全等的判定 定理__________和一条__________分别相等的两个直角三 角形全等.可以简述为“斜边、直角边”或“__________” . 2.下列条件中,不能判定两个直角三角形全等的是( ). A.斜边和一锐角分别对应相等 B.两条直角边分别对应相等 C.一条直角边与斜边分别对应相等 D.两锐角对应相等 斜边 直角边 HL D
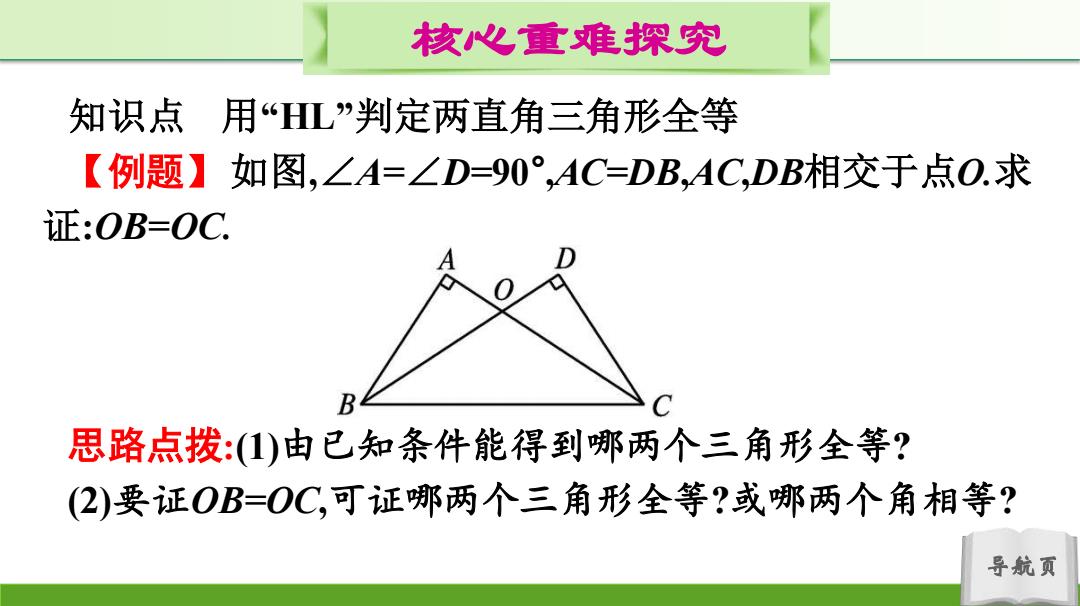
核心重难探究 知识点 用“HL”判定两直角三角形全等 【例题】如图,∠A=∠D=0°,AC=DB,AC,DB相交于点O.求 证:OB=OC 思路点拨:(1)由已知条件能得到哪两个三角形全等? (2)要证OB=OC,可证哪两个三角形全等?或哪两个角相等? 导航页
导航页 核心重难探究 知识点 用“HL”判定两直角三角形全等 【例题】 如图,∠A=∠D=90° ,AC=DB,AC,DB相交于点O.求 证:OB=OC. 思路点拨:(1)由已知条件能得到哪两个三角形全等? (2)要证OB=OC,可证哪两个三角形全等?或哪两个角相等?

证法一:·∠A=∠D=90°,AC=DB,BC=CB, .:Rt△ABC≌Rt△DCB(HL). .·∠OBC=∠OCB..OB=OC 证法二:·∠A=∠D=90°,AC=DB,BC=CB, ,,Rt△ABC≌Rt△DCBH) ..AB=DC. 叉.'∠AOB=∠DOC, .·△ABO≌△DCO(AAS): ..OB=OC. 导航页
导航页 证法一:∵∠A=∠D=90° ,AC=DB,BC=CB, ∴Rt△ABC≌Rt△DCB(HL). ∴∠OBC=∠OCB.∴OB=OC. 证法二:∵∠A=∠D=90° ,AC=DB,BC=CB, ∴Rt△ABC≌Rt△DCB(HL). ∴AB=DC. 又∵∠AOB=∠DOC, ∴△ABO≌△DCO(AAS). ∴OB=OC

【方法归纳】 判定直角三角形全等的方法: (1)若有一组直角边和斜边分别相等,则用HL”进行判定 (2)若有一组锐角和斜边分别相等,则用“AAS”判定 3)若有一组锐角和一组直角边分别相等:①若直角边是锐 角的对边,则用“AAS”判定;②若直角边是锐角的邻边,则用 “ASA”判定 (4)若有两组直角边分别相等,则用SAS”判定 导航页
导航页 【方法归纳】 判定直角三角形全等的方法: (1)若有一组直角边和斜边分别相等,则用“HL”进行判定. (2)若有一组锐角和斜边分别相等,则用“AAS”判定. (3)若有一组锐角和一组直角边分别相等:①若直角边是锐 角的对边,则用“AAS”判定;②若直角边是锐角的邻边,则用 “ASA”判定. (4)若有两组直角边分别相等,则用“SAS”判定
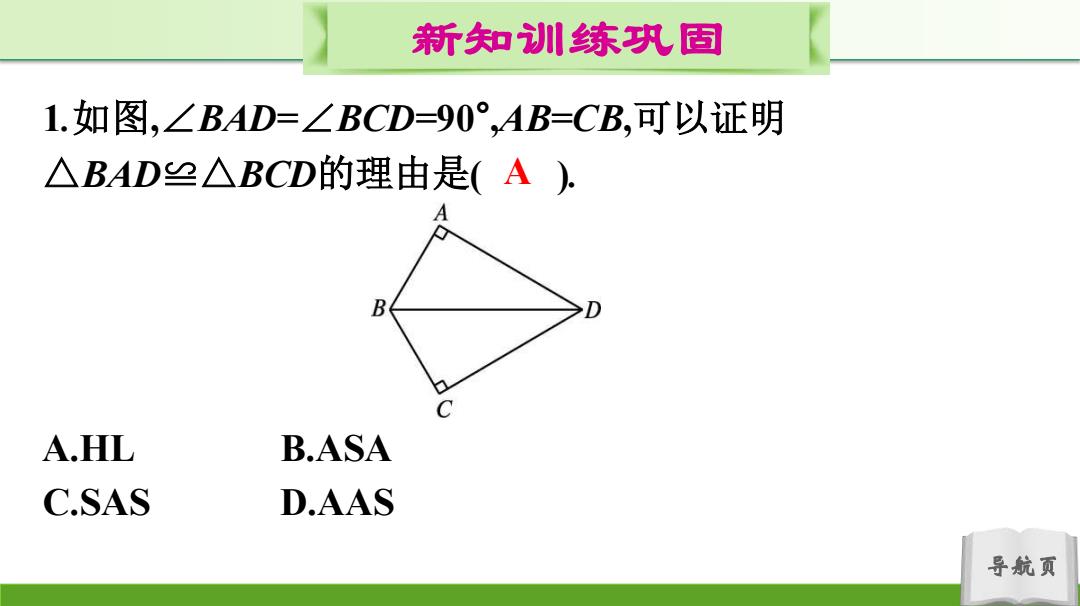
新知训练巩固 1.如图,∠BAD=∠BCD=90°,AB=CB,可以证明 △BAD≌△BCD的理由是(A). B A.HL B.ASA C.SAS D.AAS 导航页
导航页 新知训练巩固 1.如图,∠BAD=∠BCD=90° ,AB=CB,可以证明 △BAD≌△BCD的理由是( ). A.HL B.ASA C.SAS D.AAS A

2.如图,在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E.若 ∠B=28°,则∠AEC等于( )B E B D A.28°B.59°C.60°D.62° 导航页
导航页 2.如图,在△ABC中,∠C=90° ,AD=AC,DE⊥AB交BC于点E.若 ∠B=28° ,则∠AEC等于( ). A.28°B.59° C.60° D.62° B
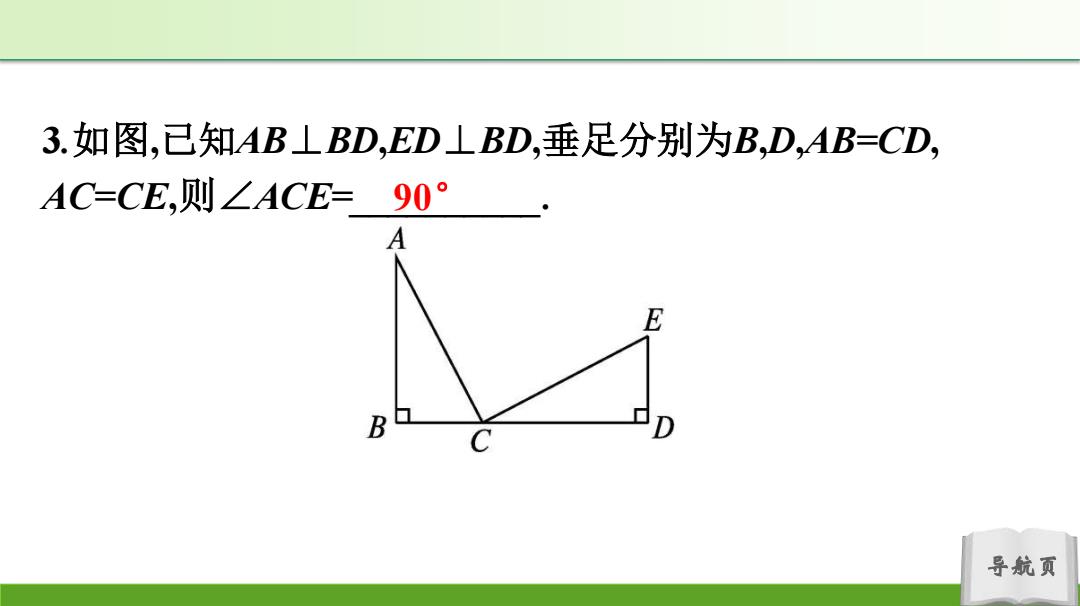
3.如图,已知AB⊥BD,ED⊥BD,垂足分别为B,D,AB=CD, AC=CE,则∠ACE=90° E B 导航页
导航页 3.如图,已知AB⊥BD,ED⊥BD,垂足分别为B,D,AB=CD, AC=CE,则∠ACE=__________. 90°

4.如图,在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC, 垂足分别为点E,F,且DE=DF 求证:△ABC是等边三角形 证明:·AB=AC,.·∠B=∠C ·DE⊥AB,DF⊥BC B .·∠DEA=∠DFC=90°. :D为AC的中点,DA=DC 又:DE=DF,.Rt△ADE≌Rt△CDFHL). .·∠A=∠C..·∠A=∠B=∠C.,·△ABC是等边三角形 导航页
导航页 4.如图,在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC, 垂足分别为点E,F,且DE=DF. 求证:△ABC是等边三角形. 证明 :∵AB=AC,∴∠B=∠C. ∵DE⊥AB,DF⊥BC. ∴∠DEA=∠DFC=90° . ∵D为AC的中点,∴DA=DC. 又∵DE=DF,∴Rt△ADE≌Rt△CDF(HL). ∴∠A=∠C.∴∠A=∠B=∠C.∴△ABC是等边三角形