
家庭你亚 第1课时 直角三角形的性质与判定
第1课时 直角三角形的性质与判定

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固
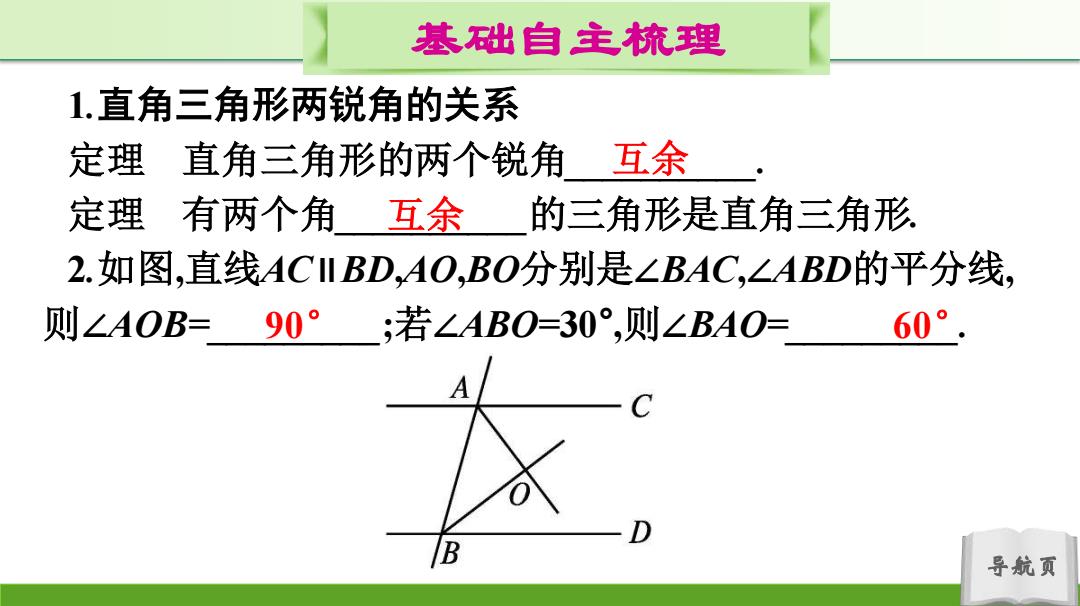
基础自主梳理 1.直角三角形两锐角的关系 定理直角三角形的两个锐角 互余 定理有两个角互余 的三角形是直角三角形 2.如图,直线ACII BD,AO,BO分别是∠BAC,∠ABD的平分线, 则∠AOB=90·;若∠ABO=30°,则∠BAO= 60°. D 导航页
导航页 基础自主梳理 1.直角三角形两锐角的关系 定理 直角三角形的两个锐角__________. 定理 有两个角__________的三角形是直角三角形. 2.如图,直线AC∥BD,AO,BO分别是∠BAC,∠ABD的平分线, 则∠AOB=_________;若∠ABO=30° ,则∠BAO=_________. 互余 互余 90° 60°

3.勾股定理及其逆定理 勾股定理 直角三角形两条直角边的平方和等于斜边的 平方 勾股定理的逆定理 如果三角形两边的 平方和等于第 三边的平方,那么这个三角形是直角三角形, 4.在直角三角形中,若勾为3,股为4,则弦为〔A) A.5 B.6 C.7 D.8 5.在△ABC中,AB=12,BC=9,则当AC=15或3√万时,△ABC 是直角三角形. 导航页
导航页 3.勾股定理及其逆定理 勾股定理 直角三角形两条直角边的平方和等于斜边的 __________. 勾股定理的逆定理 如果三角形两边的__________等于第 三边的平方,那么这个三角形是直角三角形. 4.在直角三角形中,若勾为3,股为4,则弦为( ). A.5 B.6 C.7 D.8 5.在△ABC中,AB=12,BC=9,则当AC=__________时,△ABC 是直角三角形. 平方 平方和 A 15 或 3 𝟕

6.互逆命题与互逆定理 ()互逆命题在两个命题中,如果一个命题的条件和结论 分别是另一个命题的结论 和 条件,那么这两个 命题称为互逆命题,其中一个命题称为另一个命题的逆命题, (2)互逆定理如果一个定理的逆命题经过证明是 真命题,那么它也是一个定理,其中一个定理称为另一个 定理的逆定理 7.命题:“如果m是整数,那么它是有理数”,则它的逆命题为 如果m是有理数,那么它是整数 导航页
导航页 6.互逆命题与互逆定理 (1)互逆命题 在两个命题中,如果一个命题的条件和结论 分别是另一个命题的__________和__________,那么这两个 命题称为互逆命题,其中一个命题称为另一个命题的逆命题. (2)互逆定理 如果一个定理的逆命题经过证明是 __________,那么它也是一个定理,其中一个定理称为另一个 定理的逆定理. 7.命题:“如果m是整数,那么它是有理数”,则它的逆命题为 ________________________________. 结论 条件 真命题 如果m是有理数,那么它是整数

核心重难探究 知识点 勾股定理及其逆定理 【例题】如图,在四边形ABCD中,∠C=90°,AB=13,BC=4, CD=3,AD=12. B 1)求证:AD⊥BD; 2)求四边形ABCD的面积. 思路点拨:(1)BD的长是多少?△ABD是什么三角形? 2)四边形ABCD的面积为哪两个三角形的面积之和? 导航页
导航页 核心重难探究 知识点 勾股定理及其逆定理 【例题】 如图,在四边形ABCD中,∠C=90° ,AB=13,BC=4, CD=3,AD=12. (1)求证:AD⊥BD; (2)求四边形ABCD的面积. 思路点拨:(1)BD的长是多少?△ABD是什么三角形? (2)四边形ABCD的面积为哪两个三角形的面积之和?

(1)证明:在Rt△BCD中,由勾股定理,得 BD=VBC2+CD2=V42+32=5. 在△ABD中,BD=5,AB=13,AD=12, 则AD2+BD2=122+52=169=132=AB2, 即AD2+BD2=AB2. 由勾股定理的逆定理知,△ABD是直角三角形,且∠ADB=0°, 即AD⊥BD. (2)解:四边形ABCD的面积为 1 Sa4BD+SABCD-2×12×5+2X3×4=30+6=36. 导航页
导航页 (1)证明 :在Rt△BCD中,由勾股定理,得 BD= 𝑩𝑪𝟐 + 𝑪𝑫𝟐 = 𝟒𝟐 + 𝟑𝟐 =5. 在△ABD中,BD=5,AB=13,AD=12, 则AD2+BD2=122+5 2=169=132=AB2 , 即AD2+BD2=AB2 . 由勾股定理的逆定理知,△ABD是直角三角形,且∠ADB=90° , 即AD⊥BD. (2)解:四边形ABCD的面积为 S△ABD+S△BCD= 𝟏 𝟐 ×12×5+ 𝟏 𝟐 ×3×4=30+6=36

【方法归纳】 1.涉及直角三角形中的求边长问题,通常用到勾股定理当图 形中涉及等边三角形和等腰直角三角形时,除注意有关性质 的应用外,还要注意轴对称等性质的灵活应用. 2.勾股定理的逆定理常用来判定三角形是直角三角形,其最 长边所对的角为直角 导航页
导航页 【方法归纳】 1.涉及直角三角形中的求边长问题,通常用到勾股定理.当图 形中涉及等边三角形和等腰直角三角形时,除注意有关性质 的应用外,还要注意轴对称等性质的灵活应用. 2.勾股定理的逆定理常用来判定三角形是直角三角形,其最 长边所对的角为直角
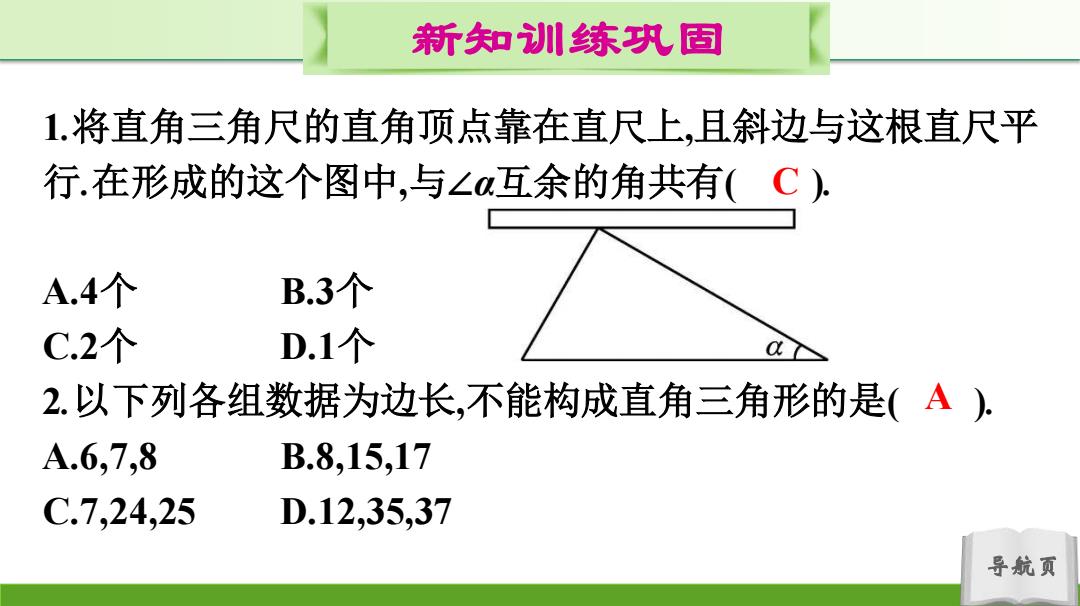
新知训练巩固 1.将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平 行.在形成的这个图中,与∠互余的角共有( A.4个 B.3个 C.2个 D.1个 a 2.以下列各组数据为边长,不能构成直角三角形的是(A), A.6,7,8 B.8,15,17 C.7,24,25 D.12,35,37 导航页
导航页 新知训练巩固 1.将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平 行.在形成的这个图中,与∠α互余的角共有( ). A.4个 B.3个 C.2个 D.1个 2.以下列各组数据为边长,不能构成直角三角形的是( ). A.6,7,8 B.8,15,17 C.7,24,25 D.12,35,37 C A

3.下列命题中,其逆命题是真命题的是(B) A.对顶角相等 B.两直线平行,同位角相等 C全等三角形的对应角相等 D.正方形的四个角都相等 4.如图,等边三角形OAB的边长为2,则点B的坐标为(D) A x A.(1,1) B.W3,1) C.3,5) D.1,V3) 导航页
导航页 3. 下列命题中,其逆命题是真命题的是( ). A.对顶角相等 B.两直线平行,同位角相等 C.全等三角形的对应角相等 D.正方形的四个角都相等 4.如图,等边三角形OAB的边长为2,则点B的坐标为( ). B D A.(1,1) B.( 𝟑,1) C.( 𝟑, 𝟑) D.(1, 𝟑)