
家庭猴四 第2课时 一元一次不等式组的解法(2)
第2课时 一元一次不等式组的解法(2)

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固
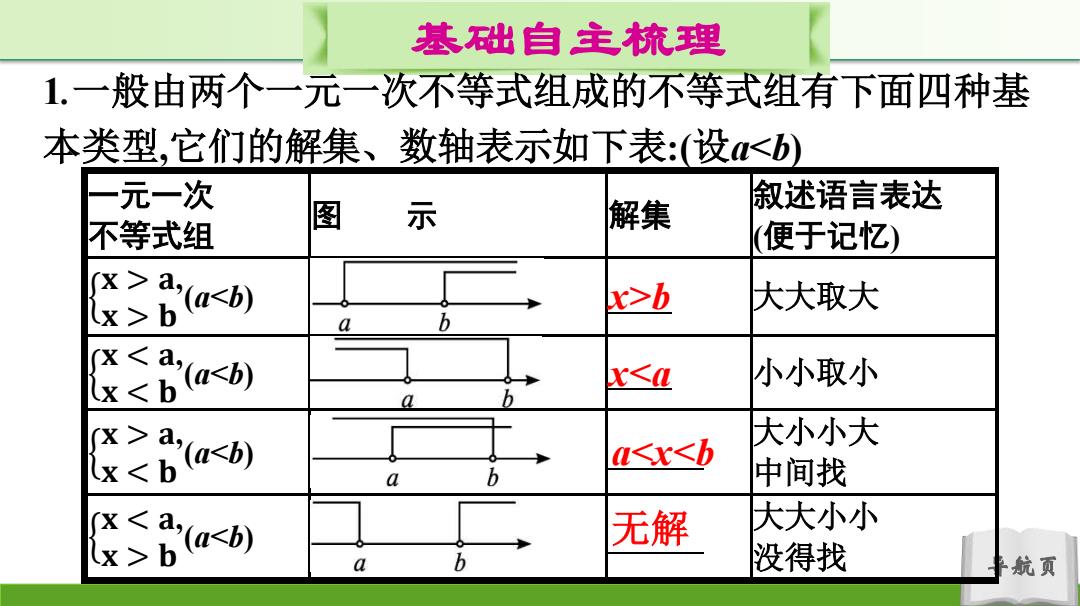
基础自主梳理 1.一般由两个一元一次不等式组成的不等式组有下面四种基 本类型,它们的解集、数轴表示如下表:(设b 大大取大 a b harl x≤4 小小取小 a b 之barj 大小小大 M≤x≤b a b 中间找 ash 无解 大大小小 a b 没得找 航页
导航页 基础自主梳理 1.一般由两个一元一次不等式组成的不等式组有下面四种基 本类型,它们的解集、数轴表示如下表:(设a 𝐚, 𝐱 > 𝐛 (a 𝐚, 𝐱 𝐛 (ab x<a a<x<b 无解

2.求下列各不等式组的解集,并在数轴上表示出来 >2Q2S之 解:(1)012345→,所以原不等式组的解集为心4. (2) 012345 ,所以原不等式组的解集为x<2. (3)012345,所以原不等式组的解集为2<x<4. (4) 012345→,所以原不等式组无解 导航页
导航页 2.求下列各不等式组的解集,并在数轴上表示出来. (1) 𝒙 > 𝟒, 𝒙 > 𝟐; (2) 𝒙 𝟐; (4) 𝒙 > 𝟒, 𝒙 4. (2) ,所以原不等式组的解集为 x<2. (3) ,所以原不等式组的解集为 2<x<4. (4) ,所以原不等式组无解

核心重难探究 知识点 由不等式(组)的解确定字母的取值范围 5x+2>3(x-1), 【例题】已知关于x的不等式组1 x≤8-2x+2a 3 有四个整 数解,求实数a的取值范围。 思路点拨:先求得不等式组的解集,再借助数轴或口诀对照 所给的解集,确定的取值范围. 导航页
导航页 核心重难探究 知识点 由不等式(组)的解确定字母的取值范围 【例题】已知关于x的不等式组 有四个整 数解,求实数a的取值范围. 𝟓𝒙 + 𝟐 > 𝟑(𝒙-𝟏), 𝟏 𝟐 𝒙 ≤ 𝟖- 𝟑 𝟐 𝒙 + 𝟐𝒂 思路点拨:先求得不等式组的解集,再借助数轴或口诀对照 所给的解集,确定a的取值范围

5x+2>3(x-1),① 解5x≤8-2x+2a.② 解不等式①,得心 解不等式②,得x≤a+4. 由不等式组有四个整数解,得1≤a十4<2, 所以-3≤<-2. 导航页
导航页 解: 𝟓𝒙 + 𝟐 > 𝟑(𝒙-𝟏),① 𝟏 𝟐 𝒙 ≤ 𝟖- 𝟑 𝟐 𝒙 + 𝟐𝒂.② 解不等式①,得 x>- 𝟓 𝟐 . 解不等式②,得x≤a+4. 由不等式组有四个整数解,得1≤a+4<2, 所以-3≤a<-2

【方法归纳】 解决含有参数的不等式(组)问题,一般需按以下步骤进行: (1)先求出不等式(组)的解集(可含有参数); (2)借助于数轴,形象准确地把握不等式(组)有解、无解以及 有几个整数解的问题; (3)注意端点值,这类问题一般都与端点有关,一是用数轴来 说明是哪个端点,二是进行检验,有无端点满足题意,进而最终 确定参数的取值范围 导航页
导航页 【方法归纳】 解决含有参数的不等式(组)问题,一般需按以下步骤进行: (1)先求出不等式(组)的解集(可含有参数); (2)借助于数轴,形象准确地把握不等式(组)有解、无解以及 有几个整数解的问题; (3)注意端点值,这类问题一般都与端点有关,一是用数轴来 说明是哪个端点,二是进行检验,有无端点满足题意,进而最终 确定参数的取值范围
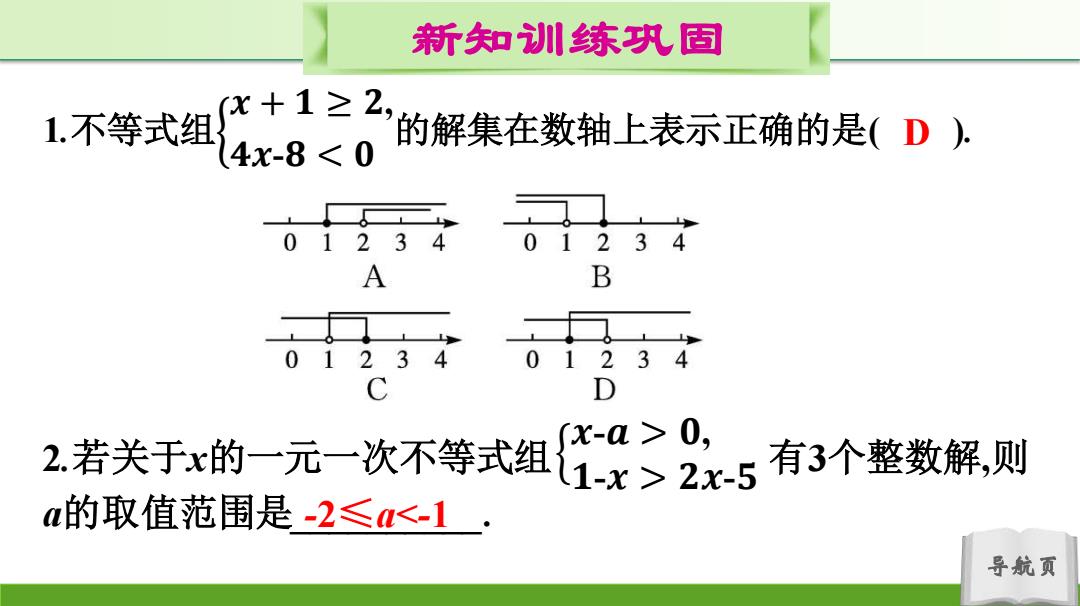
新知训练巩固 1.不等式组 化+1≥2, 4x-8≤0 的解集在数轴上表示正确的是(D), 01234 01234 A B 。对 01234 D 2,若关于x的一元一次不等式组>2x5有3个整数解,则 x-a>0, a的取值范围是-2≤a<-1 导航页
导航页 新知训练巩固 1.不等式组 𝒙 + 𝟏 ≥ 𝟐, 𝟒𝒙-𝟖 𝟎, 𝟏-𝒙 > 𝟐𝒙-𝟓 -2≤a<-1

路漫漫其修远兮 吾将上下而求索
路漫漫其修远兮 吾将上下而求索