
家庭你四 第2课时 三角形三边的垂直平分线
第2课时 三角形三边的垂直平分线

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.三角形三边的垂直平分线 三角形三条边的垂直平分线相交于一点,并且这一点 到三个顶点的距离相等 2.已知△ABC的三条边的垂直平分线的交点在△ABC的边 上,则△ABC的形状为(B). A锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定 导航页
导航页 基础自主梳理 1.三角形三边的垂直平分线 三角形三条边的垂直平分线相交于__________,并且这一点 到三个顶点的距离__________. 2.已知△ABC的三条边的垂直平分线的交点在△ABC的边 上,则△ABC的形状为( ). A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定 一点 相等 B

3.过一点作直线的垂线 条件作法 图示 (1)以P为圆心,任意长为半径画弧,交直线1于点 米C A,B; 点P在 直线l上 (2)分别以A,B为圆心,大于AB的长为半径画 AP 弧,两弧交于点C; 3)作直线PC (1)以P为圆心画弧,使弧与直线I交于点A,B; 点P在 (2)分别以A,B为圆心,大于AB的长为半径画弧, 直线1外 两弧交于点C; B (3)作直线PC
导航页 3.过一点作直线l的垂线 条 件 作 法 图示 点 P 在 直线l上 (1)以 P 为圆心,任意长为半径画弧,交直线 l 于点 A,B; (2)分别以 A,B 为圆心,大于𝟏 𝟐 AB 的长为半径画 弧,两弧交于点 C; (3)作直线 PC 点 P 在 直线l外 (1)以 P 为圆心画弧,使弧与直线 l 交于点 A,B; (2)分别以A,B为圆心,大于𝟏 𝟐 AB的长为半径画弧, 两弧交于点 C; (3)作直线 PC

温馨提示 在直线上得到两点A,B后,上述作法就是用尺规作一条线段 的垂直平分线的方法步骤了,这也是一种基本的尺规作图,应 熟练掌握 导航页
导航页 温馨提示 在直线l上得到两点A,B后,上述作法就是用尺规作一条线段 的垂直平分线的方法步骤了,这也是一种基本的尺规作图,应 熟练掌握

4.已知等腰三角形的底边及底边上的高,能画出 一个 三角形;已知三角形的一边及这边上的高,能画出无数个 三角形 导航页
导航页 4.已知等腰三角形的底边及底边上的高,能画出________个 三角形;已知三角形的一边及这边上的高,能画出________个 三角形. 一 无数

核心重难探究 知识点 三角形三边的垂直平分线 【例题】某社区要修建一处公共服务设施,使它到三个公 寓A,B,C的距离相等 A C B (1)三个公寓A,B,C的位置如图,请你在图中确定这处公共服 务设施(用点P表示)的位置; (2)若∠BAC=66°,则∠BPC的度数是多少? 导航页
导航页 核心重难探究 知识点 三角形三边的垂直平分线 【例题】某社区要修建一处公共服务设施,使它到三个公 寓A,B,C的距离相等. (1)三个公寓A,B,C的位置如图,请你在图中确定这处公共服 务设施(用点P表示)的位置; (2)若∠BAC=66° ,则∠BPC的度数是多少?

思路点拨:)到不在同一条直线上的三点距离相等的点有 何特征?如何确定? (2)在(1)中所作的图形中存在哪些等腰三角形?∠ABC与 ∠ACB的和是多少?∠PBA与∠PCA的和呢? 导航页
导航页 思路点拨:(1)到不在同一条直线上的三点距离相等的点有 何特征?如何确定? (2)在(1)中所作的图形中存在哪些等腰三角形?∠ABC与 ∠ACB的和是多少?∠PBA与∠PCA的和呢?
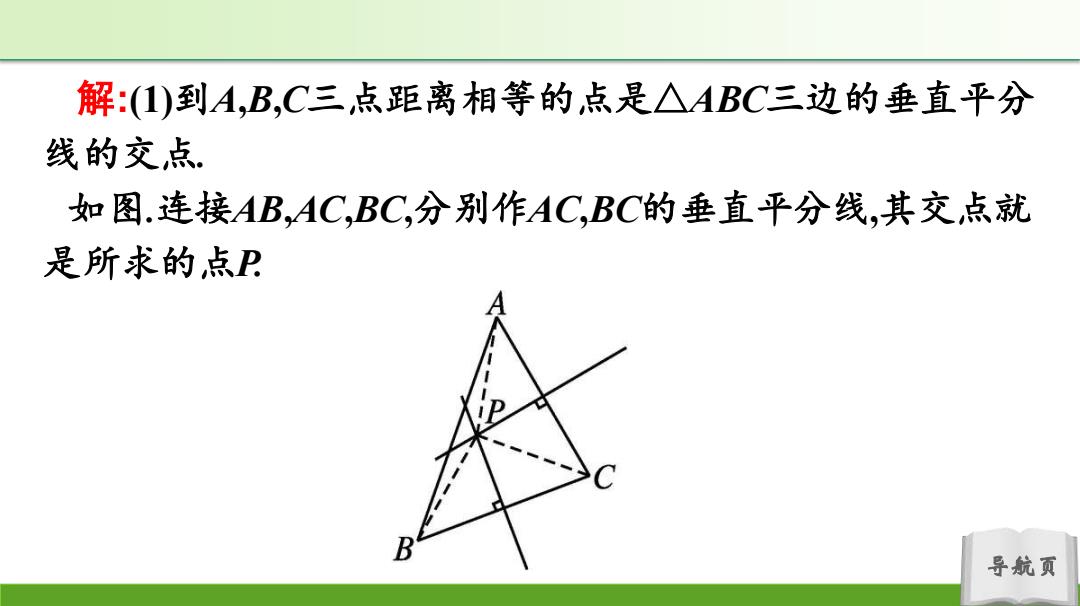
解:(1)到A,B,C三点距离相等的点是△ABC三边的垂直平分 线的交点 如图.连接AB,AC,BC,分别作AC,BC的垂直平分线,其交点就 是所求的,点P 导航页
导航页 解:(1)到A,B,C三点距离相等的点是△ABC三边的垂直平分 线的交点. 如图.连接AB,AC,BC,分别作AC,BC的垂直平分线,其交点就 是所求的点P

(2)由线段的垂直平分线性质,得PA=PB=PC .'∠BAP=∠ABP,∠PAC=∠PCA,∠PBC=∠PCB. :∠BAC=66°,.∠BAP+∠PAC=66°. .∠ABP+∠ACP=66°. 而∠ABC+∠ACB=180°-66°=114°, .∠PBC+∠PCB=114°-(∠ABP+∠ACP =114°-66°=48°. .∠BPC=180°-(∠PBC+∠PCB)=180°-48°=132°. 导航页
导航页 (2)由线段的垂直平分线性质,得PA=PB=PC. ∴∠BAP=∠ABP,∠PAC=∠PCA,∠PBC=∠PCB. ∵∠BAC=66° ,∴∠BAP+∠PAC=66° . ∴∠ABP+∠ACP=66° . 而∠ABC+∠ACB=180°-66° =114° , ∴∠PBC+∠PCB=114°-(∠ABP+∠ACP) =114°-66° =48° . ∴∠BPC=180°-(∠PBC+∠PCB)=180°-48° =132°