
家庭作业 第2课时 等腰三角形的其他性质 与等边三角形的性质
第2课时 等腰三角形的其他性质 与等边三角形的性质

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.等腰三角形的其他性质 等腰三角形两底角的平分线, 相等,两腰上的中线 相等,两腰上的高相等 知识拓展 由面积法容易得到如下结论:等腰三角形底边上任意一点到 两腰的距离和等于一腰上的高 导航页
导航页 基础自主梳理 1.等腰三角形的其他性质 等腰三角形两底角的平分线__________,两腰上的中线 __________,两腰上的高__________. 知识拓展 由面积法容易得到如下结论:等腰三角形底边上任意一点到 两腰的距离和等于一腰上的高. 相等 相等 相等

2.等边三角形的性质 等边三角形的三个内角都相等 ,并且每个角都等于 60° 温馨提示 等边三角形是一种特殊的等腰三角形,它具有等腰三角形的 一切性质,等边三角形也是轴对称图形,有3条对称轴。 导航页
导航页 2.等边三角形的性质 等边三角形的三个内角都__________,并且每个角都等于 __________. 温馨提示 等边三角形是一种特殊的等腰三角形,它具有等腰三角形的 一切性质,等边三角形也是轴对称图形,有3条对称轴. 相等 60°
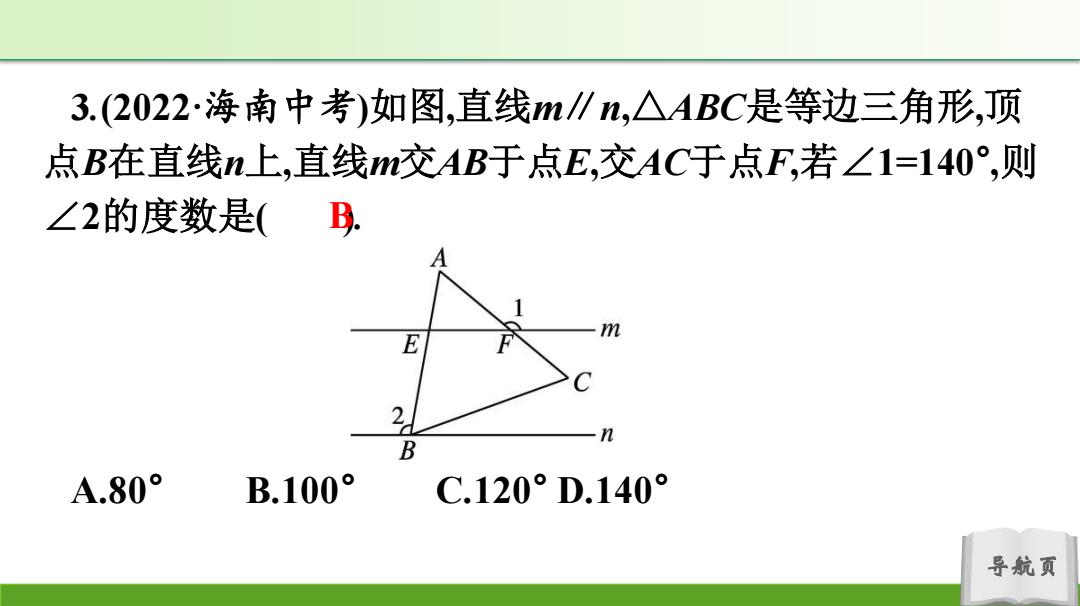
3.(2022·海南中考)如图,直线m∥n,△ABC是等边三角形,顶 点B在直线n上,直线m交AB于点E,交AC于点F,若∠1=140°,则 ∠2的度数是(B. m E B A.80° B.100° C.120°D.140° 导航页
导航页 3.(2022·海南中考)如图,直线m∥n,△ABC是等边三角形,顶 点B在直线n上,直线m交AB于点E,交AC于点F,若∠1=140° ,则 ∠2的度数是( ). A.80° B.100° C.120° D.140° B
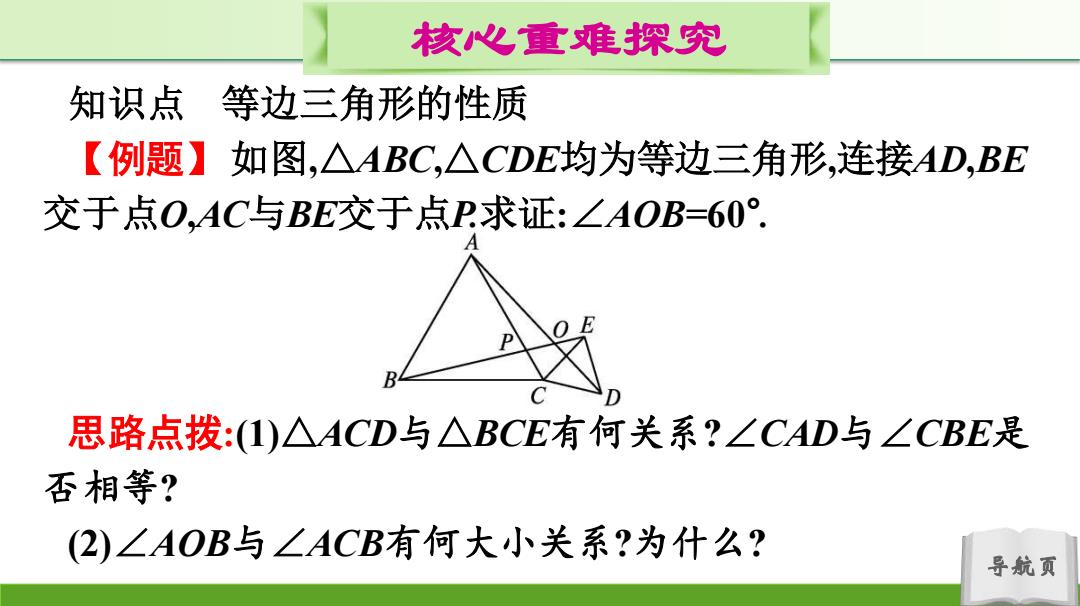
核心心重难探究 知识点 等边三角形的性质 【例题】如图,△ABC,△CDE均为等边三角形,连接AD,BE 交于点O,AC与BE交于点P求证:∠AOB=60°. 思路点拨:(1)△ACD与△BCE有何关系?∠CAD与∠CBE是 否相等? (2)∠AOB与∠ACB有何大小关系?为什么? 导航页
导航页 核心重难探究 知识点 等边三角形的性质 【例题】 如图,△ABC,△CDE均为等边三角形,连接AD,BE 交于点O,AC与BE交于点P.求证:∠AOB=60° . 思路点拨:(1)△ACD与△BCE有何关系?∠CAD与∠CBE是 否相等? (2)∠AOB与∠ACB有何大小关系?为什么?

证明:·“△ABC和△ECD都是等边三角形, .·AC=BC,CD=CE,∠ACB=∠DCE=60°. .·∠ACB+∠ACE=∠DCE+∠ACE, 即∠BCE=∠ACD. 在△ACD和△BCE中, ·'AC=BC,∠ACD=∠BCE,CD=CE, .·△ACD≌△BCE..·∠CAD=∠CBE. .∠APO=∠BPC, .·∠AOP=∠BCP=60°,即∠AOB=60°. 导航页
导航页 证明:∵△ABC和△ECD都是等边三角形, ∴AC=BC,CD=CE,∠ACB=∠DCE=60° . ∴∠ACB+∠ACE=∠DCE+∠ACE, 即∠BCE=∠ACD. 在△ACD和△BCE中, ∵AC=BC,∠ACD=∠BCE,CD=CE, ∴△ACD≌△BCE.∴∠CAD=∠CBE. ∵∠APO=∠BPC, ∴∠AOP=∠BCP=60° ,即∠AOB=60°

【方法归纳】 正确地利用等边三角形中隐含的条件证明全等是解决本题 的关键若当条件中已知边求角的度数时,要考虑应用“等边对 等角”将边相等转化为角相等;当出现等边三角形求角的度数 时,要想到应用“等边三角形的每个内角都等于60°”. 导航页
导航页 【方法归纳】 正确地利用等边三角形中隐含的条件证明全等是解决本题 的关键.若当条件中已知边求角的度数时,要考虑应用“等边对 等角”将边相等转化为角相等;当出现等边三角形求角的度数 时,要想到应用“等边三角形的每个内角都等于60°”

新知训练织固 1.下列说法不正确的是(C) A.等腰三角形两腰上的中线相等 B.等腰三角形两底角的平分线相等 C等腰三角形的高、中线、角平分线互相重合 D.等边三角形同一条边上的高、中线互相重合 导航页
导航页 新知训练巩固 1.下列说法不正确的是( ). A.等腰三角形两腰上的中线相等 B.等腰三角形两底角的平分线相等 C.等腰三角形的高、中线、角平分线互相重合 D.等边三角形同一条边上的高、中线互相重合 C

2.如图,在△PAB中,PA=PB,M,N,K分别是边PA,PB,AB上的点, 且AM=BK,BN=AK若∠MKN=44°,则∠P的度数为(D), M A.44°B.66° C.88°D.92° A K 3.如图,在等边三角形ABC中,点D是边 BC的中点,则∠BAD=30° B D 导航页
导航页 2.如图,在△PAB中,PA=PB,M,N,K分别是边PA,PB,AB上的点, 且AM=BK,BN=AK.若∠MKN=44° ,则∠P的度数为( ). A.44°B.66° C.88°D.92° 3.如图,在等边三角形ABC中,点D是边 BC的中点,则∠BAD=__________. D 30°