
家庭你亚 第1课时 线段的垂直平分线的定理
第1课时 线段的垂直平分线的定理

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.线段垂直平分线的性质与判定 定理线段垂直平分线上的点到这条线段两个端点的距离 相等 定理到一条线段两个端点距离相等的点,在这条线段的 垂直平分线上 导航页
导航页 基础自主梳理 1.线段垂直平分线的性质与判定 定理 线段垂直平分线上的点到这条线段两个端点的距离 __________. 定理 到一条线段两个端点距离相等的点,在这条线段的 __________上. 相等 垂直平分线

温馨提示 1.线段是轴对称图形,线段的垂直平分线是线段的一条对称 轴. 2.线段垂直平分线的性质定理与判定定理是互逆定理运用 判定定理判定一条直线是某线段的垂直平分线时,应找到与 这条线段的两个端,点距离相等的两个点才行 导航页
导航页 温馨提示 1.线段是轴对称图形,线段的垂直平分线是线段的一条对称 轴. 2.线段垂直平分线的性质定理与判定定理是互逆定理.运用 判定定理判定一条直线是某线段的垂直平分线时,应找到与 这条线段的两个端点距离相等的两个点才行
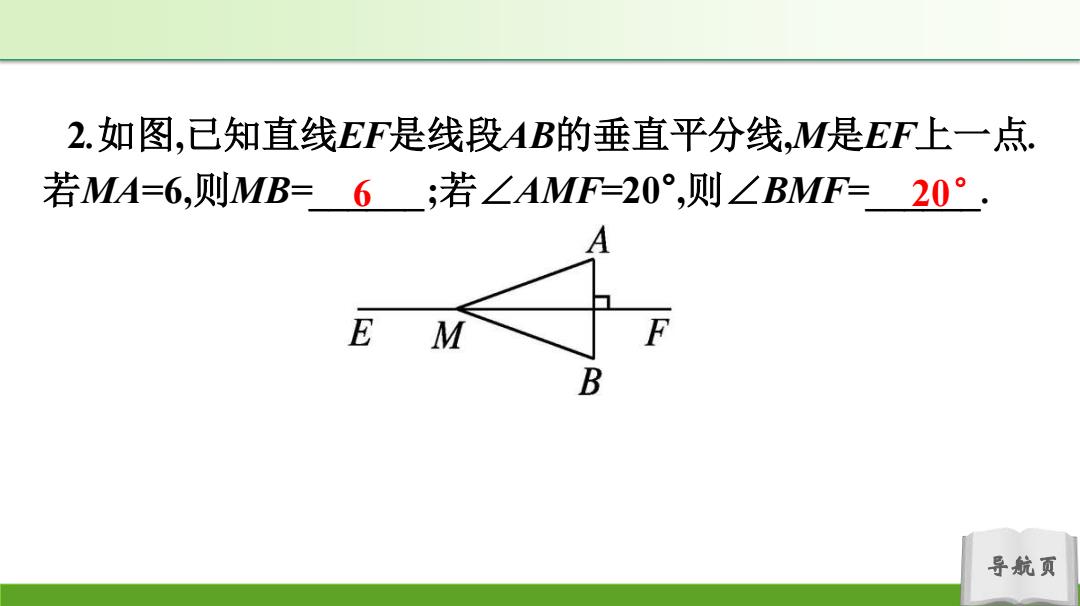
2.如图,已知直线EF是线段AB的垂直平分线,M是EF上一点 若MA=6,则MB=6;若∠AMF=20°,则∠BMF=20°. A E M B 导航页
导航页 2.如图,已知直线EF是线段AB的垂直平分线,M是EF上一点. 若MA=6,则MB=______ 6 ;若∠AMF=20° ,则∠BMF=______. 20°
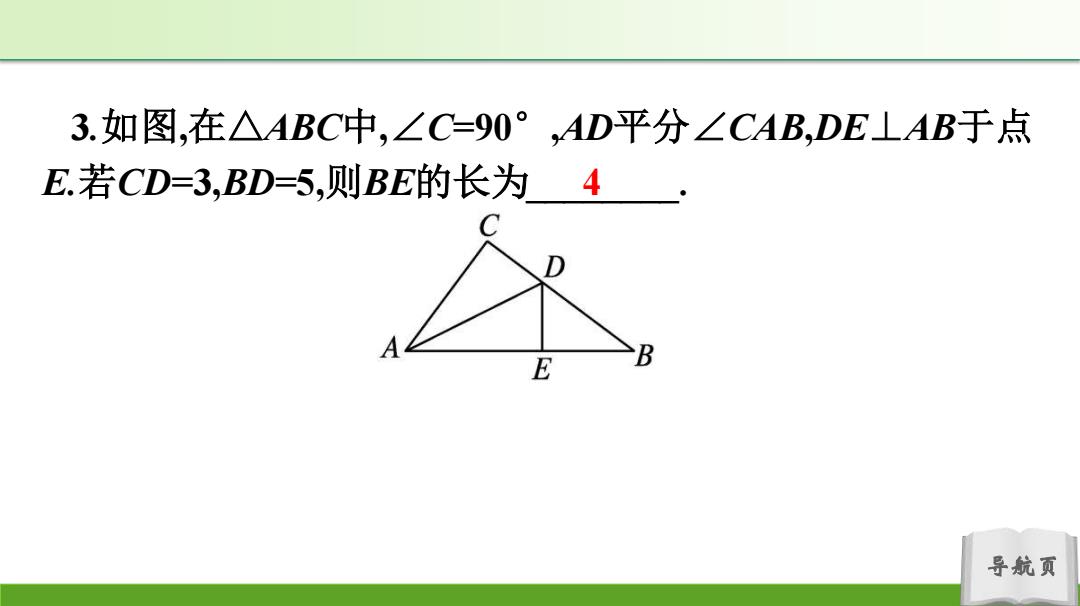
3.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点 E.若CD=3,BD=5,则BE的长为4 E B 导航页
导航页 3.如图,在△ABC中,∠C=90° ,AD平分∠CAB,DE⊥AB于点 E.若CD=3,BD=5,则BE的长为____4____
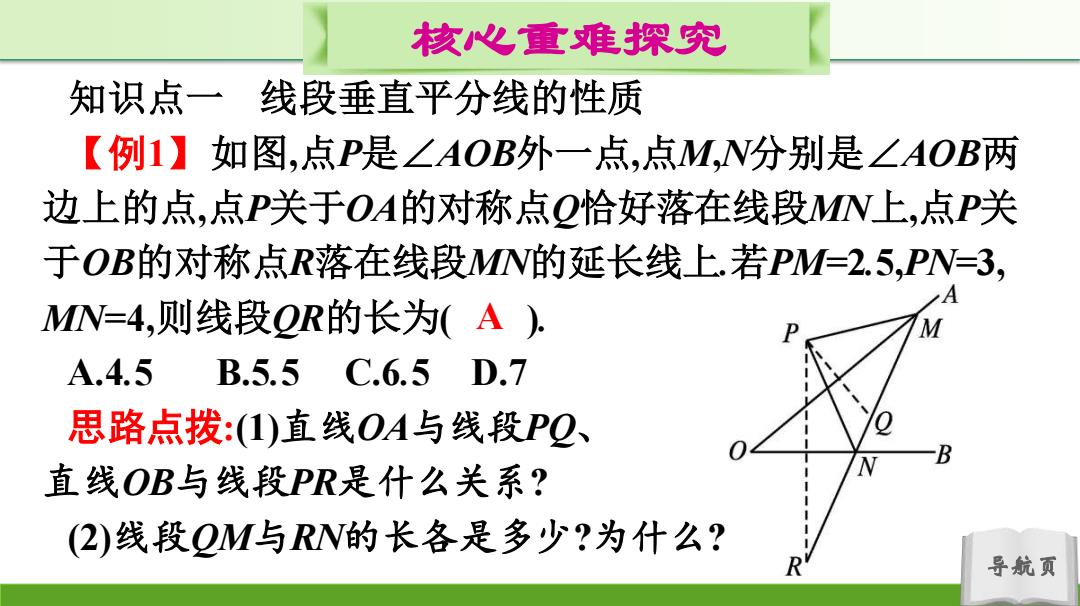
核心重难探究 知识点一线段垂直平分线的性质 【例1】如图,点P是∠AOB外一点,点M,N分别是∠AOB两 边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关 于OB的对称点R落在线段MN的延长线上.若PM=2.5,PN=3, MN=4,则线段QR的长为A): M A.4.5 B.5.5 C.6.5D.7 思路点拨:(1)直线OA与线段PQ、 直线OB与线段PR是什么关系? (2)线段QM与RN的长各是多少?为什么? 导航页
导航页 核心重难探究 知识点一 线段垂直平分线的性质 【例1】如图,点P是∠AOB外一点,点M,N分别是∠AOB两 边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关 于OB的对称点R落在线段MN的延长线上.若PM=2.5,PN=3, MN=4,则线段QR的长为( ). A.4.5 B.5.5 C.6.5 D.7 思路点拨:(1)直线OA与线段PQ、 直线OB与线段PR是什么关系? (2)线段QM与RN的长各是多少?为什么? A

【方法归纳】 线段的垂直平分线是证明线段相等的重要依据之一.在应用 时,要注意分清条件与结论,防止混淆.在含有线段垂直平分线 的图形中,含有全等三角形但在应用时,一般不用三角形全等 的方法来解决,因为应用线段垂直平分线的性质可使解题过 程更为简捷借助线段垂直平分线的性质解决问题,有时需要 作辅助线,其方法是连接线段的端点和垂直平分线上的已知 点. 导航页
导航页 【方法归纳】 线段的垂直平分线是证明线段相等的重要依据之一.在应用 时,要注意分清条件与结论,防止混淆.在含有线段垂直平分线 的图形中,含有全等三角形.但在应用时,一般不用三角形全等 的方法来解决,因为应用线段垂直平分线的性质可使解题过 程更为简捷.借助线段垂直平分线的性质解决问题,有时需要 作辅助线,其方法是连接线段的端点和垂直平分线上的已知 点
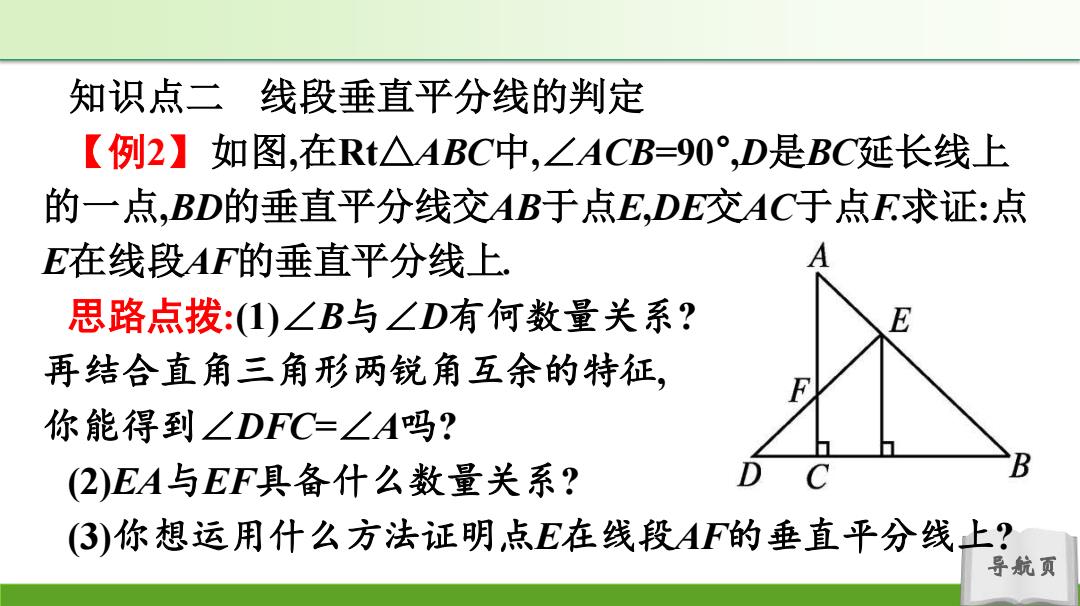
知识点二线段垂直平分线的判定 【例2】如图,在Rt△ABC中,∠ACB=90°,D是BC延长线上 的一点,BD的垂直平分线交AB于点E,DE交AC于点F求证:点 E在线段AF的垂直平分线上 思路点拨:(1)∠B与∠D有何数量关系? E 再结合直角三角形两锐角互余的特征, 你能得到∠DFC=∠A吗? (2)EA与EF具备什么数量关系? 3)你想运用什么方法证明,点E在线段AF的垂直平分线上? 导航页
导航页 知识点二 线段垂直平分线的判定 【例2】如图,在Rt△ABC中,∠ACB=90° ,D是BC延长线上 的一点,BD的垂直平分线交AB于点E,DE交AC于点F.求证:点 E在线段AF的垂直平分线上. 思路点拨:(1)∠B与∠D有何数量关系? 再结合直角三角形两锐角互余的特征, 你能得到∠DFC=∠A吗? (2)EA与EF具备什么数量关系? (3)你想运用什么方法证明点E在线段AF的垂直平分线上?

证明:·点E在线段BD的垂直平分线上, .ED=EB..·∠B=∠D :‘∠ACB=90°, .·∠A+∠B=90°,∠D+∠DFC=90°. .:∠DFC=∠A. 又·∠DFC=∠AFE, .·∠AFE=∠A..·EA=EF ,·点E在线段AF的垂直平分线上 导航页
导航页 证明:∵点E在线段BD的垂直平分线上, ∴ED=EB.∴∠B=∠D. ∵∠ACB=90° , ∴∠A+∠B=90° ,∠D+∠DFC=90° . ∴∠DFC=∠A. 又∵∠DFC=∠AFE, ∴∠AFE=∠A.∴EA=EF. ∴点E在线段AF的垂直平分线上