
家庭缠四 第1课时 '”旋转的概念与性质
第1课时 旋转的概念与性质

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.旋转的概念 在平面内,将一个图形绕一个定点按某个方向 转动一 个角度,这样的图形运动称为旋转,这个定点称为 旋转中心,转动的角称为旋转角.旋转不改变图形的 形状 和大小 2.在日常生活中,我们经常见到以下情景:①钟表指针的转动; ②汽车方向盘的转动;③打气筒打气时,活塞的运动;④传送带 上瓶装饮料的移动.其中属于旋转的是 ①②.(填序号) 导航页
导航页 基础自主梳理 1.旋转的概念 在平面内,将一个图形绕一个定点按某个__________转动一 个__________,这样的图形运动称为旋转,这个定点称为 __________,转动的角称为__________.旋转不改变图形的 __________和__________. 2.在日常生活中,我们经常见到以下情景:①钟表指针的转动; ②汽车方向盘的转动;③打气筒打气时,活塞的运动;④传送带 上瓶装饮料的移动.其中属于旋转的是__________.(填序号) 方向 角度 旋转中心 旋转角 形状 大小 ①②

3.旋转的性质 一个图形和它经过旋转所得的图形中,对应点到旋转中心的 距离相等,任意一组对应点与旋转中心的连线所成的 角都等于旋转角;对应线段相等,对应角相等 导航页
导航页 3.旋转的性质 一个图形和它经过旋转所得的图形中,对应点到旋转中心的 距离__________,任意一组对应点与旋转中心的连线所成的 角都等于__________;对应线段__________,对应角_________. 相等 旋转角 相等 相等
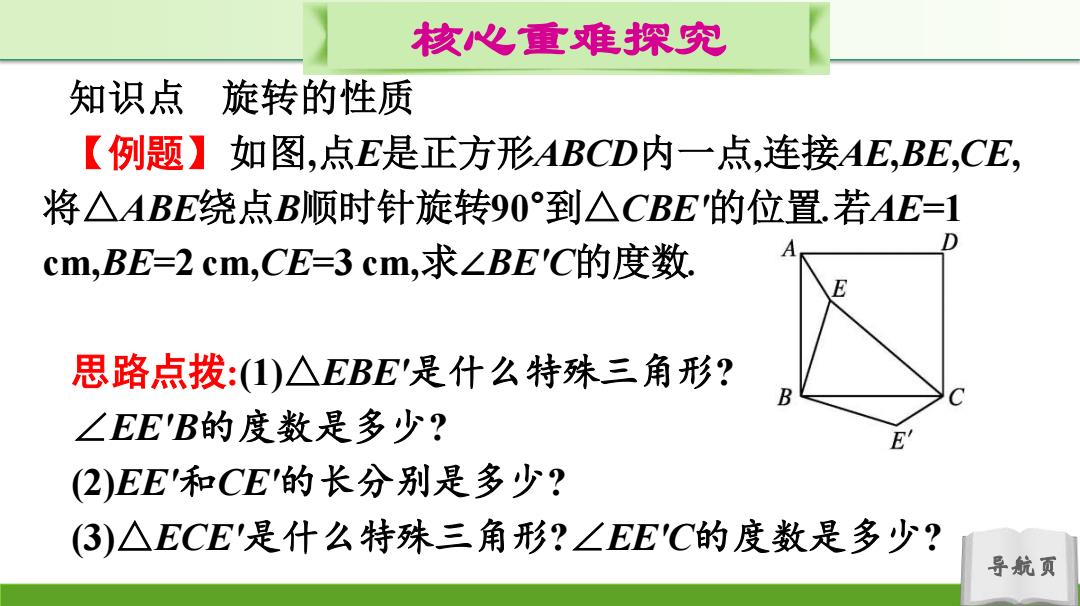
核心重难探究 知识点 旋转的性质 【例题】如图,点E是正方形ABCD内一点,连接AE,BE,CE, 将△ABE绕点B顺时针旋转90°到△CBE的位置.若AE=1 D cm,BE=2cm,CE=3cm,求∠BE'C的度数 思路点拨:(1)△EBE是什么特殊三角形? B ∠EE'B的度数是多少? (2)EE'和CE的长分别是多少? 3)△ECE'是什么特殊三角形?∠EEC的度数是多少? 导航页
导航页 核心重难探究 知识点 旋转的性质 【例题】如图,点E是正方形ABCD内一点,连接AE,BE,CE, 将△ABE绕点B顺时针旋转90°到△CBE'的位置.若AE=1 cm,BE=2 cm,CE=3 cm,求∠BE'C的度数. 思路点拨:(1)△EBE'是什么特殊三角形? ∠EE'B的度数是多少? (2)EE'和CE'的长分别是多少? (3)△ECE'是什么特殊三角形?∠EE'C的度数是多少?

解:连接EE',由旋转的性质可知,CE'=AE=1cm,BE=BE=2cm, ∠EBE=∠ABC=90°,则∠BE'E=45° 由勾股定理,得EE'=√BE2+BE2=V22+2z=2V2(cm) ·12+(2V2)2=32,即CE2+EE2=CE2, .·△ECE'是直角三角形,∠EE'C=90°. .·∠BEC=∠BE'E+∠EE'C=45°+90°=135°. 导航页
导航页 解:连接EE',由旋转的性质可知,CE'=AE=1 cm,BE'=BE=2 cm, ∠EBE'=∠ABC=90° ,则∠BE'E=45° . 由勾股定理,得 EE'= 𝑩𝑬𝟐 + 𝑩𝑬' 𝟐 = 𝟐𝟐 + 𝟐𝟐 =2 𝟐(cm). ∵1 2 +(2 𝟐) 2 =3 2 ,即 CE'2 +E'E2 =CE2 , ∴△ECE'是直角三角形,∠EE'C=90° . ∴∠BE'C=∠BE'E+∠EE'C=45°+90° =135°

【方法归纳】 旋转的性质的基本应用 (1)证明线段或角相等 ①根据旋转角相等,对应点与旋转中心的连线相等可得线段 相等或角相等. ②根据旋转前后的图形全等,可得图形的对应线段相等,对 应角相等 (2)计算图形的面积、线段的长度或角的大小 导航页
导航页 【方法归纳】 旋转的性质的基本应用 (1)证明线段或角相等. ①根据旋转角相等,对应点与旋转中心的连线相等可得线段 相等或角相等. ②根据旋转前后的图形全等,可得图形的对应线段相等,对 应角相等. (2)计算图形的面积、线段的长度或角的大小

新知训川练巩固 1.下列运动属于旋转的是(C). A.滚动过程中的篮球的滚动 B.风筝在空中飘动 C钟表的钟摆的摆动 D.一个图形沿某条直线对折的过程 导航页
导航页 新知训练巩固 1.下列运动属于旋转的是( ). A.滚动过程中的篮球的滚动 B.风筝在空中飘动 C.钟表的钟摆的摆动 D.一个图形沿某条直线对折的过程 C

2.如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过 变换得到Rt△ODE.若点C的坐标为0,1),AC=2,则这种变换可 以是(A) A.△ABC绕点C顺时针旋转0°,再向下平移3个单位长度 B.△ABC绕点C顺时针旋转0°,再向下平移1个单位长度 C.△ABC绕点C逆时针旋转0°,再向下平移1个单位长度 D.△ABC绕点C逆时针旋转0°,再向下平移3个单位长度 导航页
导航页 2.如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过 变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可 以是( ). A.△ABC绕点C顺时针旋转90° ,再向下平移3个单位长度 B.△ABC绕点C顺时针旋转90° ,再向下平移1个单位长度 C.△ABC绕点C逆时针旋转90° ,再向下平移1个单位长度 D.△ABC绕点C逆时针旋转90° ,再向下平移3个单位长度 A

3.如图,将△ABC绕点A逆时针旋转55°得到△ADE,若 ∠E=70°且AD⊥BC于点F,则∠BAC的度数为C). E B A.65 B.70° C.75° D.80° 导航页
导航页 3.如图,将△ABC绕点A逆时针旋转55°得到△ADE,若 ∠E=70°且AD⊥BC于点F,则∠BAC的度数为( ). A.65° B.70° C.75° D.80° C