
家庭值亚 第1课时 平行四边形的边和角的性质
第1课时 平行四边形的边和角的性质

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.平行四边形的概念与表示 两组对边分别平行 的四边形叫做平行四边形.平行四 边形不相邻的两个顶点连成的线段叫做它的对角线如图,四 边形ABCD是平行四边形,记作口ABCD,读作平行四边形ABCD 线段BD就是ABCD的一条对角线 2.平行四边形的对称性 平行四边形是, 中心 对称图形,两条对角线的交点是它 的对称中心 导航页
导航页 基础自主梳理 1.平行四边形的概念与表示 两组对边分别__________的四边形叫做平行四边形.平行四 边形不相邻的两个顶点连成的线段叫做它的对角线.如图,四 边形ABCD是平行四边形,记作▱ABCD,读作“____________”, 线段BD就是▱ABCD的一条__________. 2.平行四边形的对称性 平行四边形是__________对称图形,两条对角线的交点是它 的__________. 平行 平行四边形ABCD 对角线 中心 对称中心

3.平行四边形的边和角的性质 定理平行四边形的对边 相等 定理平行四边形的对角相等 温馨提示 平行四边形的对边平行且相等,对角相等,邻角互补是它的 重要性质,为我们今后解决相关问题提供了重要的理论依据, 要熟练掌握 导航页
导航页 3.平行四边形的边和角的性质 定理 平行四边形的对边__________. 定理 平行四边形的对角__________. 温馨提示 平行四边形的对边平行且相等,对角相等,邻角互补是它的 重要性质,为我们今后解决相关问题提供了重要的理论依据, 要熟练掌握. 相等 相等
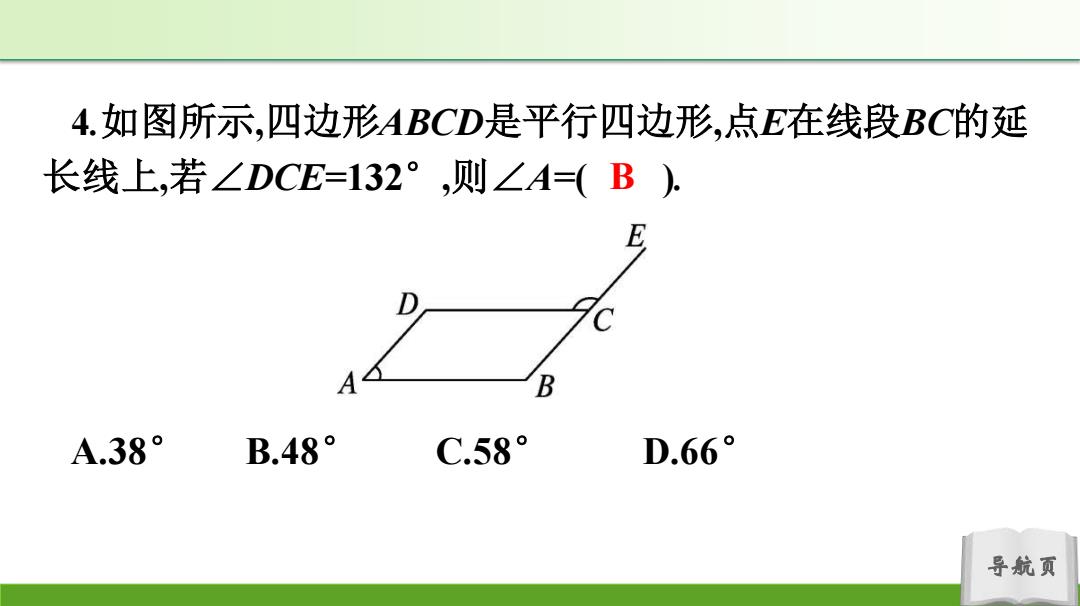
4.如图所示,四边形ABCD是平行四边形,点E在线段BC的延 长线上,若∠DCE=132°,则∠A=(B), B A.38° B.48° C.58° D.66° 导航页
导航页 4.如图所示,四边形ABCD是平行四边形,点E在线段BC的延 长线上,若∠DCE=132° ,则∠A=( ). A.38° B.48° C.58° D.66° B
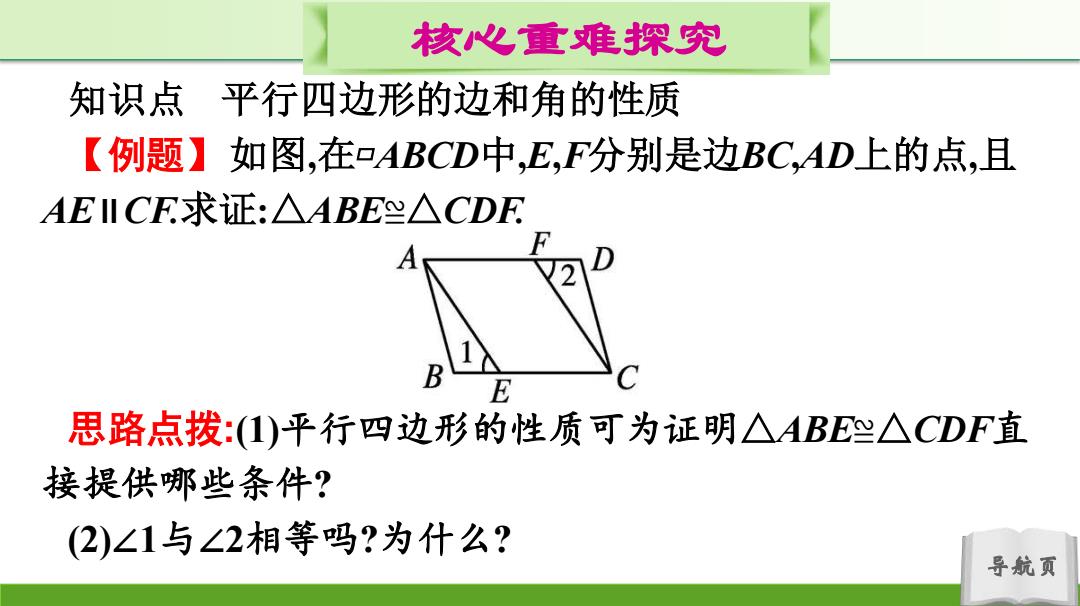
核心重难探究 知识点 平行四边形的边和角的性质 【例题】如图,在ABCD中,E,F分别是边BC,AD上的点,且 AEIICE求证:△ABE≌△CDF B E 思路点拨:(1)平行四边形的性质可为证明△ABE≌△CDF直 接提供哪些条件? (2)∠1与∠2相等吗?为什么? 导航页
导航页 核心重难探究 知识点 平行四边形的边和角的性质 【例题】如图,在▱ABCD中,E,F分别是边BC,AD上的点,且 AE∥CF.求证:△ABE≌△CDF. 思路点拨:(1)平行四边形的性质可为证明△ABE≌△CDF直 接提供哪些条件? (2)∠1与∠2相等吗?为什么?

证明:·四边形ABCD是平行四边形, .'AB=CD,∠B=∠D,ADII BC .∠2=∠FCB. .AE川CF,.∠1=∠FCB. .∠1=∠2. ..△ABE≌△CDFAAS) 导航页
导航页 证明:∵四边形ABCD是平行四边形, ∴AB=CD,∠B=∠D,AD∥BC. ∴∠2=∠FCB. ∵AE∥CF,∴∠1=∠FCB. ∴∠1=∠2. ∴△ABE≌△CDF(AAS)

【方法归纳】 1.平行四边形提供了线段的相等及平行的位置关系,也提供 了角的相等、互补关系,为证明线段的相等、角的相等、三 角形的全等提供了条件与途径 2.在解题时,能应用平行四边形直接得到的结论,就不需要再 通过三角形的全等去证明了,注意学会选择简捷的解题方法 与途径 导航页
导航页 【方法归纳】 1.平行四边形提供了线段的相等及平行的位置关系,也提供 了角的相等、互补关系,为证明线段的相等、角的相等、三 角形的全等提供了条件与途径. 2.在解题时,能应用平行四边形直接得到的结论,就不需要再 通过三角形的全等去证明了,注意学会选择简捷的解题方法 与途径

新知训练巩固 1.如图,在ABCD中,已知AC=4cm,若△ACD的周长为13cm, 则口ABCD的周长为(D) B A.26 cm B.24 cm C.20 cm D.18 cm 导航页
导航页 新知训练巩固 1.如图,在▱ABCD中,已知AC=4 cm,若△ACD的周长为13 cm, 则▱ABCD的周长为( ). A.26 cm B.24 cm C.20 cm D.18 cm D
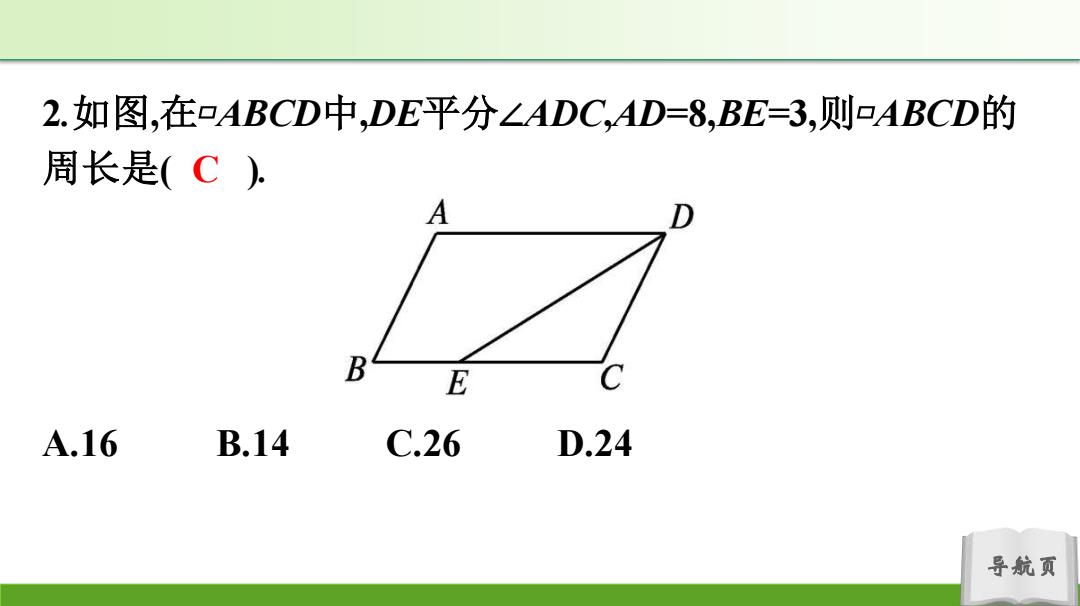
2.如图,在口ABCD中,DE平分∠ADC,AD=8,BE=3,则口ABCD的 周长是(C), A B E A.16 B.14 C.26 D.24 导航页
导航页 2.如图,在▱ABCD中,DE平分∠ADC,AD=8,BE=3,则▱ABCD的 周长是( ). A.16 B.14 C.26 D.24 C