
家庭值亚 3三角形的中位线
3 三角形的中位线

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.三角形的中位线 连接三角形两边 中点 的线段叫做三角形的中位线 2.如图,在△ABC中,点D,E,F分别是三边的中点,连接AD,EF 交于点O,则图中是△ABC的中位线的线段是(C), E A.AD B.OA C.EF D.AE B D 导航页
导航页 基础自主梳理 1.三角形的中位线 连接三角形两边__________的线段叫做三角形的中位线. 2.如图,在△ABC中,点D,E,F分别是三边的中点,连接AD,EF 交于点O,则图中是△ABC的中位线的线段是( ). A.AD B.OA C.EF D.AE 中点 C

3.三角形中位线定理 三角形的中位线平行 于第三边,且等于第三边的 一半 温馨提示 三角形有三条中位线,每一条中位线与第三边都有相应的位 置关系和数量关系.三角形的三条中位线把原三角形分成四 个全等的小三角形,因而每个小三角形的周长为原三角形周 长的一半,每个小三角形的面积为原三角形面积的四分之一 导航页
导航页 3.三角形中位线定理 三角形的中位线__________于第三边,且等于第三边的 __________. 温馨提示 三角形有三条中位线,每一条中位线与第三边都有相应的位 置关系和数量关系.三角形的三条中位线把原三角形分成四 个全等的小三角形,因而每个小三角形的周长为原三角形周 长的一半,每个小三角形的面积为原三角形面积的四分之一. 平行 一半
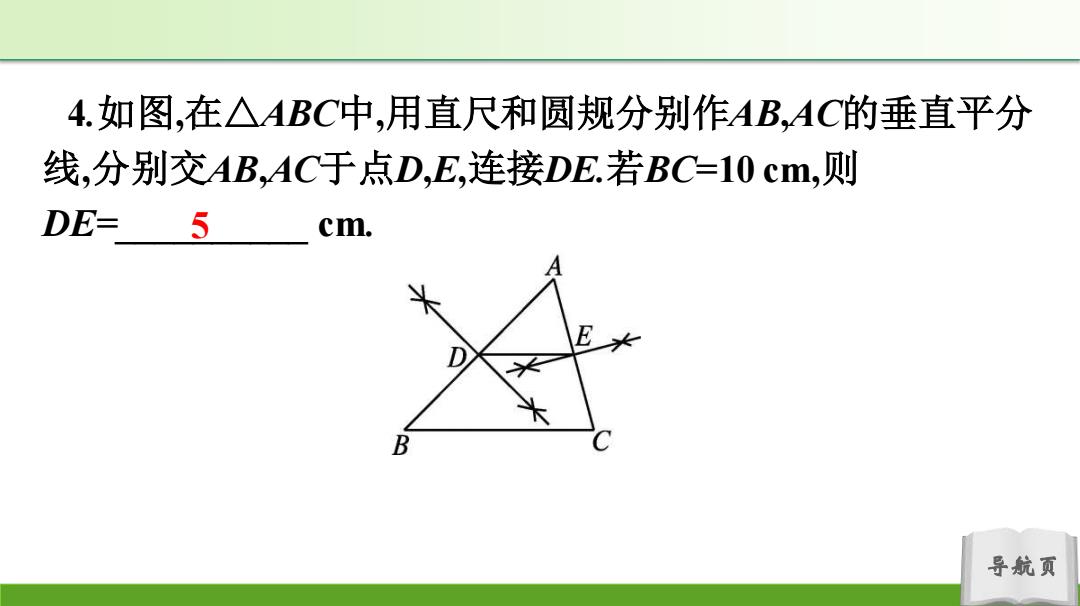
4.如图,在△ABC中,用直尺和圆规分别作AB,AC的垂直平分 线,分别交AB,AC于点D,E,连接DE.若BC=10cm,则 DE-5 cm. E D B 导航页
导航页 4.如图,在△ABC中,用直尺和圆规分别作AB,AC的垂直平分 线,分别交AB,AC于点D,E,连接DE.若BC=10 cm,则 DE=__________ 5 cm
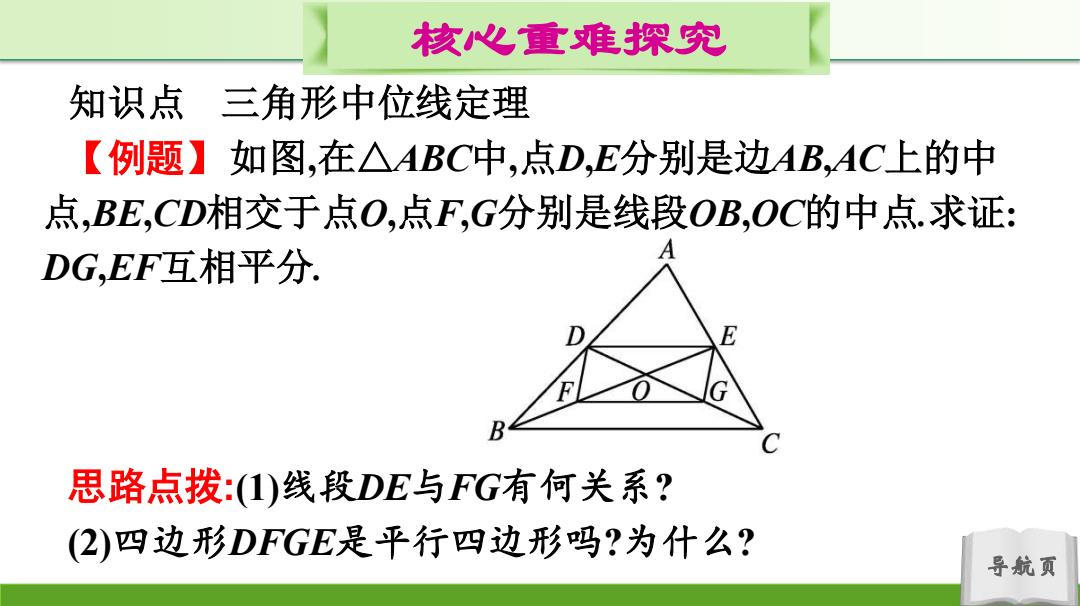
核心重难探究 知识点 三角形中位线定理 【例题】如图,在△ABC中,点D,E分别是边AB,AC上的中 点,BE,CD相交于点O,点F,G分别是线段OB,OC的中点.求证: DG,EF互相平分. B 思路点拨:1)线段DE与FG有何关系? (2)四边形DFGE是平行四边形吗?为什么? 导航页
导航页 核心重难探究 知识点 三角形中位线定理 【例题】如图,在△ABC中,点D,E分别是边AB,AC上的中 点,BE,CD相交于点O,点F,G分别是线段OB,OC的中点.求证: DG,EF互相平分. 思路点拨:(1)线段DE与FG有何关系? (2)四边形DFGE是平行四边形吗?为什么?

证明:点D,E分别是边AB,AC的中点,F,G分别是线段OB,OC 的中点, ,DE是△ABC的中位线,FG是△OBC的中位线. :DE∥BC,且DE-BC,FG∥BC,且FG-BC .DEIIFG,且DE=FG. ,:四边形DFGE是平行四边形. .DG,EF互相平分. 导航页
导航页 证明:∵点D,E分别是边AB,AC的中点,F,G分别是线段OB,OC 的中点, ∴DE是△ABC的中位线,FG是△OBC的中位线. ∴DE∥BC,且 DE=𝟏 𝟐 BC,FG∥BC,且 FG=𝟏 𝟐 BC. ∴DE∥FG,且DE=FG. ∴四边形DFGE是平行四边形. ∴DG,EF互相平分

【方法归纳】 三角形中位线定理的应用主要有: )求线段的长度; (2)证明线段相等或平行; 3)求角的度数; (4)证明线段的倍分关系 导航页
导航页 【方法归纳】 三角形中位线定理的应用主要有: (1)求线段的长度; (2)证明线段相等或平行; (3)求角的度数; (4)证明线段的倍分关系

新知训练巩固 1.不一定在三角形内部的线段是(C). A.三角形的角平分线 B.三角形的中位线 C三角形的高 D.三角形的中线 导航页
导航页 新知训练巩固 1.不一定在三角形内部的线段是( ). A.三角形的角平分线 B.三角形的中位线 C.三角形的高 D.三角形的中线 C
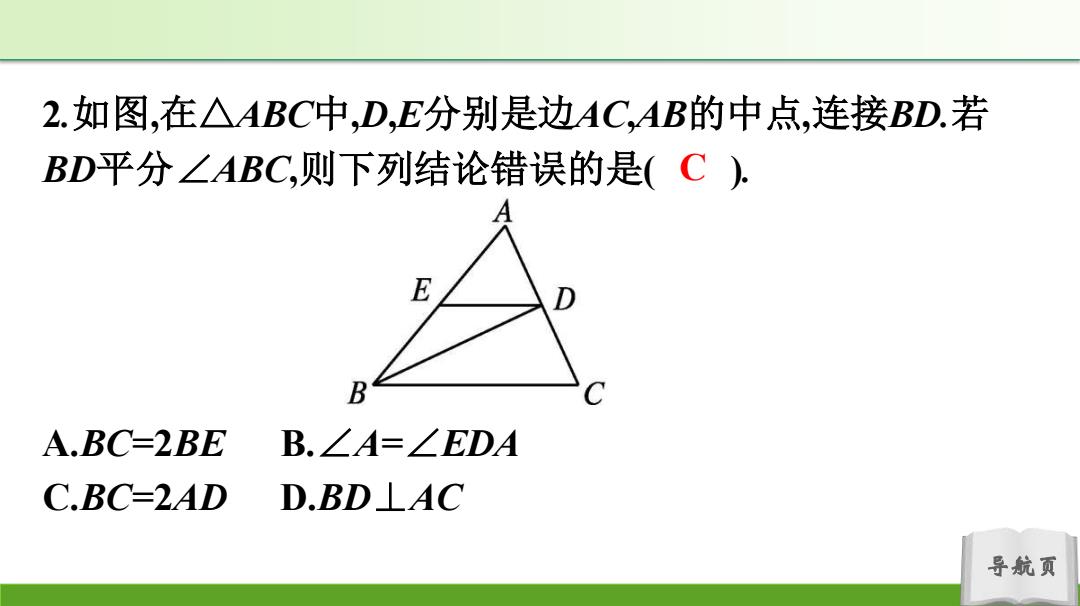
2.如图,在△ABC中,D,E分别是边AC,AB的中点,连接BD.若 BD平分∠ABC,则下列结论错误的是(C),. E B A.BC-2BE B.∠A=∠EDA C.BC-2AD D.BD⊥AC 导航页
导航页 2.如图,在△ABC中,D,E分别是边AC,AB的中点,连接BD.若 BD平分∠ABC,则下列结论错误的是( ). A.BC=2BE B.∠A=∠EDA C.BC=2AD D.BD⊥AC C