
家庭馆四 微专题 一元一次不等式(组)的解法及应用
微专题一 一元一次不等式(组)的解法及应用

1.已知关于x的不等式2m,m 1 1. (1)当=1时,求该不等式的解集; (2)当m取何值时,该不等式有解?并求出解集 解:(1)当m=1时,22>2-1,解得2 (2)由2mm>2l,得m+10rc2(m1 当-1时,原不等式有解; 当心-1时,原不等式的解集为x2
1.已知关于 x 的不等式𝟐𝒎-𝒎𝒙 𝟐 > 𝟏 𝟐 x-1. (1)当m=1时,求该不等式的解集; (2)当m取何值时,该不等式有解?并求出解集. 解:(1)当 m=1 时, 𝟐-𝒙 𝟐 > 𝟏 𝟐 x-1,解得 x 𝟏 𝟐 x-1, 当m≠-1时,原不等式有解; 当m>-1时,原不等式的解集为x2. 得(m+1)x<2(m+1)

4x>2x-8, 2.解不等式组 s. X-1 解:解不等式4x>2x-8,得x>-4. 解不等式号≤告,得3. 所以原不等式组的解集为-4<x≤3
2.解不等式组 𝟒𝒙 > 𝟐𝒙-𝟖, 𝒙-𝟏 𝟑 ≤ 𝒙+𝟏 𝟔 . 解:解不等式4x>2x-8,得x>-4. 解不等式𝒙-𝟏 𝟑 ≤ 𝒙+𝟏 𝟔 ,得 x≤3. 所以原不等式组的解集为-4<x≤3

3.某快递公司为了提高工作效率,计划购买A,B两种型号的机 器人来搬运货物,己知每台A型机器人比每台B型机器人每天 多搬运20吨,并且3台A型机器人和2台B型机器人每天共搬运 货物460吨. (1)求每台A型机器人和每台B型机器人每天分别搬运货物多 少吨? (2)每台A型机器人售价3万元,每台B型机器人售价2万元,该公 司计划采购A,B两种型号的机器人共20台,必须满足每天搬运 的货物不低于1800吨,请根据以上要求,求出A,B两种机器人 分别采购多少台时,所需费用最低?最低费用是多少?
3.某快递公司为了提高工作效率,计划购买A,B两种型号的机 器人来搬运货物,已知每台A型机器人比每台B型机器人每天 多搬运20吨,并且3台A型机器人和2台B型机器人每天共搬运 货物460吨. (1)求每台A型机器人和每台B型机器人每天分别搬运货物多 少吨? (2)每台A型机器人售价3万元,每台B型机器人售价2万元,该公 司计划采购A,B两种型号的机器人共20台,必须满足每天搬运 的货物不低于1 800吨,请根据以上要求,求出A,B两种机器人 分别采购多少台时,所需费用最低?最低费用是多少?

解:1)设每台A型机器人每天搬运货物x吨,每台B型机器人每 天搬运货贷物y吨, 则xy=20, (3x+2y=460, 解得 x=100, y=80. 故每台A型机器人每天搬运货物100吨,每台B型机器人每天 搬运货物80吨
解:(1)设每台A型机器人每天搬运货物x吨,每台B型机器人每 天搬运货物y吨, 则 𝒙-𝒚 = 𝟐𝟎, 𝟑𝒙 + 𝟐𝒚 = 𝟒𝟔𝟎, 解得 𝒙 = 𝟏𝟎𝟎, 𝒚 = 𝟖𝟎. 故每台A型机器人每天搬运货物100吨,每台B型机器人每天 搬运货物80吨

(2)设采购A型机器人m台,采购B型机器人(20-m台,总费用为 以 由100m+80(20-m)≥1800, 解得m2l0. w=3m+2(20-1m)=m+40. ·w随着m的减少而减少, :当=10时,w有最小值,w最小=10+40=50. ,·A,B两种机器人均采购10台时,所需费用最低,最低费用是 50万元
(2)设采购A型机器人m台,采购B型机器人(20-m)台,总费用为 w. 由100m+80(20-m)≥1 800, 解得m≥10. w=3m+2(20-m)=m+40. ∵w随着m的减少而减少, ∴当m=10时,w有最小值,w最小=10+40=50. ∴A,B两种机器人均采购10台时,所需费用最低,最低费用是 50万元
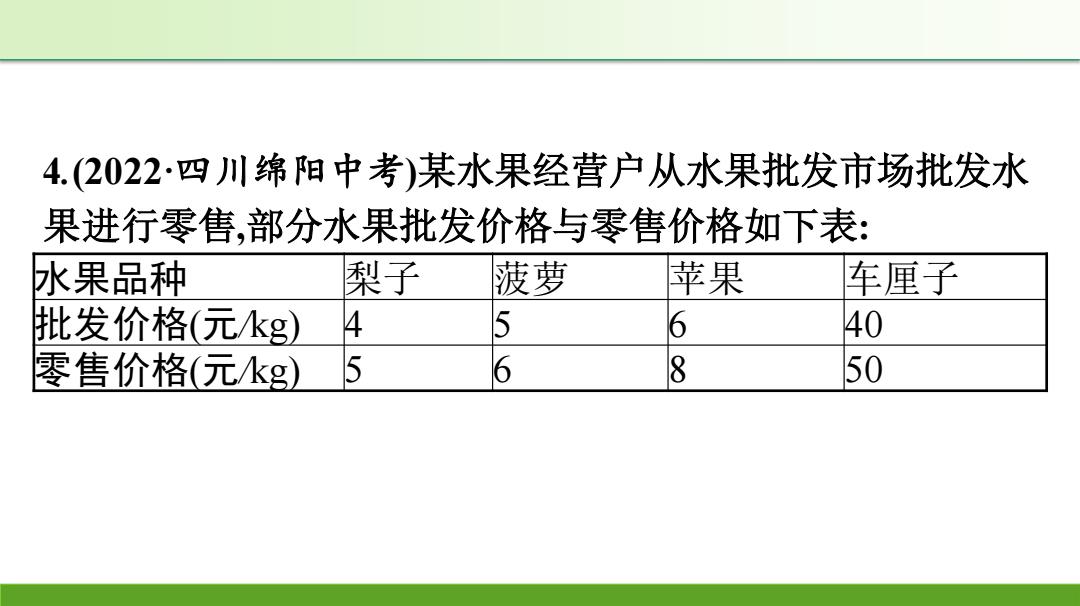
4.(2022·四川绵阳中考)某水果经营户从水果批发市场批发水 果进行零售,部分水果批发价格与零售价格如下表: 水果品种 梨子 菠萝 苹果 车厘子 批发价格(元kg) 4 5 6 40 零售价格(元kg) 5 6 8 50
4.(2022·四川绵阳中考)某水果经营户从水果批发市场批发水 果进行零售,部分水果批发价格与零售价格如下表: 水果品种 梨子 菠萝 苹果 车厘子 批发价格(元/kg) 4 5 6 40 零售价格(元/kg) 5 6 8 50

请解答下列问题: (1)第一天,该经营户用1700元批发了菠萝和苹果共300kg,当 日全部售出,求这两种水果获得的总利润. (2)第二天,该经营户依然用1700元批发了菠萝和苹果,当日销 售结束清点盘存时发现进货单丢失,只记得这两种水果的批 发量均为正整数且菠萝的进货量不低于88kg,这两种水果已 全部售出且总利润高于第一天这两种水果的总利润,清通过 计算说明该经营户第二天批发这两种水果可能的方案有哪些
请解答下列问题: (1)第一天,该经营户用1 700元批发了菠萝和苹果共300 kg,当 日全部售出,求这两种水果获得的总利润. (2)第二天,该经营户依然用1 700元批发了菠萝和苹果,当日销 售结束清点盘存时发现进货单丢失,只记得这两种水果的批 发量均为正整数且菠萝的进货量不低于88 kg,这两种水果已 全部售出且总利润高于第一天这两种水果的总利润,请通过 计算说明该经营户第二天批发这两种水果可能的方案有哪些

解:()设第一天该经营户批发了菠萝xkg,苹果ykg x+y=300, 根据题意得5x+6y=1700, (x=100, 解得=200. (6-5)x+(8-6)y=(6-5)X100+(8-6)X200=500(元). 故这两种水果获得的总利润为500元
解:(1)设第一天该经营户批发了菠萝x kg,苹果y kg. 根据题意得 𝒙 + 𝒚 = 𝟑𝟎𝟎, 𝟓𝒙 + 𝟔𝒚 = 𝟏 𝟕𝟎𝟎, 解得 𝒙 = 𝟏𝟎𝟎, 𝒚 = 𝟐𝟎𝟎. (6-5)x+(8-6)y=(6-5)×100+(8-6)×200=500(元). 故这两种水果获得的总利润为500元

(2)设第二天该经营户购进mkg菠萝,则购进1700-5m 6 kg苹果 m≥88, 根据题意得 6-5m+8-6)×17085m>500, 解得88≤m<100. 叉m17005m均为正整数. 6 .m的值为88,94, ,:该经营户第二天共有2种批发水果的方案, 方案1:购进88kg菠萝,210kg苹果; 方案2:购进94kg菠萝,205kg苹果
(2)设第二天该经营户购进 m kg 菠萝,则购进𝟏 𝟕𝟎𝟎-𝟓𝒎 𝟔 kg 苹果. 根据题意得 𝒎 ≥ 𝟖𝟖, (𝟔-𝟓)𝒎 + (𝟖-𝟔) × 𝟏 𝟕𝟎𝟎-𝟓𝒎 𝟔 > 𝟓𝟎𝟎, 解得 88≤m<100. 又 m, 𝟏 𝟕𝟎𝟎-𝟓𝒎 𝟔 均为正整数. ∴m的值为88,94, ∴该经营户第二天共有2种批发水果的方案, 方案1:购进88 kg菠萝,210 kg苹果; 方案2:购进94 kg菠萝,205 kg苹果