
家庭们亚 1不等关系
1 不等关系

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.不等式 一般地,用符号“”(或“≥”)连接的式 子叫做不等式 2.列不等式表示不等关系的步骤 (1)审题,分清数量的大小关系; (2)列出相等的代数式,用表示不等式关系的符号列出不等 式 导航页
导航页 基础自主梳理 1.不等式 一般地,用符号“”(或“______”)连接的式 子叫做不等式. 2.列不等式表示不等关系的步骤 (1)审题,分清数量的大小关系; (2)列出相等的代数式,用表示不等式关系的符号列出不等 式. ≤ ≥
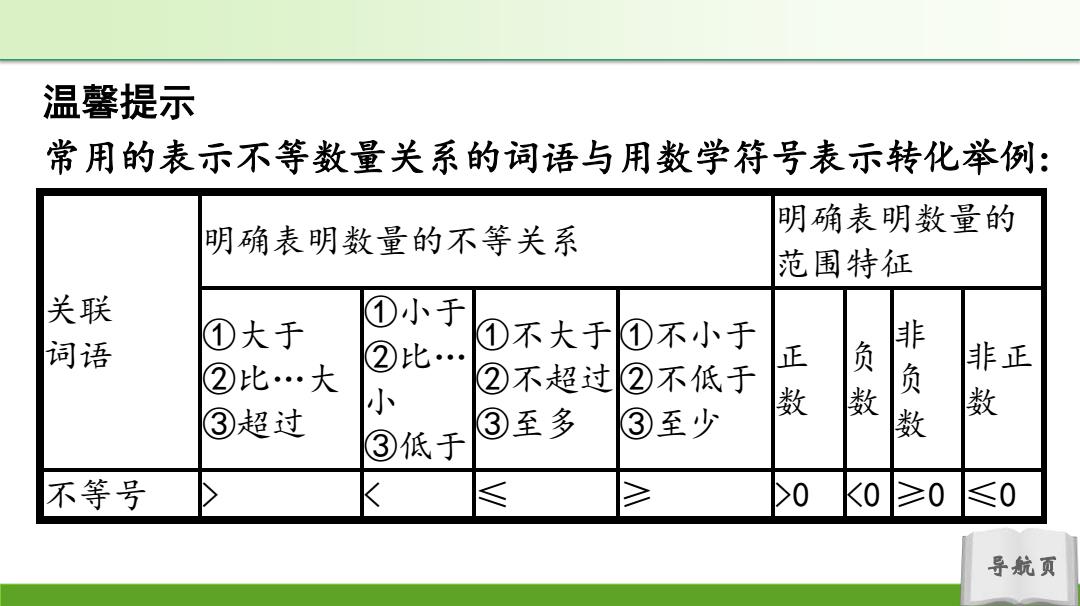
温馨提示 常用的表示不等数量关系的词语与用数学符号表示转化举例: 明确表明数量的 明确表明数量的不等关系 范围特征 关联 ①小于 词语 ①大于 ②比… ①不大于 ①不小于 ②比…大 ②不超过 ②不低于 正 负数 非负 非正 小 ③至多 ③至少 数 ③超过 ③低于 不等号 ≤ 0 ≥0 ≤0 导航页
导航页 温馨提示 常用的表示不等数量关系的词语与用数学符号表示转化举例: 关联 词语 明确表明数量的不等关系 明确表明数量的 范围特征 ①大于 ②比…大 ③超过 ①小于 ②比… 小 ③低于 ①不大于 ②不超过 ③至多 ①不小于 ②不低于 ③至少 正 数 负 数 非 负 数 非正 数 不等号 > 0 <0 ≥0 ≤0

3.根据下列不等关系列不等式 (山)x与y的和不大于3; x+y≤3 (2)a与b的差不小于a与b的和, -b≥a+b 导航页
导航页 3.根据下列不等关系列不等式. (1)x与y的和不大于 ; (2)a与b的差不小于a与b的和. 𝟏 𝟑 x+y≤ 𝟏 𝟑 a-b≥a+b

核心重难探究 知识点一不等式的定义 【例1】判断下列各式哪些是等式,哪些是不等式. (1)40;3)x<2x-5; (4)x=2x+3;(⑤)32+;(6)2+2a≥4a-2. 思路点拨:根据等式与不等式的定义逐一识别即可 导航页
导航页 核心重难探究 知识点一 不等式的定义 【例1】判断下列各式哪些是等式,哪些是不等式. (1)40;(3)x<2x-5; (4)x=2x+3;(5)3a 2+a;(6)a 2+2a≥4a-2. 思路点拨:根据等式与不等式的定义逐一识别即可

解:1)40是不等式. (3)x<2x-5是不等式. (4)x=2x+3是等式. (5)3a2+是代数式 (6)2+2M≥4a-2是不等式 故(1)2)3)6)是不等式,(4)是等式 导航页
导航页 解 :(1)4 0是不等式 . (3)x< 2 x - 5是不等式 . (4)x= 2x+ 3是等式 . (5)3 a 2+a是代数式. (6) a 2 + 2 a ≥ 4 a - 2是不等式. 故(1)(2)(3)(6)是不等式,(4)是等式

【方法归纳】 识别不等式的关键是把握不等式的定义,掌握不等号的符号 表示注意用符号“”连接的式子也是不等式 导航页
导航页 【方法归纳】 识别不等式的关键是把握不等式的定义,掌握不等号的符号 表示.注意用符号“≠”连接的式子也是不等式

知识点二列不等式 【例2】用适当的符号表示下列关系: (1)x的3与x的2倍的和是非负数;+2x≥0 (2)c与4的和的30%不大于-2;30%(c+4)≤-2 3)x除以2的商加上2,至多为5;2+2≤5 (4)a与b两数和的平方不可能大于3;(a+b)2≤3 (⑤)爸爸的年龄x比儿子的年龄y的2倍还大x>2y 思路点拨:列不等式时,要抓住“关键词”的意义 如(1)“非负数”;(2)“不大于”;3)“至多”;(4)“不可能大于”; 5⑤)“2倍还大”等: 导航页
导航页 知识点二 列不等式 【例2】用适当的符号表示下列关系: (1)x的 与x的2倍的和是非负数; (2)c与4的和的30%不大于-2; (3)x除以2的商加上2,至多为5; (4)a与b两数和的平方不可能大于3; (5)爸爸的年龄x比儿子的年龄y的2倍还大. 𝟏 𝟑 思路点拨:列不等式时,要抓住“关键词”的意义. 如(1)“非负数”;(2)“不大于”;(3)“至多”;(4)“不可能大于”; (5)“2倍还大”等. 𝒙 𝟑 +2x≥0 30%(c+4)≤-2 𝒙 𝟐 +2≤5 (a+b) 2≤3 x>2y

【方法归纳】 列不等式的重点与难点是抓住关键词,弄清不等关系.如“正 数”“非负数”“非正数”“至多”“至少”“不大于”“不小于”等这 样的表述在解题时,一定要使用正确的不等式符号表示其实 际意义, 导航页
导航页 【方法归纳】 列不等式的重点与难点是抓住关键词,弄清不等关系.如“正 数”“非负数”“非正数”“至多”“至少”“不大于”“不小于”等这 样的表述.在解题时,一定要使用正确的不等式符号表示其实 际意义