
家庭你亚 第2课时 三角形的三条角平分线
第2课时 三角形的三条角平分线

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.三角形的三条角平分线 三角形的三条角平分线相交于一点,并且这一点到三 条边的距离相等 温馨提示 任意三角形的三条角平分线的交点均在三角形的内部. 导航页
导航页 基础自主梳理 1.三角形的三条角平分线 三角形的三条角平分线相交于__________,并且这一点到三 条边的距离__________. 温馨提示 任意三角形的三条角平分线的交点均在三角形的内部. 一点 相等

2.判断下面结论的对错 ()在三角形内部,到三角形三边距离相等的点只有一个 (√) (2)在同一平面内,到三角形三边所在直线距离相等的点只 有一个.(×) (3)三角形的三条角平分线交于一点(√) (4)等腰三角形的底边中点到两腰的距离相等(√) (⑤)三角形是以它的角平分线为对称轴的轴对称图形(×) 导航页
导航页 2.判断下面结论的对错. (1)在三角形内部,到三角形三边距离相等的点只有一个. ( ) (2)在同一平面内,到三角形三边所在直线距离相等的点只 有一个.( ) (3)三角形的三条角平分线交于一点.( ) (4)等腰三角形的底边中点到两腰的距离相等.( ) (5)三角形是以它的角平分线为对称轴的轴对称图形.( ) √ × √ √ ×
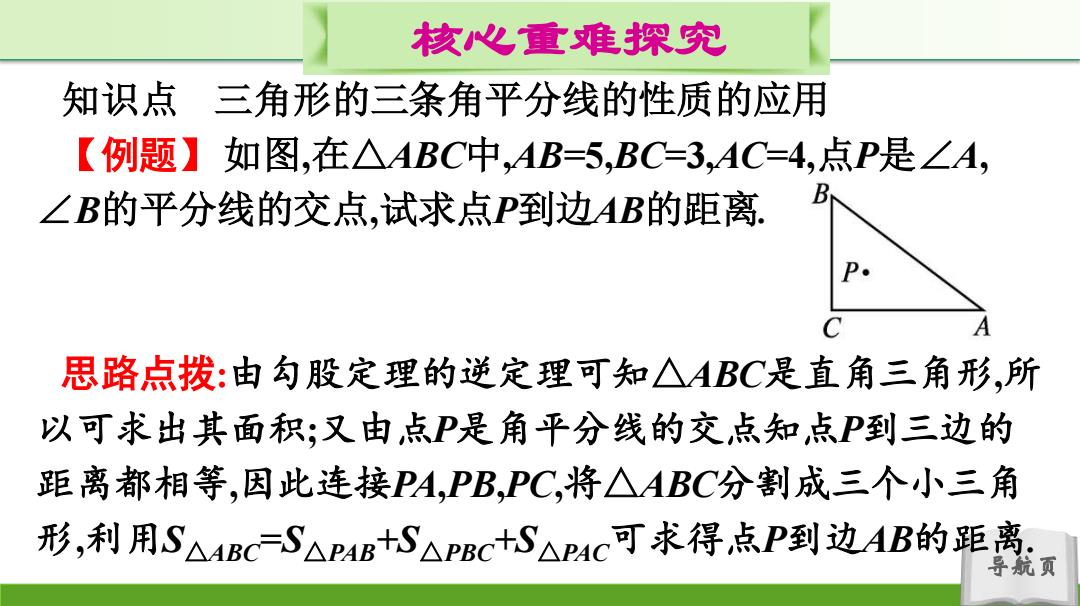
核心重难探究 知识点 三角形的三条角平分线的性质的应用 【例题】如图,在△ABC中,AB=5,BC=3,AC=4,点P是∠A, ∠B的平分线的交点,试求点P到边AB的距离: B P。 思路点拨:由勾股定理的逆定理可知△ABC是直角三角形,所 以可求出其面积;又由点P是角平分线的交点知点P到三边的 距离都相等,因此连接PA,PB,PC,将△ABC分割成三个小三角 形,利用S△4BCS△PAB+S△PBC+S△P4C可求得点P到边AB的距离 航页
导航页 核心重难探究 知识点 三角形的三条角平分线的性质的应用 【例题】 如图,在△ABC中,AB=5,BC=3,AC=4,点P是∠A, ∠B的平分线的交点,试求点P到边AB的距离. 思路点拨:由勾股定理的逆定理可知△ABC是直角三角形,所 以可求出其面积;又由点P是角平分线的交点知点P到三边的 距离都相等,因此连接PA,PB,PC,将△ABC分割成三个小三角 形,利用S△ABC=S△PAB+S△PBC+S△PAC可求得点P到边AB的距离

解:如图,连接PA,PB,PC :点P是∠A,∠B的平分线的交点, B ,·点P到△ABC三边的距离相等 设点P到△ABC三边的距离为h, 则S△MBC=S△PAB+S△PAC+S△PBC -AB-h+ACh+BC:h-h(AB+AC+BC). 又·32+42=52,即BC2+AC2=AB2, .·△ABC为直角三角形. 导航页
导航页 解:如图,连接PA,PB,PC. ∵点P是∠A,∠B的平分线的交点, ∴点P到△ABC三边的距离相等. 设点P到△ABC三边的距离为h, 则S△ABC=S△PAB+S△PAC+S△PBC = 𝟏 𝟐 AB·h+𝟏 𝟐 AC·h+𝟏 𝟐 BC·h=𝟏 𝟐 h(AB+AC+BC). 又∵3 2+4 2=5 2 ,即BC2+AC2=AB2 , ∴△ABC为直角三角形

(AB+AC+BC)-AC-BC, 即×(5+4+3)h3×4×3. ,h=l,即,点P到边AB的距离为1. 【方法归纳】 三角形角平分线的交点与三角形三个顶点的连线把原三角 形分割成三个小三角形,利用分割成的三个小三角形的面积 的和等于原三角形的面积,进而求出角平分线的交点到三边 的距离这是面积法解题的有效途径 导航页
导航页 ∴ 𝟏 𝟐 h(AB+AC+BC)= 𝟏 𝟐 AC·BC, 即 𝟏 𝟐 ×(5+4+3)·h=𝟏 𝟐 ×4×3. ∴h=1,即点 P 到边 AB 的距离为 1. 【方法归纳】 三角形角平分线的交点与三角形三个顶点的连线把原三角 形分割成三个小三角形,利用分割成的三个小三角形的面积 的和等于原三角形的面积,进而求出角平分线的交点到三边 的距离.这是面积法解题的有效途径

新知训练巩固 1.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧, 交x轴于点M,交轴于点N,再分别以点M,N为圆心,大于MN 的长为半径画弧,两弧在第二象限交于点P若点P的坐标为 (a,b),则a与b的数量关系为+b=0 导航页
导航页 新知训练巩固 1.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧, 交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于 的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为 (a,b),则a与b的数量关系为__________. 𝟏 𝟐 MN a+b=0
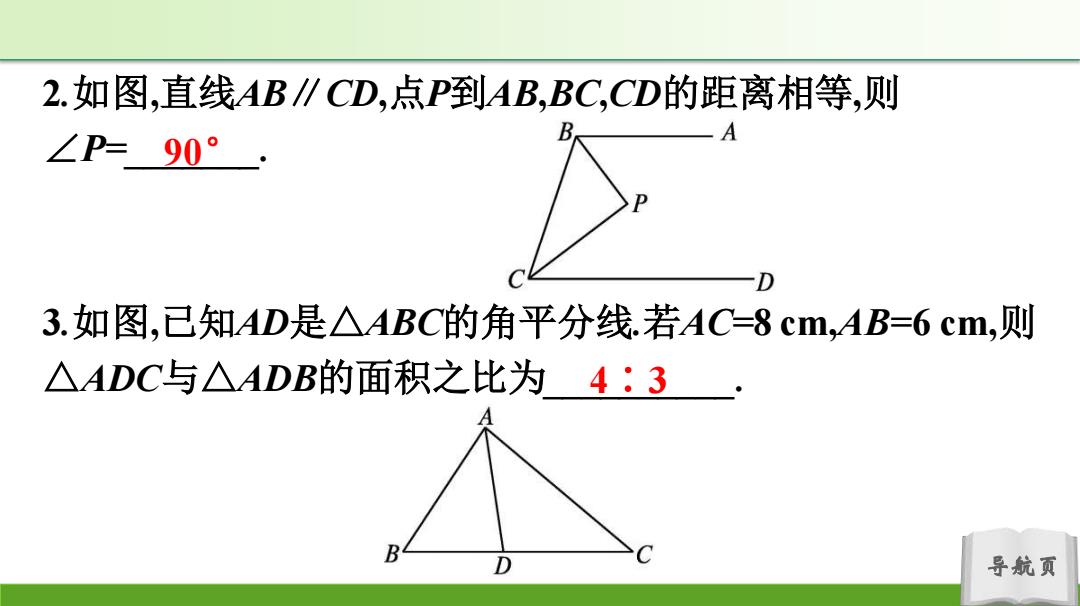
2.如图,直线AB∥CD,点P到AB,BC,CD的距离相等,则 ∠P=90° B A D 3.如图,已知AD是△ABC的角平分线.若AC=8cm,AB=6cm,则 △ADC与△ADB的面积之比为4:3 B D C 导航页
导航页 2.如图,直线AB∥CD,点P到AB,BC,CD的距离相等,则 ∠P=_______. 3.如图,已知AD是△ABC的角平分线.若AC=8 cm,AB=6 cm,则 △ADC与△ADB的面积之比为__________. 90° 4∶3

路漫漫其修远兮 吾将上下而求索
路漫漫其修远兮 吾将上下而求索