
家庭值业 第1课时 角平分线的定理
第1课时 角平分线的定理

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.角平分线的性质定理 角平分线上的点到这个角的两边的距离 相等 温馨提示 应用角平分线的性质要具有两个条件: ()点在角的平分线上; (2)过这一点作角的两边的垂线段 角平分线的性质是证明两线段相等的重要方法之一,而且不 用再证明两个三角形全等. 导航页
导航页 基础自主梳理 1.角平分线的性质定理 角平分线上的点到这个角的两边的距离__________. 温馨提示 应用角平分线的性质要具有两个条件: (1)点在角的平分线上; (2)过这一点作角的两边的垂线段. 角平分线的性质是证明两线段相等的重要方法之一,而且不 用再证明两个三角形全等. 相等
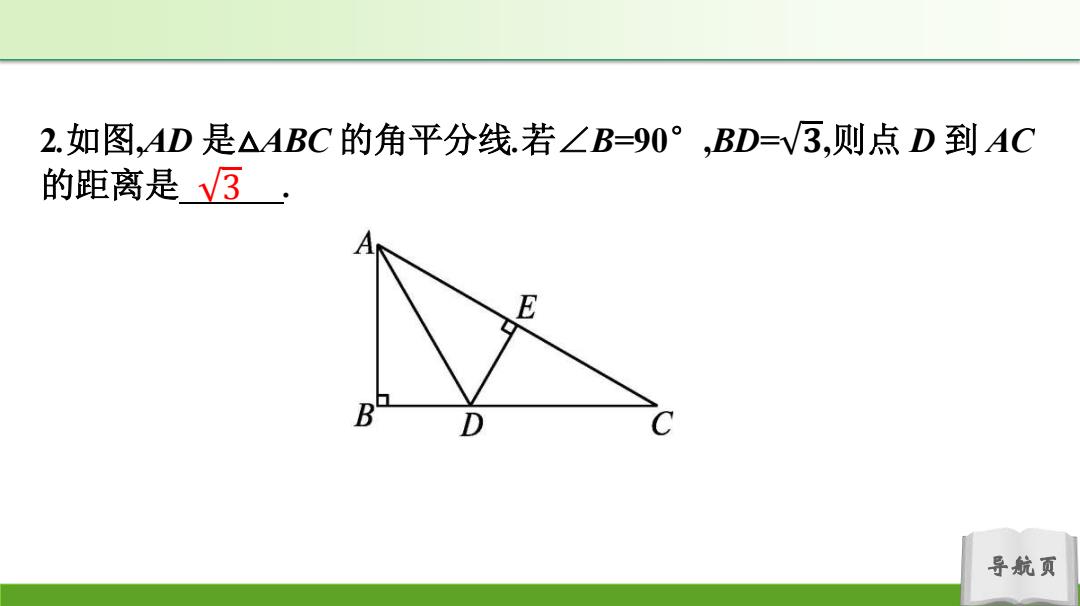
2.如图,AD是△ABC的角平分线若∠B=90°,BD=V3,则点D到AC 的距离是√ E 导航页
导航页 2.如图,AD 是△ABC 的角平分线.若∠B=90° ,BD= 𝟑,则点 D 到 AC 的距离是 3
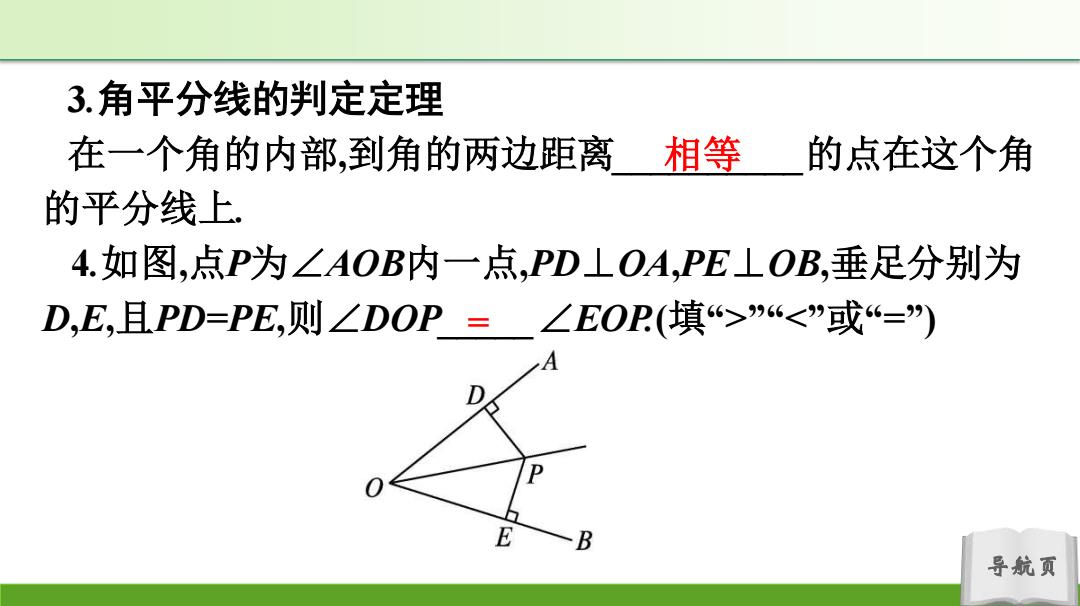
3.角平分线的判定定理 在一个角的内部,到角的两边距离 相等 的点在这个角 的平分线上 4.如图,点P为∠AOB内一点,PD⊥OA,PE⊥OB,垂足分别为 D,E,且PD=PE,则∠DOP=∠EOP(填>”“<”或“=) E B 导航页
导航页 3.角平分线的判定定理 在一个角的内部,到角的两边距离__________的点在这个角 的平分线上. 4.如图,点P为∠AOB内一点,PD⊥OA,PE⊥OB,垂足分别为 D,E,且PD=PE,则∠DOP_____∠EOP.(填“>”“<”或“=”) 相等 =

核心重难探究 知识点 角平分线的判定 【例题】如图,点B,C分别在∠MAN的两边上,BD⊥AM于点 D,CE⊥AN于点E,BD,CE相交于点F,且BF=CF M 求证:点F在∠MAN的平分线上 EB N 思路点拨:(1)欲证,点F在∠MAN的平分线上,只需证哪两条线 段相等? (2)图中哪两个三角形全等?为什么? 导航页
导航页 核心重难探究 知识点 角平分线的判定 【例题】如图,点B,C分别在∠MAN的两边上,BD⊥AM于点 D,CE⊥AN于点E,BD,CE相交于点F,且BF=CF. 求证:点F在∠MAN的平分线上. 思路点拨:(1)欲证点F在∠MAN的平分线上,只需证哪两条线 段相等? (2)图中哪两个三角形全等?为什么?

证明:·BD⊥AM,CE⊥AN, .·∠CDF=∠BEF=90°. (∠CDF=∠BEF, 在△DCF和△EBF中,}LDFC=∠BFE, BF=CF, .·△DCF≌△EBF(AAS) ..FD-FE. .·点F在∠MAN的平分线上. 导航页
导航页 证明:∵BD⊥AM,CE⊥AN, ∴∠CDF=∠BEF=90° . 在△DCF 和△EBF 中, ∠𝑪𝑫𝑭 = ∠𝑩𝑬𝑭, ∠𝑫𝑭𝑪 = ∠𝑩𝑭𝑬, 𝑩𝑭 = 𝑪𝑭, ∴△DCF≌△EBF(AAS). ∴FD=FE. ∴点F在∠MAN的平分线上

【方法归纳】 1.判定角平分线时,需要满足两个条件:“垂直”和“相等”. 2.我们在进行证明的分析过程中,往往采用“执果索因”的方 式,即由要证明的结论逆推到已知条件,而证明的书写则一般 是“执因索果”的顺序,这一点应注意把握好.当然,对于较复杂 的证明题,分析时往往采用“两头凑”的方式,即结合结论与已 知条件进行全盘考虑 导航页
导航页 【方法归纳】 1.判定角平分线时,需要满足两个条件:“垂直”和“相等” . 2.我们在进行证明的分析过程中,往往采用“执果索因”的方 式,即由要证明的结论逆推到已知条件,而证明的书写则一般 是“执因索果”的顺序,这一点应注意把握好.当然,对于较复杂 的证明题,分析时往往采用“两头凑”的方式,即结合结论与已 知条件进行全盘考虑

新知训练巩固 1.如图,在CD上找一点P,使得它到OA,OB的距离相等,则应找 到(B) A.线段CD的中点 B.CD与∠AOB平分线的交点 C.OC的垂直平分线与CD的交点 B D.OD的垂直平分线与CD的交点 导航页
导航页 新知训练巩固 1.如图,在CD上找一点P,使得它到OA,OB的距离相等,则应找 到( ). A.线段CD的中点 B.CD与∠AOB平分线的交点 C.OC的垂直平分线与CD的交点 D.OD的垂直平分线与CD的交点 B

2.如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点 D,DE⊥AB,垂足为E.若DE=1,则BC的长为( ).A E B C D A.2h2 B.v2+√3 C.2+3 D.3 导航页
导航页 2.如图,在△ABC中,∠B=30° ,∠C=45° ,AD平分∠BAC交BC于点 D,DE⊥AB,垂足为E.若DE=1,则BC的长为( ). A.2+ 𝟐 B. 𝟐 + 𝟑 C.2+ 𝟑 D.3 A