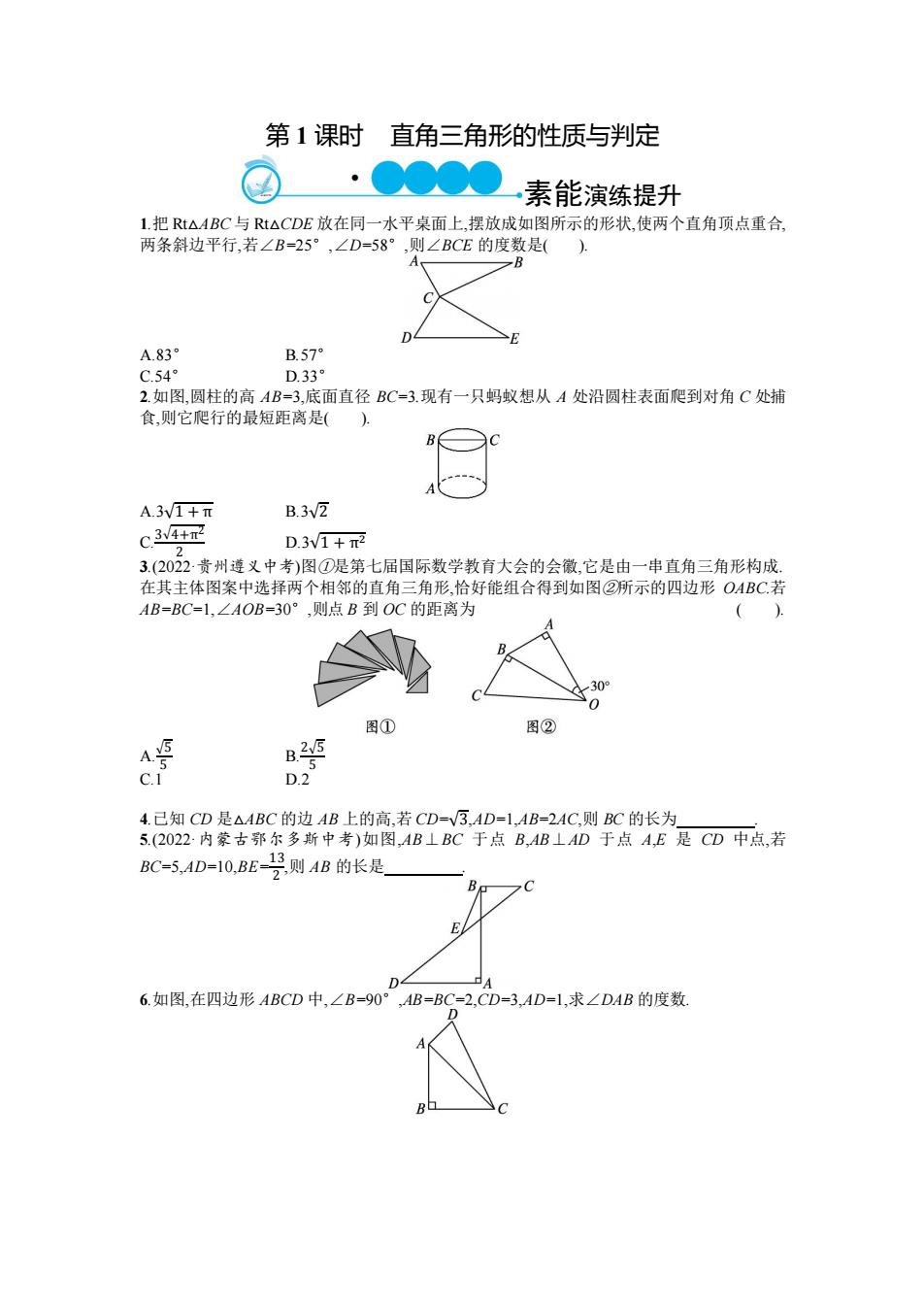
第1课时 直角三角形的性质与判定 人▲人一素能演练提升 1把Rt△ABC与Rt△CDE放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合, 两条斜边平行,若∠B=25°,∠D=58°,则∠BCE的度数是(). -B A.83 B.57 C.54 D.33 2.如图,圆柱的高AB=3,底面直径BC=3.现有一只蚂蚁想从A处沿圆柱表面爬到对角C处捕 食,则它爬行的最短距离是( A.3V1+元 B.3v2 C.3V4+R D.3V1+π2 3.(2022贵州遵义中考)图①是第七届国际数学教育大会的会徽,它是由一串直角三角形构成. 在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC若 AB=BC=1,∠AOB=30°,则点B到OC的距离为 () 30 图① 图② A号 B25 c D.2 4.己知CD是△ABC的边AB上的高,若CD=V3,AD=1,AB=2AC,则BC的长为 5.(2022内蒙古鄂尔多斯中考)如图,AB⊥BC于点B,AB⊥AD于点A,E是CD中点,若 BC=5,AD=10,BE-号则AB的长是 C 6.如图,在四边形ABCD中,∠B-=90°,AB=BC=2,CD=3,AD=1,求∠DAB的度数 D
第 1 课时 直角三角形的性质与判定 素能演练提升 1.把 Rt△ABC 与 Rt△CDE 放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合, 两条斜边平行,若∠B=25°,∠D=58°,则∠BCE 的度数是( ). A.83° B.57° C.54° D.33° 2.如图,圆柱的高 AB=3,底面直径 BC=3.现有一只蚂蚁想从 A 处沿圆柱表面爬到对角 C 处捕 食,则它爬行的最短距离是( ). A.3√1 + π B.3√2 C. 3√4+π 2 2 D.3√1 + π2 3.(2022·贵州遵义中考)图①是第七届国际数学教育大会的会徽,它是由一串直角三角形构成. 在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形 OABC.若 AB=BC=1,∠AOB=30°,则点 B 到 OC 的距离为 ( ). A. √5 5 B. 2√5 5 C.1 D.2 4.已知 CD 是△ABC 的边 AB 上的高,若 CD=√3,AD=1,AB=2AC,则 BC 的长为 . 5.(2022·内蒙古鄂尔多斯中考)如图,AB⊥BC 于点 B,AB⊥AD 于点 A,E 是 CD 中点,若 BC=5,AD=10,BE=13 2 ,则 AB 的长是 . 6.如图,在四边形 ABCD 中,∠B=90°,AB=BC=2,CD=3,AD=1,求∠DAB 的度数

【素能演练提升】 1.B2.C3.B4.23或2V75.12 6.解:‘∠B-90°,AB=BC-2, :AC2=AB2+BC2=8,∠BAC=45° 又:CD=3.DA=1. .:AC2+DA2-8+1-9 又:CD2=9 .AC2+DA2=CD2 ,:△ACD是直角三角形 .:∠CAD=90°. :∠DAB=45°+90°=135°. 故∠DAB的度数为135°
【素能·演练提升】 1.B 2.C 3.B 4.2√3或 2√7 5.12 6.解 ∵∠B=90°,AB=BC=2, ∴AC2=AB2+BC2=8,∠BAC=45°. 又∵CD=3,DA=1, ∴AC2+DA2=8+1=9. 又∵CD2=9, ∴AC2+DA2=CD2 . ∴△ACD 是直角三角形. ∴∠CAD=90°. ∴∠DAB=45°+90°=135°. 故∠DAB 的度数为 135°