第1课时旋转的概念与性质 素能演练提升 1.将长方形ABCD旋转到长方形A'B'CD的位置,且A与A',B与B',C与C,D与D分别为对 应点,则下列结论不一定成立的是() A.AB=A'B' B.AB∥A'B C.∠A=∠A' D.△ABC≌△A'B'C 2.如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度得到△MMP1,则其旋转中心是 () N A.点D B.点C C.点B D.点A 3如图,在△40B中,A0-1,B0-AB-号将△4OB绕点0按逆时针方向旋转90°,得到△4OB连 接AA',则线段AA的长为() A.1 B.V2 c D.V2 4.如图,在Rt△ABC中,∠BAC-90°,AB=2.将△ABC绕点A按顺时针方向旋转至△AB1C的位 置,连接CC1,点B1恰好落在边BC的中点处,则CC的长为 B 5.如图,将△OAB绕点O逆时针旋转两次得到△OA"B”,每次旋转的角度都是50°.若∠ B"OA=120°.则∠AOB= 6.如图,将正方形CFED旋转后能与正方形ABCD重合,则图形所在的平面上可以作为旋转中 心的点共有」 个 D 7.如图,把一块瓷砖ABCD直立于地面上,然后将其轻轻推倒.在这个过程中,点A保持不动,四 边形ABCD旋转到AB'CD的位置
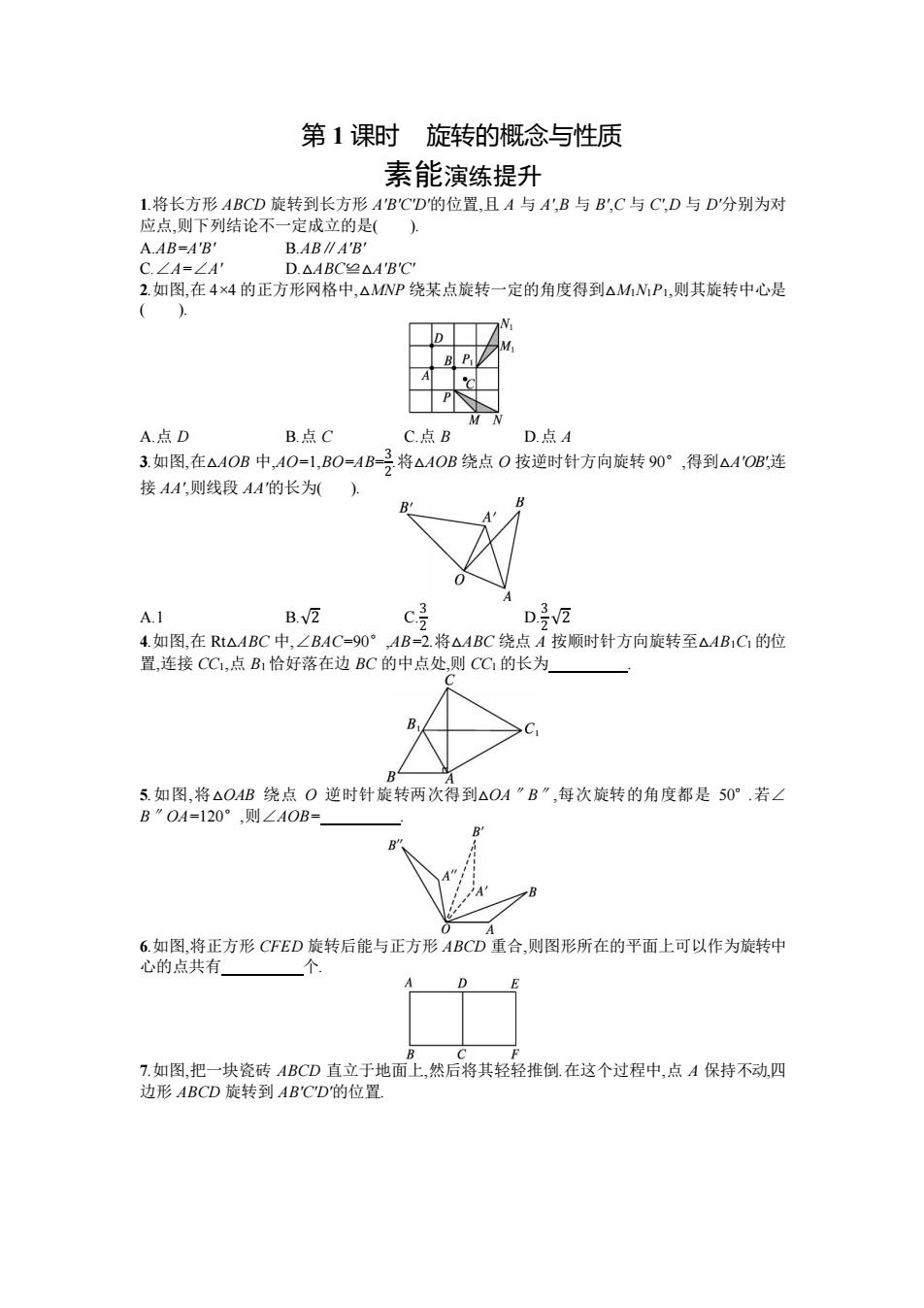
第 1 课时 旋转的概念与性质 素能演练提升 1.将长方形 ABCD 旋转到长方形 A'B'C'D'的位置,且 A 与 A',B 与 B',C 与 C',D 与 D'分别为对 应点,则下列结论不一定成立的是( ). A.AB=A'B' B.AB∥A'B' C.∠A=∠A' D.△ABC≌△A'B'C' 2.如图,在 4×4 的正方形网格中,△MNP 绕某点旋转一定的角度得到△M1N1P1,则其旋转中心是 ( ). A.点 D B.点 C C.点 B D.点 A 3.如图,在△AOB 中,AO=1,BO=AB=3 2 .将△AOB 绕点 O 按逆时针方向旋转 90°,得到△A'OB',连 接 AA',则线段 AA'的长为( ). A.1 B.√2 C. 3 2 D. 3 2 √2 4.如图,在 Rt△ABC 中,∠BAC=90°,AB=2.将△ABC 绕点 A 按顺时针方向旋转至△AB1C1 的位 置,连接 CC1,点 B1 恰好落在边 BC 的中点处,则 CC1 的长为 . 5.如图,将△OAB 绕点 O 逆时针旋转两次得到△OA″B″,每次旋转的角度都是 50°.若∠ B″OA=120°,则∠AOB= . 6.如图,将正方形 CFED 旋转后能与正方形 ABCD 重合,则图形所在的平面上可以作为旋转中 心的点共有 个. 7.如图,把一块瓷砖 ABCD 直立于地面上,然后将其轻轻推倒.在这个过程中,点 A 保持不动,四 边形 ABCD 旋转到 AB'C'D'的位置

D B D (1)指出在这个过程中的旋转中心、旋转方向和旋转角度: (2)指出图中的对应点和对应线段: (3)∠CBA的对应角是
(1)指出在这个过程中的旋转中心、旋转方向和旋转角度; (2)指出图中的对应点和对应线段; (3)∠CBA 的对应角是

【素能演练提升】 1.B2.C3.B4.235.20°6.3 7.解(1)旋转中心是点A,旋转方向是顺时针方向,旋转角度为90°. (2)A,B,C,D的对应点分别是A,B,C,D,AB,AD,BC,CD的对应线段分别是AB,AD',B'C',CD (3)∠CBA
【素能·演练提升】 1.B 2.C 3.B 4.2√3 5.20° 6.3 7.解 (1)旋转中心是点 A,旋转方向是顺时针方向,旋转角度为 90°. (2)A,B,C,D 的对应点分别是 A,B',C',D';AB,AD,BC,CD 的对应线段分别是 AB',AD',B'C',C'D'. (3)∠C'B'A