第一章检测 一、选择题(每小题4分,共32分) 1到三角形三个顶点的距离都相等的点是这个三角形的() A.三条边的垂直平分线的交点 B.三条角平分线的交点 C.三条中线的交点D.三条高的交点 2.如图,己知直线1∥2,将等边三角形如图放置,若∠a=38°,则∠B等于(). A.22° B.17° C.27 D.32° 3.用反证法证明“在同一平面内,若a⊥c,b⊥c,则a∥b时,应假设(). A.a不垂直于cB.a,b都不垂直于c C.a⊥b D.a与b相交 4.如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠ C+∠BAC=145°,则∠EDC的度数为( B C D A.17.5 B.12.5° C.12 D.10° 5.下列定理不存在逆定理的是( A角平分线上的点到这个角两边的距离相等 B.在一个三角形中,等边对等角 C.同位角相等,两直线相平行 D.全等三角形的对应角相等 6.如图,等边三角形ABC的内角平分线相交于点O,过点O分别作△ABC两边AB,AC的平行 线交BC于点D,E,则这个图形中的等腰三角形共有(). B D E A.4个 B.5个 C.6个 D.7个 7.己知等腰三角形的一边长等于4,一边长等于9,则它的周长为( ) A.9 B.17或22 C.17 D.22 8.如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形.连接AE和CD,AE分别交 CD,BD于点M,P,CD交BE于点Q.连接PO,BM.下列结论:①△ABE≌△DBC,②∠ DMA=60°;③△BPQ为等边三角形:,④MB平分∠AMC.其中正确的结论有() 、ME A.4个 B.3个 C.2个 D.1个 二、填空题(每小题4分,共24分) 9.如图,依据尺规作图的痕迹,计算∠α=
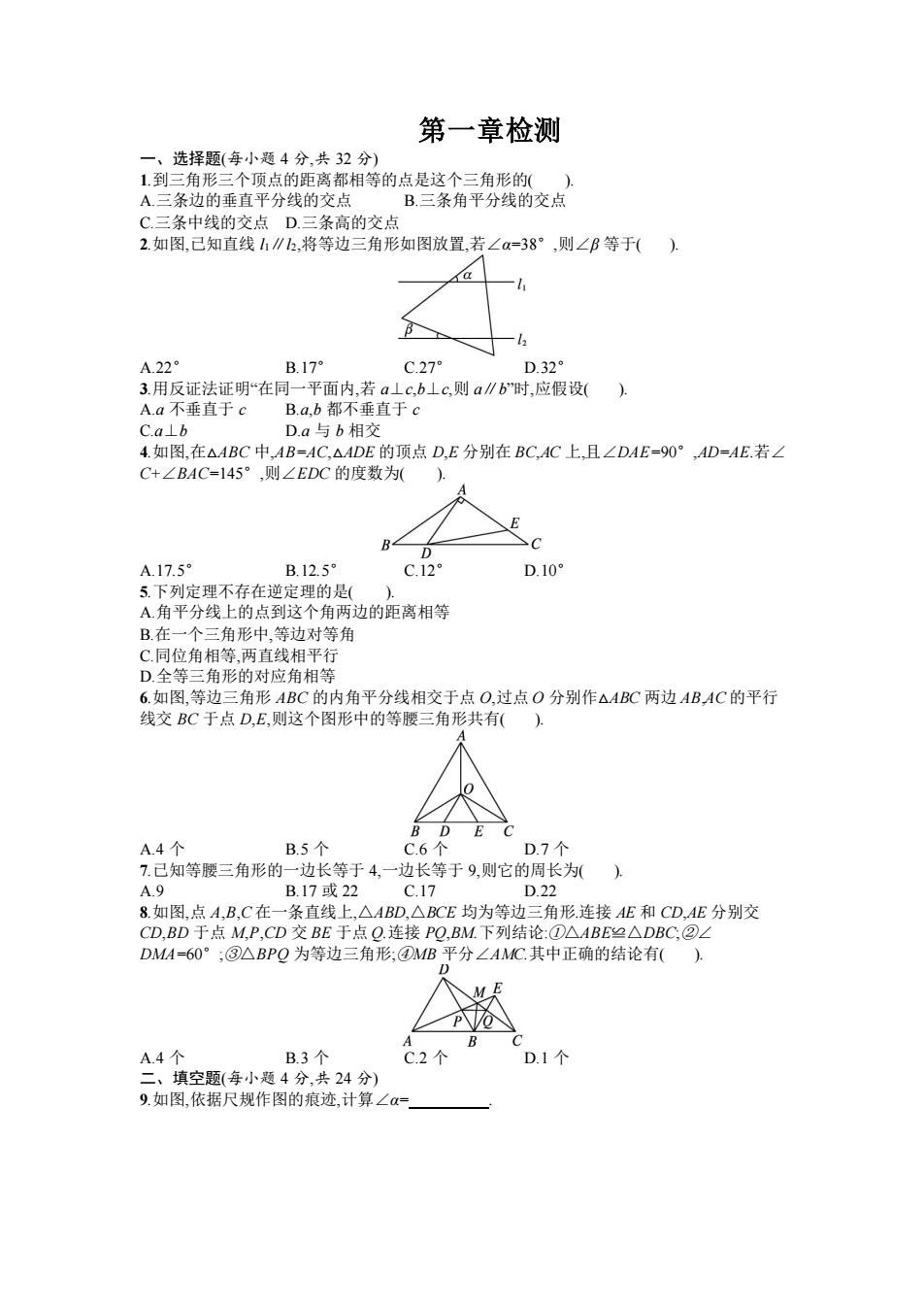
第一章检测 一、选择题(每小题 4 分,共 32 分) 1.到三角形三个顶点的距离都相等的点是这个三角形的( ). A.三条边的垂直平分线的交点 B.三条角平分线的交点 C.三条中线的交点 D.三条高的交点 2.如图,已知直线 l1∥l2,将等边三角形如图放置,若∠α=38°,则∠β 等于( ). A.22° B.17° C.27° D.32° 3.用反证法证明“在同一平面内,若 a⊥c,b⊥c,则 a∥b”时,应假设( ). A.a 不垂直于 c B.a,b 都不垂直于 c C.a⊥b D.a 与 b 相交 4.如图,在△ABC 中,AB=AC,△ADE 的顶点 D,E 分别在 BC,AC 上,且∠DAE=90°,AD=AE.若∠ C+∠BAC=145°,则∠EDC 的度数为( ). A.17.5° B.12.5° C.12° D.10° 5.下列定理不存在逆定理的是( ). A.角平分线上的点到这个角两边的距离相等 B.在一个三角形中,等边对等角 C.同位角相等,两直线相平行 D.全等三角形的对应角相等 6.如图,等边三角形 ABC 的内角平分线相交于点 O,过点 O 分别作△ABC 两边 AB,AC 的平行 线交 BC 于点 D,E,则这个图形中的等腰三角形共有( ). A.4 个 B.5 个 C.6 个 D.7 个 7.已知等腰三角形的一边长等于 4,一边长等于 9,则它的周长为( ). A.9 B.17 或 22 C.17 D.22 8.如图,点 A,B,C 在一条直线上,△ABD,△BCE 均为等边三角形.连接 AE 和 CD,AE 分别交 CD,BD 于点 M,P,CD 交 BE 于点 Q.连接 PQ,BM.下列结论:①△ABE≌△DBC;②∠ DMA=60°;③△BPQ 为等边三角形;④MB 平分∠AMC.其中正确的结论有( ). A.4 个 B.3 个 C.2 个 D.1 个 二、填空题(每小题 4 分,共 24 分) 9.如图,依据尺规作图的痕迹,计算∠α=
g 68 B 10.如图,已知直线1∥2,含30°角的三角板的直角顶点C在1上,30°角的顶点A在2上,如 果边AB与h的交点D是AB的中点,那么∠1= 度 .4 11.如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD于点D,∠ADB=∠C若P是 边BC上一动点,则DP长的最小值为 B 12.如图,点B在AC上,点D在CE上,AD=BD=BC,∠ACE=25°,∠ADE=」 B C I3.做如下操作:在等腰三角形ABC中,AB=ACAD平分∠BAC,交BC于点D.将△ABD作关于 直线AD的轴对称变换,所得的图形与△ACD重合 对于下列结论:①在同一个三角形中,等角对等边:②在同一个三角形中,等边对等角;③等腰三 角形的顶角平分线、底边上的中线和高线互相重合 由上述操作可得出的正确结论是 (填序号) B Di C 14.如图,线段AB,BC的垂直平分线1,32相交于点O,若∠1-39°,则∠AOC- 11 0 三、解答题(共44分) 15.(8分)如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN若 MW=5,求OM的长度. O M N B
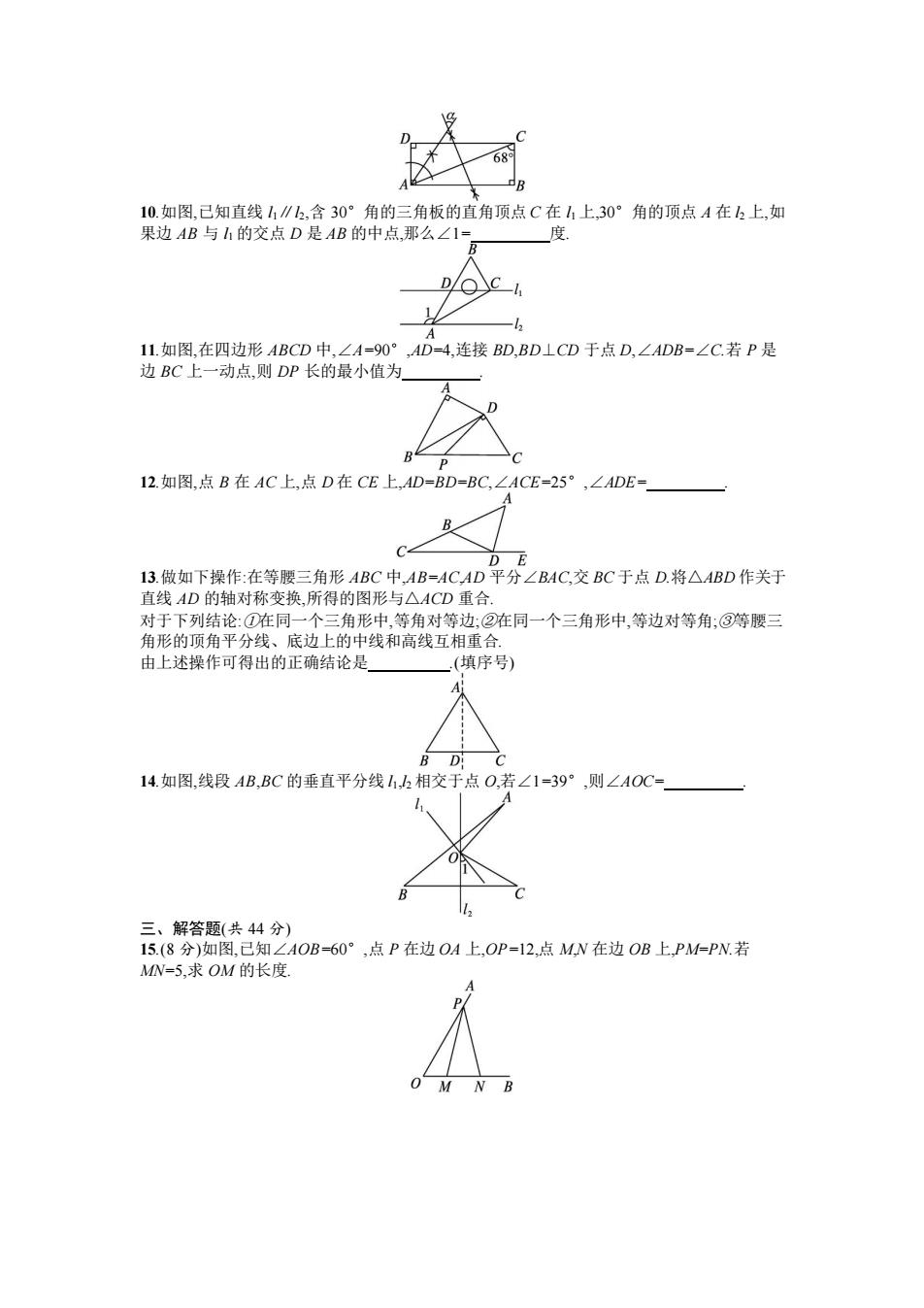
10.如图,已知直线 l1∥l2,含 30°角的三角板的直角顶点 C 在 l1 上,30°角的顶点 A 在 l2 上,如 果边 AB 与 l1 的交点 D 是 AB 的中点,那么∠1= 度. 11.如图,在四边形 ABCD 中,∠A=90°,AD=4,连接 BD,BD⊥CD 于点 D,∠ADB=∠C.若 P 是 边 BC 上一动点,则 DP 长的最小值为 . 12.如图,点 B 在 AC 上,点 D 在 CE 上,AD=BD=BC,∠ACE=25°,∠ADE= . 13.做如下操作:在等腰三角形 ABC 中,AB=AC,AD 平分∠BAC,交 BC 于点 D.将△ABD 作关于 直线 AD 的轴对称变换,所得的图形与△ACD 重合. 对于下列结论:①在同一个三角形中,等角对等边;②在同一个三角形中,等边对等角;③等腰三 角形的顶角平分线、底边上的中线和高线互相重合. 由上述操作可得出的正确结论是 .(填序号) 14.如图,线段 AB,BC 的垂直平分线 l1,l2 相交于点 O,若∠1=39°,则∠AOC= . 三、解答题(共 44 分) 15.(8 分)如图,已知∠AOB=60°,点 P 在边 OA 上,OP=12,点 M,N 在边 OB 上,PM=PN.若 MN=5,求 OM 的长度

16.(8分)如图,在△ABC中,AB=AC.小聪同学利用直尺和圆规完成了如下操作: E D ①作∠BAC的平分线AM交BC于点D: ②作边AB的垂直平分线EF,EF与AM相交于点P: ③连接PB,PC 请你观察图形解答下列问题: (1)线段PA,PB,PC之间的数量关系是 (2)若∠ABC=70°,求∠BPC的度数. 17.(8分)如图,在等腰三角形ABC中,AB=AC,点D,E分别在边AB,AC上,且AD=AE,连接 BE,CD,交于点F (I)判断∠ABE与∠ACD的数量关系,并说明理由; (2)求证:过点A,F的直线垂直平分线段BC
16.(8 分)如图,在△ABC 中,AB=AC.小聪同学利用直尺和圆规完成了如下操作: ①作∠BAC 的平分线 AM 交 BC 于点 D; ②作边 AB 的垂直平分线 EF,EF 与 AM 相交于点 P; ③连接 PB,PC. 请你观察图形解答下列问题: (1)线段 PA,PB,PC 之间的数量关系是 ; (2)若∠ABC=70°,求∠BPC 的度数. 17.(8 分)如图,在等腰三角形 ABC 中,AB=AC,点 D,E 分别在边 AB,AC 上,且 AD=AE,连接 BE,CD,交于点 F. (1)判断∠ABE 与∠ACD 的数量关系,并说明理由; (2)求证:过点 A,F 的直线垂直平分线段 BC

18.(10分)如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分∠ABC交AC于点 E,过点E作EF∥BC交AB于点F (1)若∠C=36°,求∠BAD的度数: (2)求证:FB=FE. 19.(10分)如图,在等边三角形ABC中,∠ABC,∠ACB的平分线交于点O,OB和OC的垂直平 分线交BC于点E,F试探索BE,EF,FC的大小关系,并说明理由
18.(10 分)如图,在△ABC 中,AB=AC,D 是 BC 边上的中点,连接 AD,BE 平分∠ABC 交 AC 于点 E,过点 E 作 EF∥BC 交 AB 于点 F. (1)若∠C=36°,求∠BAD 的度数; (2)求证:FB=FE. 19.(10 分)如图,在等边三角形 ABC 中,∠ABC,∠ACB 的平分线交于点 O,OB 和 OC 的垂直平 分线交 BC 于点 E,F.试探索 BE,EF,FC 的大小关系,并说明理由

第一章检测 一、选择题 1A2.A3.D4.D5.D6.D7.D 8.A 二、填空题 9.56°10.12011.412.75°13.②③ 14.78 三、解答题 15.解如图,过点P作PH⊥MN于点H MH N :∠AOB=60° :∠OPH=30 0H-20P=6 :PM=PN,PH⊥MN,MN=5, .MH=NH=2.5. .:OM=OH-MH=3.5. 16.解(1)PA=PB=PC (2):AM平分∠BAC,AB=AC,∠ABC=70°, .:AD⊥BC,∠BAD=∠CAD=90°-∠ABC=20° :EF是线段AB的垂直平分线, ..PA=PB .:∠PBA=∠PAB=20° :∠BPD是△PAB的外角」 .:∠BPD=∠PAB+∠PBA=40° :PB=PC,PD⊥BC .:∠BPD=∠CPD=40 .:∠BPC=∠BPD+∠CPD=8O 17.(1)解∠ABE=∠ACD.理由如下: ·AB=AC,∠BAE=∠CAD,AE=AD, :△ABE≌△ACD. :∠ABE=∠ACD. (2)证明:AB=AC :∠ABC=∠ACB. 由(I)可知∠ABE=∠ACD, .:∠FBC=∠FCB .FB=FC 又:AB=AC,:点A,F均在线段BC的垂直平分线上,即过点A,F的直线垂直平分线段BC 18.(1)解:AB=AC,:∠C=∠ABC :‘∠C=36°,:∠ABC-36° :'BD=CD,AB=AC, AD⊥BC .:∠ADB=90 .:∠BAD=90°-36°=54° (2)证明·BE平分∠ABC, :∠ABE=LCBE3∠ABC :EF∥BC
第一章检测 一、选择题 1.A 2.A 3.D 4.D 5.D 6.D 7.D 8.A 二、填空题 9.56° 10.120 11.4 12.75° 13.②③ 14.78° 三、解答题 15.解 如图,过点 P 作 PH⊥MN 于点 H. ∵∠AOB=60°, ∴∠OPH=30°. ∴OH=1 2 OP=6. ∵PM=PN,PH⊥MN,MN=5, ∴MH=NH=2.5. ∴OM=OH-MH=3.5. 16.解 (1)PA=PB=PC. (2)∵AM 平分∠BAC,AB=AC,∠ABC=70°, ∴AD⊥BC,∠BAD=∠CAD=90°-∠ABC=20°. ∵EF 是线段 AB 的垂直平分线, ∴PA=PB. ∴∠PBA=∠PAB=20°. ∵∠BPD 是△PAB 的外角, ∴∠BPD=∠PAB+∠PBA=40°. ∵PB=PC,PD⊥BC, ∴∠BPD=∠CPD=40°. ∴∠BPC=∠BPD+∠CPD=80°. 17.(1)解 ∠ABE=∠ACD.理由如下: ∵AB=AC,∠BAE=∠CAD,AE=AD, ∴△ABE≌△ACD. ∴∠ABE=∠ACD. (2)证明 ∵AB=AC, ∴∠ABC=∠ACB. 由(1)可知∠ABE=∠ACD, ∴∠FBC=∠FCB. ∴FB=FC. 又∵AB=AC,∴点 A,F 均在线段 BC 的垂直平分线上,即过点 A,F 的直线垂直平分线段 BC. 18.(1)解 ∵AB=AC,∴∠C=∠ABC. ∵∠C=36°,∴∠ABC=36°. ∵BD=CD,AB=AC, ∴AD⊥BC, ∴∠ADB=90°, ∴∠BAD=90°-36°=54°. (2)证明 ∵BE 平分∠ABC, ∴∠ABE=∠CBE=1 2∠ABC. ∵EF∥BC

.:∠FEB=∠CBE, :∠FBE=∠FEB, ..FB=FE. 19.解BE=EF=FC.理由如下: :△ABC是等边三角形 .:∠ABC=∠ACB=60° :CO,BO分别平分∠ACB,∠ABC, .:∠OBE=∠OCF=30 :EG,HF分别垂直平分OB,OC, ..OE=BE.OF=FC. .:∠BOE=∠OBE-30°, ∠COF=∠OCF=30° .:∠OEF=∠OFE-60°. .:∠EOF=60° ,:△OEF是等边三角形 ..OF=OE=EF. ..BE=EF=FC
∴∠FEB=∠CBE, ∴∠FBE=∠FEB, ∴FB=FE. 19.解 BE=EF=FC.理由如下: ∵△ABC 是等边三角形, ∴∠ABC=∠ACB=60°. ∵CO,BO 分别平分∠ACB,∠ABC, ∴∠OBE=∠OCF=30°. ∵EG,HF 分别垂直平分 OB,OC, ∴OE=BE,OF=FC. ∴∠BOE=∠OBE=30°, ∠COF=∠OCF=30°. ∴∠OEF=∠OFE=60°. ∴∠EOF=60°. ∴△OEF 是等边三角形. ∴OF=OE=EF. ∴BE=EF=FC