第2课时 直角三角形全等的判定 素能演练提升 1.如图,∠C=∠D=90°,添加一个条件,可使用HL”判定Rt△ABC与Rt△ABD全等.以下给出 的条件:①∠ABC=∠ABD,②AC=AD:③BC=BD,④∠BAC=∠BAD.合适的有() B A.1个 B.2个 C.3个 D.4个 2.如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD和CE交于点O,AO的延长线 交BC于点F,则图中全等的直角三角形共有() A.3对 B.4对 C.5对 D.6对 3.如图,在△ABC中,∠BAC=90°,AB=AC,AE是经过点A的一条直线,且B,C在AE的两侧BD ⊥AE于点D,CE⊥AE于点E,CE=2,BD=6,则DE的长为(). A.2 B.3 C.5 D.4 4.如图,在Rt△ABC和Rt△EDF中,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个条 件 ,使RtAABC和Rt△EDF全等. C 5.如图,直线MN∥PQ,AB⊥PQ于点B,点A,D,B,C分别在直线MN与PQ上,点E在AB 上,AD+BC=7,AD=EB,DE=EC,则AB= A D M P —0 6.如图,在△ABC中,AB=CB,∠ABC-90°,点F为AB延长线上一点,点E在BC上,且AE=CF (I)求证:Rt△ABE≌Rt△CBF: (2)若∠CAE=30°,求∠ACF的度数
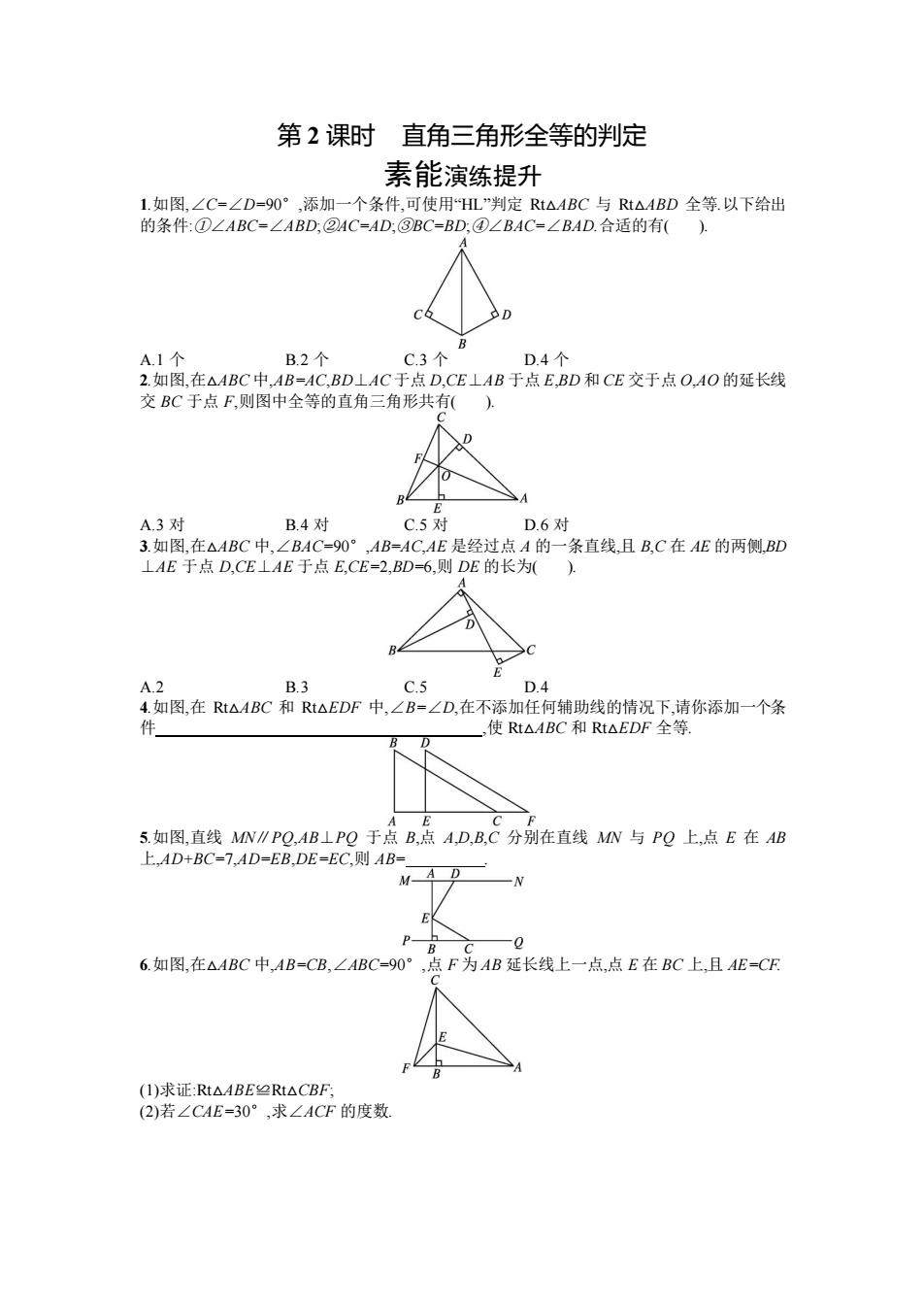
第 2 课时 直角三角形全等的判定 素能演练提升 1.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定 Rt△ABC 与 Rt△ABD 全等.以下给出 的条件:①∠ABC=∠ABD;②AC=AD;③BC=BD;④∠BAC=∠BAD.合适的有( ). A.1 个 B.2 个 C.3 个 D.4 个 2.如图,在△ABC 中,AB=AC,BD⊥AC 于点 D,CE⊥AB 于点 E,BD 和 CE 交于点 O,AO 的延长线 交 BC 于点 F,则图中全等的直角三角形共有( ). A.3 对 B.4 对 C.5 对 D.6 对 3.如图,在△ABC 中,∠BAC=90°,AB=AC,AE 是经过点 A 的一条直线,且 B,C 在 AE 的两侧,BD ⊥AE 于点 D,CE⊥AE 于点 E,CE=2,BD=6,则 DE 的长为( ). A.2 B.3 C.5 D.4 4.如图,在 Rt△ABC 和 Rt△EDF 中,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个条 件 ,使 Rt△ABC 和 Rt△EDF 全等. 5.如图,直线 MN∥PQ,AB⊥PQ 于点 B,点 A,D,B,C 分别在直线 MN 与 PQ 上,点 E 在 AB 上,AD+BC=7,AD=EB,DE=EC,则 AB= . 6.如图,在△ABC 中,AB=CB,∠ABC=90°,点 F 为 AB 延长线上一点,点 E 在 BC 上,且 AE=CF. (1)求证:Rt△ABE≌Rt△CBF; (2)若∠CAE=30°,求∠ACF 的度数

【素能·演练提升】 1.B2.D3.D 4.AB=ED(或BC=DF或AC=EF或AE=CF) 5.7 6.(1)证明∠ABC=90°,:∠CBF=∠ABE=90°, 在Rt△ABE和Rt△CBF中 AE=CFAB=CB. .:Rt△ABE≌Rt△CBF(HL). (2)解:AB=CB,∠ABC-90° .:∠CAB=∠ACB=45° :‘∠BAE=∠CAB-∠CAE=45°-30°=15°. 由(I)知Rt△ABE≌Rt△CBF .:∠BCF=∠BAE=15° .:∠ACF=∠BCF+∠ACB=15°+45°=60°
【素能·演练提升】 1.B 2.D 3.D 4.AB=ED(或 BC=DF 或 AC=EF 或 AE=CF) 5.7 6.(1)证明 ∵∠ABC=90°,∴∠CBF=∠ABE=90°. 在 Rt△ABE 和 Rt△CBF 中, ∵AE=CF,AB=CB, ∴Rt△ABE≌Rt△CBF(HL). (2)解 ∵AB=CB,∠ABC=90°, ∴∠CAB=∠ACB=45°. ∵∠BAE=∠CAB-∠CAE=45°-30°=15°. 由(1)知 Rt△ABE≌Rt△CBF, ∴∠BCF=∠BAE=15°. ∴∠ACF=∠BCF+∠ACB=15°+45°=60°