第3课时等腰三角形的判定与反证法 1四张形状不同的纸片如图所示,用剪刀沿一条直线将它们分别剪开(只允许剪一次),不能得 到两个等腰三角形纸片的是 () 4700 35>B 70°30B A B 27.5 420 -8 人70° 20° B D 2.在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠ACD交AB于点E,则下列结论一定 成立的是( A.BC=EC B.EC=BE C.BC=BE D.AE=EC 3.如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE 的度数为( D A.50° B.51° C.51.5° D.52.5 4.用反证法证明:在一个三角形中,如果两个角不相等,那么它们所对的边也不相等 5.如图,∠BAC=∠ABD,AC=BD,点O是AD,BC的交点,点E是AB的中点试判断OE和AB的 位置关系,并给出证明
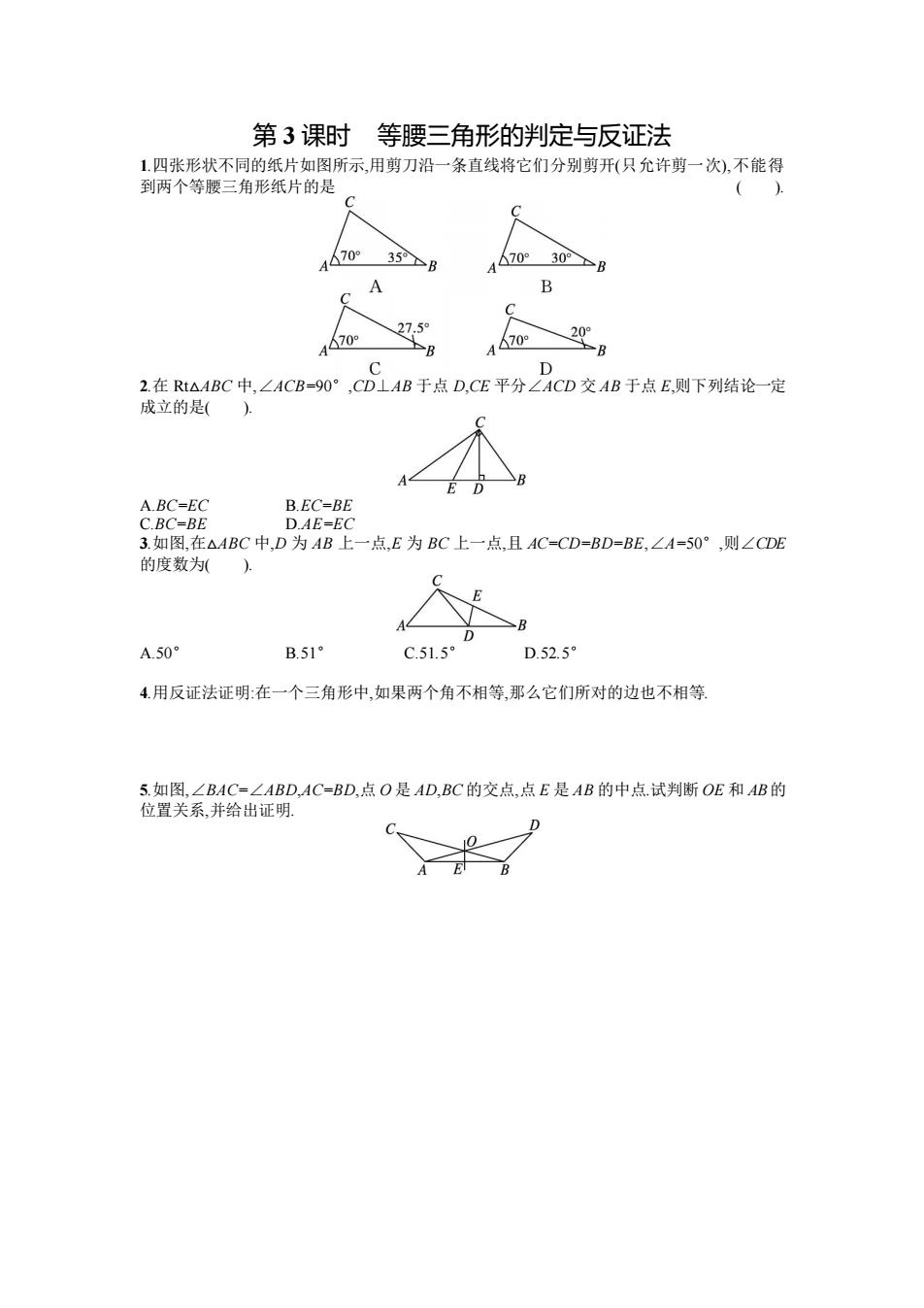
第 3 课时 等腰三角形的判定与反证法 1.四张形状不同的纸片如图所示,用剪刀沿一条直线将它们分别剪开(只允许剪一次),不能得 到两个等腰三角形纸片的是 ( ). 2.在 Rt△ABC 中,∠ACB=90°,CD⊥AB 于点 D,CE 平分∠ACD 交 AB 于点 E,则下列结论一定 成立的是( ). A.BC=EC B.EC=BE C.BC=BE D.AE=EC 3.如图,在△ABC 中,D 为 AB 上一点,E 为 BC 上一点,且 AC=CD=BD=BE,∠A=50°,则∠CDE 的度数为( ). A.50° B.51° C.51.5° D.52.5° 4.用反证法证明:在一个三角形中,如果两个角不相等,那么它们所对的边也不相等. 5.如图,∠BAC=∠ABD,AC=BD,点 O 是 AD,BC 的交点,点 E 是 AB 的中点.试判断 OE 和 AB 的 位置关系,并给出证明

【素能演练提升】 1.B2.C3.D 4.证明假设在一个三角形中,这两个角所对的边相等,那么根据等边对等角,它们所对的两个 角也相等,这与已知条件相矛盾,所以假设不成立.因此,在一个三角形中,如果两个角不相等,那 么它们所对的边也不相等】 5.解OE⊥AB.证明如下: 在△BAC和△ABD中, :AC=BD,∠BAC=∠ABD,AB=BA, .:△BAC≌△ABD(SAS). .·∠OBA=∠OAB ..OA=OB. 又:"AE=BE .OE⊥AB
【素能·演练提升】 1.B 2.C 3.D 4.证明 假设在一个三角形中,这两个角所对的边相等,那么根据等边对等角,它们所对的两个 角也相等,这与已知条件相矛盾,所以假设不成立.因此,在一个三角形中,如果两个角不相等,那 么它们所对的边也不相等. 5.解 OE⊥AB.证明如下: 在△BAC 和△ABD 中, ∵AC=BD,∠BAC=∠ABD,AB=BA, ∴△BAC≌△ABD(SAS). ∴∠OBA=∠OAB. ∴OA=OB. 又∵AE=BE, ∴OE⊥AB