
2019/6/20 本章内容 第3章运输问题 3.1运输问题的数学模型 Transportation Problems 3.2表上作业法 3.3运输问题变形 马俊 3.4指派问题 国际商学院 2019-6-2 3.5运输问题的中转问题 △丝 A图 3.1运输问题的数学模型 简述 石8 单列章的原因在于: 方法对此类型进行求解 用出了赛 本章的重点在:掌提表格化方法求解运输 国B 产地产量 销量销地 A 3.1运输问题的数学模型 运输问线性规划模犁 数学篇器 B1 B2B3 B4 A A型性 1
2019/6/20 1 第3章 运输问题 Transportation Problems 马俊 国际商学院 2019-6-2 本章内容 3.1 运输问题的数学模型 3.2 表上作业法 3.3 运输问题变形 3.4 指派问题 3.5 运输问题的中转问题 • 运输、指派和转运问题,实际上都可以用 LP 模 型加以描述,所以可以认为它们是 LP 的特例 • 单列一章的原因在于:应用面极广,实践性很强, 而特有的数学结构使得人们设计出了特别有效的 方法对此类模型进行求解 • 本章的重点在:掌握表格化方法求解运输 简述 3.1 运输问题的数学模型 11 c 产地 产量 销地 1 a i a ma 1 b j b n b 1 j c i1 c ij c in c mn c mj c m1 c 1n c A1 Ai Am B1 Bj Bn 销量 3.1 运输问题的数学模型 例. 有A1,A2,A3三个砖瓦厂月产量分别为14,27,19 万块,供应B1,B2,B3,B4四个工地,月需要量分别为 22,13,12,13万块,每万块运费如下表,求总运费最 少的方案。 A1 14 A2 27 A3 19 22 13 12 13 B1 B2 B3 B4 6(千元) 7 5 3 8 4 2 7 5 9 10 6 运输问题线性规划模型 x x x x x x x x x x x x 0 x x x 13 x x x 12 x x x 13 x x x 22 x x x x 19 x x x x 27 s.t.x x x x 14 min z 6x 7x 5x 3x 8x 4x 2x 7x 5x 9x 10x 6x 11 12 13 14 21 22 23 24 31 32 33 34 14 24 34 13 23 33 12 22 32 11 21 31 31 32 33 34 21 22 23 24 11 12 13 14 11 12 13 14 21 22 23 24 31 32 33 34 + + = + + = + + = + + = + + + = + + + = + + + = = + + + + + + + + + + + 供 应 地 约 束 需 求 地 约 束

2019/6/20 运输问感模型与性质 运输问题的一般数学模型 ·运输问愿的一般提法:某种物资有若干产地和销 ·有m个产地生产某种物资,有个地区需要该类物资 地,现在需要把这种物资从各个产地运到各个销 ,b.bbn表示各销地 地,产量总数等于销量总数。已知各产地的产量 和各销地的销量以及各产地到各销地的单位运价 min w- ==2n销量约 A性 0 A 运输问惠的特点与性质 ◆矩阵的元素均为1或0: 存获组的矩库具有特珠的结构写出式系 。每一列只有两个元素为1,其余元素均为0: 0.10.0r,其 △世 3.2运输问题的表上作业法 运输问题的表上作业法 表上作业法和单纯形法的求解思想完全一数,但 是具体作法更加简德。 A整 A性 2
2019/6/20 2 运输问题模型与性质 • 运输问题的一般提法: 某种物资有若干产地和销 地,现在需要把这种物资从各个产地运到各个销 地,产量总数等于销量总数。已知各产地的产量 和各销地的销量以及各产地到各销地的单位运价 (或运距),问应如何组织调运,才能使总运费 (或总运输量)最省? 运输问题的一般数学模型 • 有m个产地生产某种物资,有n个地区需要该类物资 • 令a1 , a2 , …, am表示各产地产量, b1 , b2 , …, bn表示各销地 的销量,ai=bj称为产销平衡。 • 设xij表示产地 i 运往销地 j 的物资量,cij表示对应的单位 运费,则我们有运输问题的数学模型如下: = = = = = = = = = 0 1,2, , 1,2, , min 1 1 1 1 ij j m i ij n j ij i m i n j ij ij x x b j n x a i m w c x 销量约束 产地约束 运输问题的特点与性质 约束方程组的系数矩阵具有特殊的结构,写出式系 数矩阵A,形式如下: n n m m mn x , x , , x ; x , x , x , , , , , x , x , x 1 1 1 2 1 2 1 2 2 2 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 m行 n行 ❖ 矩阵的元素均为1或0; ❖ 每一列只有两个元素为1,其余元素均为0; ❖ 列向量Pij =(0,…,0,1,0,…,0,1,0,…0)T,其中 两个元素1分别处于第i行和第m+j行。 3.2 运输问题的表上作业法 (1)单纯形法 (2)表上作业法 由于问题的特殊形式而采用的更简洁、更方 便的方法。 运输问题的表上作业法 表上作业法的基本思想是:先设法给出一个初始方 案,然后根据确定的判别准则对初始方案进行检查、调 整、改进,直至求出最优方案,如图3-1所示。 表上作业法和单纯形法的求解思想完全一致,但 是具体作法更加简捷

2019/6/20 方 定是香 是 初始方案的确定 作业表(产销平衡表) 基本可行解) 初始方案戴是初始基本可行解, 格运输门愿的有关信息表和决策变量—澜运量结 最优方案 合在一起构成“作业表”(产销平衡表)。 表31是两个产地、三个销地的运输问题作业表。 图31运输问思求解思路图 A 例31甲、乙两个煤矿供应A、B、C三个城市用 表31运输间圆作麦(运价麦) 煤,各煤矿产量及各城市需煤量、各煤矿到各城市的 解地 运输距离见下表,求使总运输量最少的调运方案。 B: 产量 运距 城市 产地 A 250 日销量 6 (求量) 100 200 例3-1的数学模型 初始解的确定 mmZ=90x,+70x2+100x+80x1+65x2+752总运输量 1、最小元素法 景小元素法的基本思想是“就近供应”, ,+,+=200 ++=250日产量约束 2、西北角法 西北角法则不考感运距(或运价),年次部 需求约 选余表格的左上角(即西北角)元素作为基变 +5=20 量,其它过程与最小元素法相同 ,20,il2j-l23 A兰
2019/6/20 3 确定初始方案 ( 初 始 基本可行解) 改进调整 (换基迭代) 否 判定是否 最 优? 是 结 束 最优方案 图3-1 运输问题求解思路图 初始方案的确定 作业表(产销平衡表) 初始方案就是初始基本可行解。 将运输问题的有关信息表和决策变量——调运量结 合在一起构成“作业表”(产销平衡表)。 表3-1是两个产地、三个销地的运输问题作业表。 调 销地 运 量 产地 B1 B2 B3 产 量 A1 c11 X11 c12 X12 c13 X13 a1 A2 c21 X21 c22 X22 c23 X23 a2 销 量 b1 b2 b3 = = = 3 1 2 1 j j i i a b 表3-1 运输问题作业表(运价表) 例3-1 甲、乙两个煤矿供应A、B、C三个城市用 煤,各煤矿产量及各城市需煤量、各煤矿到各城市的 运输距离见下表,求使总运输量最少的调运方案。 100 150 200 450 日销量 (需求量) 乙 80 65 75 250 甲 90 70 100 200 日产量 A B C (供应量) 运距 城市 煤矿 例3-1的数学模型 = = + = + = + = + + = + + = = + + + + + 0, 1,2; 1,2,3; 200 150 100 250 200 . . min 90 70 100 80 65 75 1 3 2 3 1 2 2 2 1 1 2 1 2 1 2 2 2 3 1 1 1 2 1 3 1 1 1 2 1 3 2 1 2 2 2 3 x i j x x x x x x x x x x x x st Z x x x x x x ij 需求约束 日产量约束 总运输量 初始解的确定 1、最小元素法 最小元素法的基本思想是“就近供应” ; 2、西北角法 西北角法则不考虑运距(或运价),每次都 选剩余表格的左上角(即西北角)元素作为基变 量,其它过程与最小元素法相同

2019/6/20 用西北角法确定例31初始调运方案 用最小元素法确定例31初始调运方案 调、地 运 B B 产量 B B 产量 1009010-70: -00-280100 10090 79100100260100 A Xu X 80:506520075☐250200 89150第100752Q-100 A X2 100 10:200 销量 100 150 200 50 50 00 40,02 A 最优性检验 (一)闭回路法 检查当前调运方案是不是优方案的过程就是优性 什么是闭回略? 检查的万运 导于零,则该方案就是最优调运方案,否则就应 甲实的护钠的度一条封闭查镜。且所有的边部是水 (一)阳回略法 (二)对得变量法 △世 △世 (一)闭回略法 约定作为起始顶点的非基变量为奇数点1其它 以确定了初始调运方案的作业表为基赠,以一 项点顺次排列,那度,该非基变量x的检验数: 个非基变量作为起始顶点,寻求闭回略。 0,三(闭回略上奇数次顶点运距或运价之和) 可以证明。如果对闭同路的方向不加区别,对 (闭回略上偶囊次顶点运距或运价之和) A性 A性 d
2019/6/20 4 调 销地 运 量 产地 B1 B2 B3 产 量 A1 90 X11 70 X12 100 X13 200 A2 80 X21 65 X22 75 X23 250 销 量 100 150 200 450 用最小元素法确定例3-1初始调运方案 150 100 100 100 100 100 100 调 销地 运 量 产地 B1 B2 B3 产 量 A1 90 X11 70 X12 100 X13 200 A2 80 X21 65 X22 75 X23 250 销 量 100 150 200 450 用西北角法确定例3-1初始调运方案 100 100 100 50 50 200 200 得到初始调运方案为: x11=100,x12=100,x22=50,x23=200 检查当前调运方案是不是最优方案的过程就是最优性 检验。检查的方法:计算非基变量(未填上数值的格, 即空格)的检验数(也称为空格的检验数),若全部 大于等于零,则该方案就是最优调运方案,否则就应 进行调整。 (一)闭回路法 (二)对偶变量法 最优性检验 (一)闭回路法 什么是闭回路? 图中的折线构成一条封闭曲线,且所有的边都是水 平或垂直的; (a) (b) (c) (d) 以确定了初始调运方案的作业表为基础,以一 个非基变量作为起始顶点,寻求闭回路。 该闭回路的特点是:除了起始顶点是非基变量 外,其他顶点均为基变量(对应着填上数值的格)。 可以证明,如果对闭回路的方向不加区别,对 于每一个非基变量而言,以其为起点的闭回路存在 且唯一。 (一)闭回路法 约定作为起始顶点的非基变量为奇数点1 其它 顶点顺次排列,那麽,该非基变量xij的检验数: 现在,在用最小元素法确定例3-1初始调运方案的 基础上,计算非基变量X12的检验数 : ij =(闭回路上奇数次顶点运距或运价之和)- (闭回路上偶数次顶点运距或运价之和) (3-1)
2019/6/20 例31初始调运方案中以X,(为起点的闭回路 非基变量X的检验藏 丽地 ()-() B. 产量 =70+75(100+65)=-20, 10090 非基变量X的检验最: 200 0 15250 =80+100-(90+75)=15. 200 量 450 (二)位势法 例31初始调运方案位势变量对应表 地 B B2 品产 产地 10090 70100100200 6510075250 钠量 100 200450 位势变 △ (二)位势法 方程组的特点: 然后构造下面的方程组: ◆方程个数是mn12+31的 位势变量共有 41+y=G1=90 的券35个 通常称u为第行的位势,称v为第列 4,+y,=c,2=100 (32) ◆初始方室的每一个共变量x对应一个方程一所 42+2=c22=65 在行和列对应的位势变量之和等于该基变量对应的运 (4,+V3=c23=75 距(或运价):u+yFC ◆方程组恰有一个自由变量,可以证明方程组中任 意一个变量均可取作自由变量
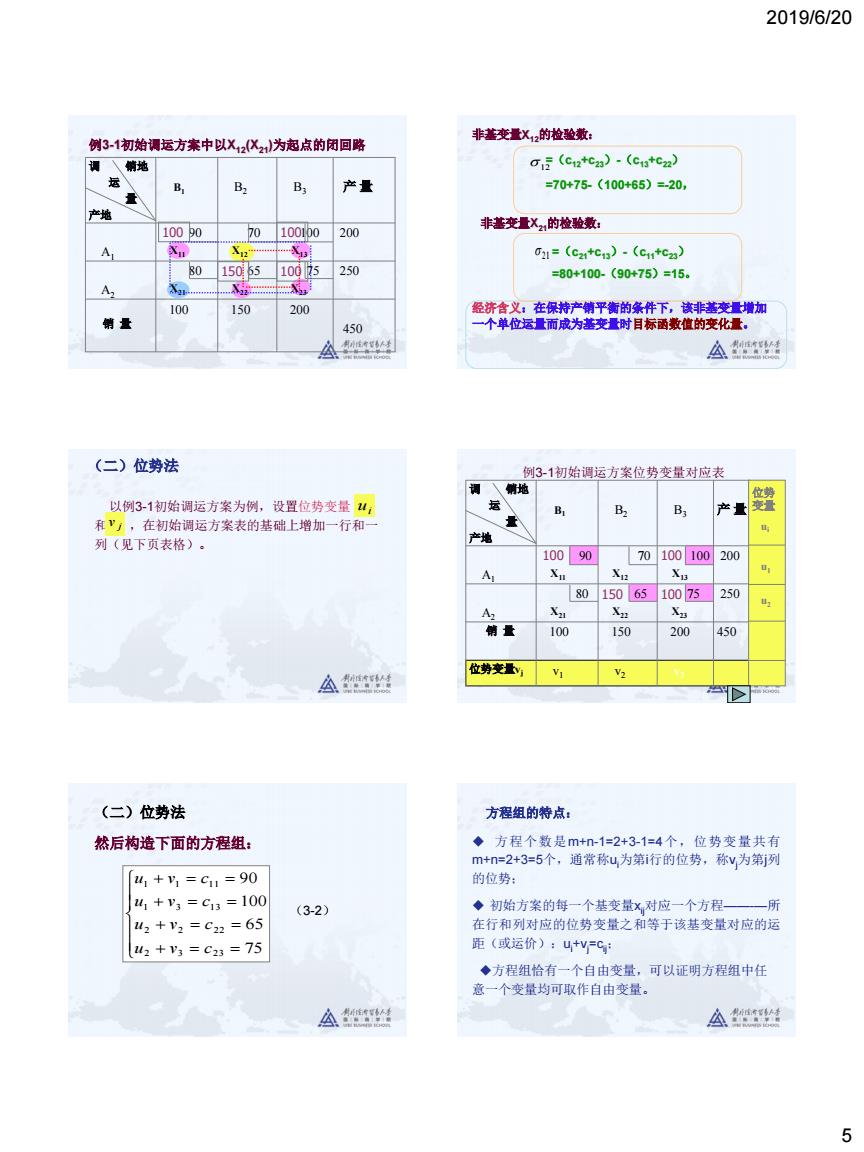
2019/6/20 5 调 销地 运 量 产地 B1 B2 B3 产 量 A1 90 X11 70 X12 100 X13 200 A2 80 X21 65 X22 75 X23 250 销 量 100 150 200 450 100 100 150 100 例3-1初始调运方案中以X12(X21)为起点的闭回路 非基变量X12的检验数: 非基变量X21的检验数: =(c12+c23)-(c13+c22) =70+75-(100+65)=-20, 12 =(c21+c13)-(c11+c23) =80+100-(90+75)=15。 21 经济含义:在保持产销平衡的条件下,该非基变量增加 一个单位运量而成为基变量时目标函数值的变化量。 以例3-1初始调运方案为例,设置位势变量 和 ,在初始调运方案表的基础上增加一行和一 列(见下页表格)。 ui j v (二)位势法 例3-1初始调运方案位势变量对应表 调 销地 运 量 产地 B1 B2 B3 产 量 A1 90 X11 70 X12 100 X13 200 A2 80 X21 65 X22 75 X23 250 销 量 100 150 200 450 位势变量vj v1 v2 v3 100 100 150 100 位势 变量 ui u1 u2 (二)位势法 然后构造下面的方程组: + = = + = = + = = + = = 75 65 100 90 2 3 23 2 2 22 1 3 13 1 1 11 u v c u v c u v c u v c (3-2) 方程组的特点: ◆ 方程个数是m+n-1=2+3-1=4个,位势变量共有 m+n=2+3=5个,通常称ui为第i行的位势,称vj为第j列 的位势; ◆ 初始方案的每一个基变量xij对应一个方程——-—所 在行和列对应的位势变量之和等于该基变量对应的运 距(或运价):ui +vj =cij; ◆方程组恰有一个自由变量,可以证明方程组中任 意一个变量均可取作自由变量

2019/6/20 方案调整 在方程g29军令u83》可解得u,90 (3-3) 若检验数0,小于零,则首先在作业表上以x为虑始 V=100,y225,V2=90,于是 变量作出闭回略,并求出调整量8: 012=C12(u,+y2)=70-(0+90)=-20 =min(该闭回路中得数顶点调运量x】 02=02(2+)=80-(-25+90)=15 与前面用闭回路法求得的结果相同。 A A 魅续上例,因01产-20,面出以x为起始变量的阳国略 地 ·计算调整量:0=Min(100,150)=100 B B 产量 ·按服下面的方法调整调运量: 10090 70100100200 闭回略上,偶数顶点的调运量减去日,奇数顶点 (包括起始顶点)的调运量加上日:闭回略之外的变 量调运量不变, 801505510075250 得到新的调运方来: 100 150 200 量 50 公 A性 销地 销地 B B B. 产量 B 产量 产地 1009010070 100 200 509015070 100200 A X 80 5065 20075 5080 520075250 100 150 200 450 100 150 200 450 藏复上面的步藻,直至求出最优调运方 △丝 A性 6
2019/6/20 6 给定自由变量一个值,解方程组式(3-2),即可 求得位势变量的一组值,根据式(3-1)结合方程组, 推出计算非基变量xij检验数的公式 σij=cij-(ui +vj) (3-3) 在 方程 组 (3 - 2 ) 中 ,令 u1 =0, 则可 解 得 v1 =90, v3 =100,u2 =-25,v2 =90,于是 σ12=c12-(u1 +v2)=70-(0+90)=-20 σ21=c21-(u2 +v1)=80-(-25+90)=15 与前面用闭回路法求得的结果相同。 方案调整 当至少有一个非基变量的检验数是负值时,说明作 业表上当前的调运方案不是最优的,应进行调整。 若检验数σij小于零,则首先在作业表上以xij为起始 变量作出闭回路,并求出调整量θ: ij θ=min{该闭回路中偶数顶点调运量xij} 调 销地 运 量 产地 B1 B2 B3 产 量 A1 90 X11 70 X12 100 X13 200 A2 80 X21 65 X22 75 X23 250 销 量 100 150 200 450 100 100 150 100 1 4 3 2 继续上例,因σ12=-20 ,画出以x12为起始变量的闭回路 • 计算调整量: θ =Min(100,150)=100。 • 按照下面的方法调整调运量: 闭回路上,偶数顶点的调运量减去θ ,奇数顶点 (包括起始顶点)的调运量加上θ ;闭回路之外的变 量调运量不变。 得到新的调运方案: 调 销地 运 量 产地 B1 B2 B3 产 量 A1 90 X11 70 X12 100 X13 200 A2 80 X21 65 X22 75 X23 250 销 量 100 150 200 450 100 100 50 200 重复上面的步骤,直至求出最优调运方案: 调 销地 运 量 产地 B1 B2 B3 产 量 A1 90 X11 70 X12 100 X13 200 A2 80 X21 65 X22 75 X23 250 销 量 100 150 200 450 50 150 50 200

2019/6/20 3.3运输问愿的推广 结果 产销不平衡的运输问题 最优调运方素是: xn=50,×22150,Xm50,xa2200 供大于求◆增加虚报销地 相应的最小总运输量为 Zn=90×50+70×150+80×50+75×200 供不应求→增加虚拟产地 转化 =34000(吨公里) 产销平衡的运输问愿 △ 对应的运距(或运价)? 3.3运输问题的推广 运问应用举例 5 10 15 40 50 产第不平衡→产销平衡 30 30 60 80 70150 25 115603070 A 3.4指派问题 A2 204015 303010 品】 A3 3035 40 52510 A4度)●M0 0020 b25115603070210 1041415 得到这禅的平衡表后,再技根平衡的运输问圆求解模型。 丙9141613 8119 1
2019/6/20 7 结 果 最优调运方案是: x11=50,x12=150,x21=50,x23=200 相应的最小总运输量为: Zmin=90×50+70×150+80×50+75×200 =34000(吨公里) 3.3 运输问题的推广 产销不平衡的运输问题 供大于求 供不应求 增加虚拟销地 增加虚拟产地 产销平衡的运输问题 对应的运距(或运价) ? 转化 3.3 运输问题的推广 产销不平衡 产销平衡 – 供过于求,即 ai > bj ,增加一个虚收点Dn+1, bn+1= ai - bj , 令 wi,n+1=0, i=1,2,…,m – 供小于求,即 ai < bj ,增加一个虚发点Wm+1, am+1= bj - ai , 令 wm+1,j=0, j=1,2,…,n 运输问题应用举例 1 2 3 4 5 10 15 20 20 40 1 15 35 50 20 40 15 30 30 2 10 60 100 30 35 40 55 25 3 80 70 150 25 115 60 30 70 如产地3的产量变为130,又B地区需的115单位必 须满足,试重新确定最优调拨方案 B1 B2 B3 B4 B5 ai A1 10 15 20 20 40 50 A2 20 40 15 30 30 100 A3 30 35 40 55 25 130 A4(虚) 0 M 0 0 0 20 bj 25 115 60 30 70 210 得到这样的平衡表后,再按照平衡的运输问题求解模型。 3.4 指派问题 例3-2 有一份中文产品说明书需译成英、日、德、俄四种 语言,现有甲、乙、丙、丁四人都可以胜任,他们译 成不同语言所需时间不同,如下表。求如何分配使所 需总时间最少(每人只译一种) 语言 人员 E J G R 甲 2 15 13 4 乙 10 4 14 15 丙 9 14 16 13 丁 7 8 11 9 整数规划

2019/6/20 3.4指派间题(assignment problem) 例32意立横遥 看第项工作交与个人完成 指深问题的标准形式及其数学棋型 【。无第项工作不交与衡个人完城 指派问题的标准形式(以人和事为例)是: 有n个人和n件事,已知第i人做第j 译英文 甲:++ Cj=1, 这件率的总费用最少.如例32 0域1-234P23, 公包 A幻 一般模型 匈牙利解法 潮深同的标准形式,令 标准的指派问题是一类特的01整数规划问 大-日深个光盘务 题,可以用多种相应的解法来求解。但是, 都没有充分利用指派问愿的特殊性质来有效减少计算 量,1955年,库愿(W.W.Kuhn)利用甸牙利数学家 minz=ic 康尼格(D.K6nig)的关于矩阵中独立零元素的定理, 1,j=1,2,,n 提出了指派问愿的一种解法,由此,习惯上称之为图 牙利解法。 公 Ag兰 匈牙利解法 匈牙利解法的一般步骤 步课一:变换系数矩阵。使其年行及年列至少有一 甸牙利解法的关键是利用了指派问题最优解的 个零元素,同时不出现负元素。 如下性质: 步硬二:进行试指派,即确定独立零元素。 若从指派问题的系数矩阵C=(c1)nXn的 步骤三:继线变换系数矩阵,然后返回步骤二, 某行(或某列)各元素分别减去一个常囊k,得到 个新的系数矩阵C'=(c,)则以C和C为系数矩 阵的两个指派问愿有相同的最优解。 A △g 8
2019/6/20 8 43 指派问题的标准形式及其数学模型 指派问题的标准形式(以人和事为例)是: 有 n 个人和 n 件事,已知第 i 人做第 j 事 的费用为 Cij(i,j = 1,2,…,n),要求确 定人和事之间的一一对应的指派方案,使完成 这件事的总费用最少。如例3-2. 3.4 指派问题(assignment problem) 例3-2 建立模型: 设 xij= 1 0 译英文: x11+ x12 + x13 + x14 =1 译日文: x21+ x22 + x23 + x24 =1 译德文: x31+ x32 + x33 + x34 =1 译俄文: x41+ x42 + x43 + x44 =1 甲: x11+ x21 + x31 + x41 =1 乙: x12+ x22 + x32 + x42 =1 丙: x13+ x23 + x33 + x43 =1 丁: x14+ x24 + x34 + x44 =1 xij =0或1 (i=1,2,3,4; j=1,2,3,4) Min z= aijxij (aij---效率) i=1j=1 4 4 若第i项工作交与第j个人完成 若第i项工作不交与第j个人完成 45 一般模型 指派问题的标准形式,令 1 当指派第 i 人完成第 j 项任务 0 当不指派第 i 人完成第 j 项任务 xij = min z = ∑∑cijxij ∑xij = 1, j = 1,2,…,n ∑xij = 1, i = 1,2,…,n xij = 1 或 0 46 匈牙利解法 标准的指派问题是一类特殊的 0-1 整数规划问 题,可以用多种相应的解法来求解。但是,这些方法 都没有充分利用指派问题的特殊性质来有效减少计算 量。1955年,库恩(W.W.Kuhn)利用匈牙利数学家 康尼格(D.König)的关于矩阵中独立零元素的定理, 提出了指派问题的一种解法,由此,习惯上称之为匈 牙利解法。 47 匈牙利解法的关键是利用了指派问题最优解的 如下性质: 若从指派问题的系数矩阵 C = ( cij )n×n 的 某行(或某列)各元素分别减去一个常数 k ,得到一 个新的系数矩阵C’ = ( c’ij )则以 C 和 C’ 为系数矩 阵的两个指派问题有相同的最优解。 匈牙利解法 48 步骤一: 变换系数矩阵。使其每行及每列至少有一 个零元素,同时不出现负元素。 步骤二: 进行试指派,即确定独立零元素。 步骤三: 继续变换系数矩阵,然后返回步骤二。 匈牙利解法的一般步骤
2019/6/20 匈牙利解法的一般步骤 指派问题(assignment problem) 以例3-2说明步: 指(assignment problem) 151 013112 01370 0101 0101 06 c'a 0574 53 811 0142 0142 604 指派问题(assignment problem) 指派问题(assignment problem) 以例32说弱步雕 食 0001 0100 () 000 比时如通0元素的 个数口 =n=4,所以得到最优解 0010 A 指派问题(assignment problem) 非标准形式的指派问题 匈牙利解法的一般步臻 其方法幕在未劫言雄兰 用中,常会到各种 的元素中找出 元。松后在打号行各元 式,然后再用1 都减去这一最小元素,而在打号列的各元豪都加上 中最大 素为m 这一最小元素,以保正原来的0元素不变。这样得到 新系数矩阵(其最优解和原问题相同)。若得到门个 数立的0元素,则已得最优解,否则重复该步票继续 变换系数矩阵。 9
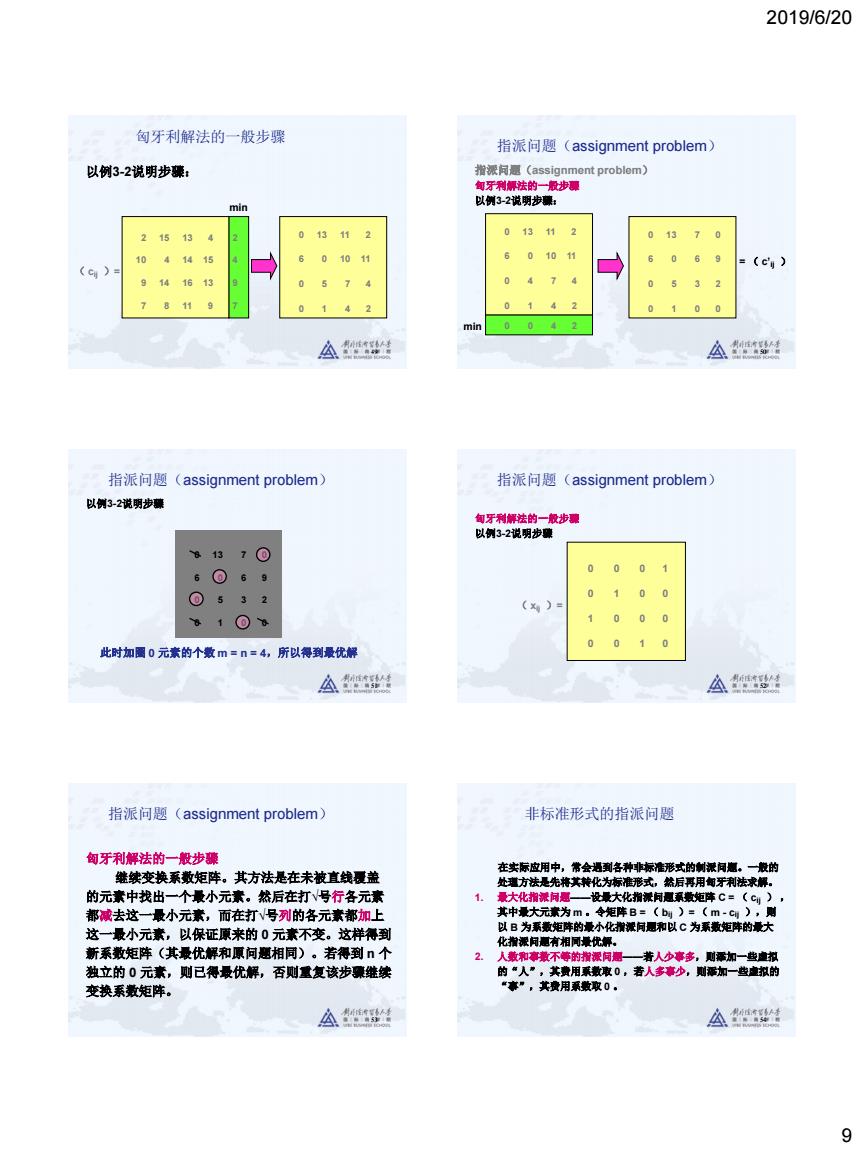
2019/6/20 9 49 以例3-2说明步骤: 2 15 13 4 10 4 14 15 9 14 16 13 7 8 11 9 0 13 11 2 6 0 10 11 0 5 7 4 0 1 4 2 2 4 9 7 min ( cij )= 匈牙利解法的一般步骤 50 指派问题(assignment problem) 匈牙利解法的一般步骤 以例3-2说明步骤: 0 13 11 2 6 0 10 11 0 4 7 4 0 1 4 2 min 0 0 4 2 0 13 7 0 6 0 6 9 0 5 3 2 0 1 0 0 = ( c’ij ) 指派问题(assignment problem) 51 以例3-2说明步骤 0 13 7 0 6 0 6 9 0 5 3 2 0 1 0 0 此时加圈 0 元素的个数 m = n = 4,所以得到最优解 指派问题(assignment problem) 52 匈牙利解法的一般步骤 以例3-2说明步骤 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 ( xij )= 指派问题(assignment problem) 53 匈牙利解法的一般步骤 继续变换系数矩阵。其方法是在未被直线覆盖 的元素中找出一个最小元素。然后在打√号行各元素 都减去这一最小元素,而在打√号列的各元素都加上 这一最小元素,以保证原来的 0 元素不变。这样得到 新系数矩阵(其最优解和原问题相同)。若得到 n 个 独立的 0 元素,则已得最优解,否则重复该步骤继续 变换系数矩阵。 指派问题(assignment problem) 54 在实际应用中,常会遇到各种非标准形式的制派问题。一般的 处理方法是先将其转化为标准形式,然后再用匈牙利法求解。 1. 最大化指派问题——设最大化指派问题系数矩阵 C = ( cij ) , 其中最大元素为 m 。令矩阵 B = ( bij )= ( m - cij ),则 以 B 为系数矩阵的最小化指派问题和以 C 为系数矩阵的最大 化指派问题有相同最优解。 2. 人数和事数不等的指派问题——若人少事多,则添加一些虚拟 的“人”,其费用系数取 0 ,若人多事少,则添加一些虚拟的 “事”,其费用系数取 0 。 非标准形式的指派问题

2019/6/20 非标准形式的指派问题 3.5运输向题的中转向题 非标准形式的湘同愿 该人化作肌叫 价以 例8.、腾飞电子公司在大连和广州 6 来不 岛较适,公司同意大连分厂向青岛直 A性 3.5运榆向题的中转问题 3.5远输向题的中转问题 新公得置 器:凝 先公:赞 在之。电之 △性 3.5远榆问题的中转向题 3.5远输间题的中转向题 扩大的给产平与运价表】 M 2 S M 品 2.运给表中不可能方名的运取 作M自身对白身的试为0, 、对干最使方名。其中气,为身时身的运量,实际上性 A性 70
2019/6/20 10 55 非标准形式的指派问题 3. 一个人可做几件事的指派问题——若某个人可以做几件事,则 将该人化作几个“人”来接受指派。这几个“人”做同一件事 的费用系数当然都一样。 4. 某事一定不能由某人做的指派问题——若某事一定不能由某人 做,则可将相应的费用系数取为足够大的数 M 。 非标准形式的指派问题 56 3.5 运输问题的中转问题 在原运输问题上增加若干转运站。运输方式有:产地 → 转运站、转 运站 → 销地、产地 → 产地、产地 → 销地、销地 → 转运站、销地 → 产 地等。 例8、腾飞电子仪器公司在大连和广州 有两个分厂生产同一种仪器,大连分厂 每月生产400台,广州分厂每月生产600 台。该公司在上海和天津有两个销售公 司负责对南京、济南、南昌、青岛四个 城市的仪器供应。另外因为大连距离青 岛较近,公司同意大连分厂向青岛直接 供货,运输费用如图,单位是百元。问应该如何调运仪器, 可使总运输费用最低?图中 1- 广州、2 - 大连、 3 - 上海、4 - 天津、5 - 南京、6 - 济南、7 - 南昌、8 - 青岛 57 解:设 xij 为从 i 到 j 的运输量,可得到有下列特点的线性规划模型: 目标函数:Min f = 所有可能的运输费用(运输单价与运输量乘积之和) 约束条件: 对产地(发点) i :输出量 - 输入量 = 产量 对转运站(中转点):输入量 - 输出量 = 0 对销地(收点) j :输入量 - 输出量 = 销量 例8.(续) 目标函数: Min f = 2x13+ 3x14+ 3x23+ x24+ 4x28 + 2x35+ 6x36+ 3x37+ 6x38+ 4x45+ 4x46+ 6x47+ 5x48 约束条件: s.t. x13+ x14 ≤ 600 (广州分厂供应量限制) x23+ x24+ x28 ≤ 400 (大连分厂供应量限制) -x13- x23 + x35 + x36+ x37 + x38 = 0 (上海销售公司,转运站) -x14- x24 + x45 + x46+ x47 + x48 = 0 (天津销售公司,转运站) x35+ x45 = 200 (南京的销量) x36+ x46 = 150 (济南的销量) x37+ x47 = 350 (南昌的销量) x38+ x48 + x28 = 300 (青岛的销量) xij ≥ 0 , i,j = 1,2,3,4,5,6,7,8 3.5 运输问题的中转问题 58 3.5 运输问题的中转问题 用EXCEL软件求得结果: x13 = 550 x14 =50 ; x23 = 0 x24 = 100 x28 = 300 ; x35 = 200 x36 = 0 x37 = 350 x38 = 0 ; x45 = 0 x46 = 150 x47 = 0 x48 = 0 。 最小运输费用为:4600百元 例9、某公司有A1、 A2、 A3三个分厂生产某种物资,分别供应B1、 B2、 B3、 B4 四个地区的销售公司销售。假设质量相同,有关数据如下表: 试求总费用为最少的调运方案。 假设: 1.每个分厂的物资不一定直接发运到销地,可以从其中几个产地集中一起运; 2.运往各销地的物资可以先运给其中几个销地,再转运给其他销地; 3.除产销地之外,还有几个中转站,在产地之间、销地之间或在产地与销地之 间转运。 B1 B2 B3 B4 产量 A1 3 11 3 10 7 A2 1 9 2 8 4 A3 7 4 10 5 9 销量 3 6 5 6 和=20 59 3.5 运输问题的中转问题 运价如下表: 解:把此转运问题转化为一般运输问题: 1、把所有产地、销地、转运站都同时看作产地和销地; 2、运输表中不可能方案的运费取作M,自身对自身的运费为0; 3、Ai: 产量为 20+原产量, 销量为 20; Ti : 产量、销量均为 20; Bi: 产量为 20, 销量为 20 +原销量,其中20为各点可能变化的最大流量 4、对于最优方案,其中 xi i 为自身对自身的运量,实际上不进行运作。 A1 A2 A3 T1 T2 T3 T4 B1 B2 B3 B4 A1 1 3 2 1 4 3 3 11 3 10 A2 1 --- 3 5 --- 2 1 9 2 8 A3 3 --- 1 --- 2 3 7 4 10 5 T1 2 3 1 1 3 2 2 8 4 6 T2 1 5 --- 1 1 1 4 5 2 7 T3 4 --- 2 3 1 2 1 8 2 4 T4 3 2 3 2 1 2 1 --- 2 6 B1 3 1 7 2 4 1 1 1 4 2 B2 11 9 4 8 5 8 --- 1 2 1 B3 3 2 10 4 2 2 2 4 2 3 B4 10 8 5 6 7 4 6 2 1 3 60 3.5 运输问题的中转问题 扩大的运输问题产销平衡与运价表: A1 A2 A3 T1 T2 T3 T4 B1 B2 B3 B4 产量 A1 0 1 3 2 1 4 3 3 11 3 10 27 A2 1 0 M 3 5 M 2 1 9 2 8 24 A3 3 M 0 1 M 2 3 7 4 10 5 29 T1 2 3 1 0 1 3 2 2 8 4 6 20 T2 1 5 M 1 0 1 1 4 5 2 7 20 T3 4 M 2 3 1 0 2 1 8 2 4 20 T4 3 2 3 2 1 2 0 1 M 2 6 20 B1 3 1 7 2 4 1 1 0 1 4 2 20 B2 11 9 4 8 5 8 M 1 0 2 1 20 B3 3 2 10 4 2 2 2 4 2 0 3 20 B4 10 8 5 6 7 4 6 2 1 3 0 20 销量 20 20 20 20 20 20 20 23 26 25 26 240