本章内容 第6章图与网络优化 6.1图的基本概念 6.2最小支罐树 Graph Theory and 6.3最短路问思 Network Optimization 6.4网络最大流问题 2019-6-3 A A 1736年胶拉将这个间愿抽家 哥尼斯堡七桥问题 婚不出这个面形,聚 终回到原成。 不可在的文中了这是 顶点都与奇数条 相连接 的下名问 碳:豆族责能公失染典备发智七 一笔画问题 A性 △性 6.1图的基本橛念 球队比赛 一结指中的写之间的关联关系 e >端点 >关联点(相邻点) e >关联边(相邻边) A整 A性 1
1 Graph Theory and Network Optimization 第6章 图与网络优化 马 俊 国际商学院 2019-6-3 6.1 图的基本概念 6.2 最小支撑树 6.3 最短路问题 6.4 网络最大流问题 本章内容 B A C D 哥尼斯堡七桥问题 问题:一个散步者能否从任一块陆地出发,走过七 座桥,且每座桥只走过一次,最后回到出发点? 1736年,欧拉将这个问题抽象 成一笔画问题,即能否从某一点开 始不重复地一笔画出这个图形,最 终回到原点。 欧拉在他的论文中证明了这是 不可能的,因为这个图形中每一个 顶点都与奇数条边相连接,不可能 将它一笔画出,这就是古典图论中 的第一个著名问题。 A B C D 一笔画问题 球队比赛 v1 v2 v3 v4 v5 v1 v2 v3 v5 v4 6.1 图的基本概念 • 由m个顶点v1 ,v2 ,…,vm与n条边e1 ,e2 ,…,en,两组基本元素 组成的结构称为图,记为G=(V,E),其中 V={v1 ,v2 ,…,vm},E={e1 ,e2 ,…,en}。 • “结构”指图中的点与边之间的关联关系。 vi e vj k vi vj ek el vh ➢端点 ➢关联点(相邻点) ➢关联边(相邻边)
6.1图的基本橛念 的 之间 带箭头的 叫做 如果 个图是由点和边所构 表示图 区公国 △ △ 无向图例子 有向图的例子 下图是一个无向图G=(W,) 其中y={,gvd E=vl,[vl,[小, [vs.V4],[VV,[vaVa.[va.Va -))(v.(V(V) (VgV ).(vsVj).(vsVD.(vsVo).(VoV) 其中v示有 记作,向的氧 图的分类 周无内图,记作G=心,目 有向图的边 图G或有向图D中的点数,记作pG)或D,简 有向图,记作D=(N, 称为。 例1:香尼斯桥问圆的图为 个无向图, 如果图G中,一条边的两个端点是相同的,事么称 例2:五个球队的比赛情况,V1→V2表示v1胜2 这条边是环,如图中的边[y,Y]是环。 如果两个点之间有两条以上的边,那么称它们为 多量边,如图中的边[v1,[v2】。 一个无环,无多量边的图称为葡单图 一个无环,有多置边的图称为多量图
2 6.1 图的基本概念 • 在一个图中,只要确定了点边关联关系,无论如何改变 顶点的位置,改变边的形状和大小,所得到的新图都与 原图是同一个图,也称为同构。 A B C D A B C D A B C D 图论中的图是由点和点与点之间的联线所组成 的。把点与点之间不带箭头的线叫做边,带箭头的 线叫做弧。 如果一个图是由点和边所构成的,称为无向图, 记作 G =(V,E ),其中V 表示图G 的点集合,E 表 示图G的边集合。连接点 vi ,vjV 的边记作[vi ,vj ], 或者[vj ,vi ]。。 无向图例子 下图是一个无向图 G =(V,E) 其中V ={v1,v2,v3,v4} E={[v1,v2],[v2,v1],[v2,v3], [v3,v4],[v1,v4],[v2,v4],[v3,v3]} v3 v1 v2 v4 如果一个图是由点和弧 所构成的,那么称它为 有向图,记作D =(V, A),其中V 表示有向图 D的点集合,A 表示有 向图D的弧集合。一条 方向从vi指向vj的弧, 记作(vi,vj)。 有向图的例子 下图是一个有向图 D =(V,A ) 其中V={v1 ,v2 ,v3 ,v4 ,v5 ,v6 ,v7} A={(v1 ,v2 ), (v1 ,v3 ), (v3 ,v2 ), (v3 ,v4 ), (v2 ,v4 ), (v4 ,v5 ), (v4 ,v6 ), (v5 ,v3 ), (v5 ,v4 ), (v5 ,v6 ), (v6 ,v7 )} v3 v5 v7 v2 v4 v1 v6 图 无向图,记作G=(V,E) 有向图,记作D=(V,A) 例1:哥尼斯堡桥问题的图为一个无向图。 有向图的边 称为弧。 例2:五个球队的比赛情况, v1 v2 表示v1胜v2。 v1 v2 v3 v4 v5 图的分类 一个图G 或有向图D 中的点数,记作p(G)或p(D), 简 记作p, 边数或者弧数, 记作q(G)或q(D), 简记作q。 先考虑无向图 G =(V,E ) 如果图G 中,一条边的两个端点是相同的,那么称 这条边是环,如图中的边[v3 ,v3]是环。 如果两个点之间有两条以上的边,那么称它们为 多重边,如图中的边[v1,v2],[v2,v1]。 一个无环,无多重边的图称为简单图. 一个无环,有多重边的图称为多重图

链、简单链、韧等链、连通图 以点v为端点的边的个数称为点v的次,记作(W), 链:由两两相第的点及其相关联的边构成的点边序列 次为零的点称为氧立点: 如vg,01,1,2, 次为1的点称为悬挂点: 悬挂点的边称为悬挂边 分别为的惠点 次为奇戴的点称为奇点 前单 次为偶数的点称为俱点。 含的点均不相同 初等、前单 葡单圆:面中所含的边均不相同 A A 连通图:图中任意两点之间均至少 能测作不 有向图相关概念 基遍图:有向图中去掉所有或上的箭头, 很到的于向型 弧:有向图的边a=a,),惠点u,终点Y ,B2sB1,称G2是G的 路:若有从口到v不考虑方向的链,且 各方向一致,则称之为从u到v的略: 初等路:各顶点都不相同的略: 初等回路:u=v的初等略: A △世 无向图中的概念总结 无向图的性质 ,多量边 奇点 ·简单图 偶点 ·多重图 ·环 以下各点能不能是某简单图的项点的次的序列? 初等(单) 悬挂点 初等(简单)圆 悬挂边 连通图 ,孤立点 支撑子图 A性 A丝
3 以点v为端点的边的个数称为点v的次,记作d(v) 。 次为零的点称为弧立点; 次为1的点称为悬挂点; 悬挂点的边称为悬挂边; 次为奇数的点称为奇点; 次为偶数的点称为偶点。 链、简单链、初等链、连通图 链:由两两相邻的点及其相关联的边构成的点边序列; 如v0 ,e1 ,v1 ,e2 , v2 ,e3 ,v3 ,…,vn-1,en , vn ; v0 , vn分别为链的起点和终点 简单链:链中所含的边均不相同 初等链:链中所含的点均不相同 圈、初等圈、简单圈、 圈:v0 = vn 的链称为圈或闭链 初等圈:圈中所含的点均不相同 简单圈:圈中所含的边均不相同 连通图:图中任意两点之间均至少 有一条链,否则称作不连 通图。 连通分支: 支撑子图(生成子图): 如果 V2 = V1 , E2 E1 ,称 G2 是 G1 的 支撑子图(生成子图). 有向图相关概念 基础图:有向图中去掉所有弧上的箭头, 得到的无向图。 弧:有向图的边a=(u ,v),起点u,终点v; 路:若有从 u 到 v 不考虑方向的链,且 各方向一致,则称之为从u到v的路; 初等路: 各顶点都不相同的路; 初等回路:u = v 的初等路; 无向图中的概念总结 • 多重边 奇点 • 简单图 偶点 • 多重图 链 • 环 圈 • 次 初等(简单)链 • 悬挂点 初等(简单)圈 • 悬挂边 连通图 • 孤立点 支撑子图 v1 e1 e2 e3 e3 e4 e5 e6 v2 v3 v v4 v 5 6 无向图的性质 定理1 (握手定理)所有顶点次数之和等于所有边数 的2倍。 定理2 在任一图中,奇点的个数必为偶数。 以下各点能不能是某简单图的顶点的次的序列? (1)7,6,5,4,3,2 (2)6,6,5,4,3,2,1
6.2最小支撑树 [例们今有保气站A,将给一居民区供应煤气,居民区各用 本节主要内容: △ 树的性质 树的概念与性质 树:无圈连通图 (1)G为树: 例判断下面图形哪个是树 (2)G连通,且边数=点数.1 C温c命动后 (3)G无圈,且边数-点数1: (5)任意两个顶点之间恰有一条链。 △ 图的支撑树 定理3国G有支排树充要条件是图G是连通, (】南法 问题:如何找一个图的支掉树??? 在里搜接来步的雷串鞋包酱对途下的图 在该方法中,去掉的边戴为:边数点数+1 AN△ 4
4 6.2 最小支撑树 本节主要内容: 树及其 性质 图的 支撑树 最小支撑树 问题 [例]今有煤气站A,将给一居民区供应煤气,居民区各用 户所在位置如图所示,铺设各用户点的煤气管道所需的费 用(单位:万元)如图边上的数字所示。要求设计一个最 经济的煤气管道路线,并求所需的总费用。 3.5 A B C D E F G H I J K S 2 2 2 2 2 2 5 4 5 2 6 3 4 5 3 1 树: 无圈连通图 (A) (B) (C) 例 判断下面图形哪个是树: 一、 树的概念与性质 树的性质 设G=(V,E),V=(v1 ,v2 ,…vm),E= (e1 ,e2 ,…en),下列关于树的命题相互等 价: (1)G为树; (2)G连通,且边数=点数-1; (3)G无圈,且边数=点数-1; (4)G连通,且删去G中任一条边后不连 通; (5)任意两个顶点之间恰有一条链。 若一个图 G =(V , E)的支撑子图 T=(V , E´) 构 成树,则称 T 为G的支撑树,又称生成树、部分树。 图的支撑树 (G) (G1 ) (G2 ) (G3 ) (G4 ) 例 定理3 图G有支撑树充要条件是图G是连通。 (1)破圈法 在图中任取一个圈,从圈中去掉一边,对余下的图 重复这个步骤,直到图中不在包含圈为止。 在该方法中,去掉的边数为:边数-点数+1 A B C D A B C D A B C D A B C D 问题:如何找一个图的支撑树???
(2)避圈法 二、最小支撑树问题 方法中 取出 图的所有树中权最小的树称为最小支撑树 公人 5 4 4 △ △ 求最小支撑树一避国法 求最小支撑树一破国法 以后每一步中 不含圈的图为止。 A性 △世 有想A。将给一民区应气。居民区 1 此即为最经济的煤气管道路线,所需的总费用为25万元 A整丝 A性
5 (2)避圈法 由图的任一顶点开始,逐步生成该图的支撑树。 在该方法中,取出的边数为:点数-1 A B C D A B C D 二、最小支撑树问题 • 给图G=(V,E),对G中的每一条边[vi ,vj ],相应 地有一个数wij,则称这样的图G为赋权图,wij称 为边[vi ,vj ]上的权。 • 图的所有树中权最小的树称为最小支撑树。 A B C D F E 6 5 1 5 7 2 3 4 4 求最小支撑树—避圈法 在图中选一条最小权的边,以后每一步中,总从未 被选取的边中选一条权最小的边,并使之与已选取 的边不构成圈(每一步中,如果有两条或两条以上 的边都是权最小的边,则从中任取一条)。 A B C D F E 5 1 2 3 6 5 7 4 4 求最小支撑树—破圈法 在图中任取一个圈,从圈中去掉一条权最大的边(如果 有两条或两条以上的边都是权最大的边,则任意去掉其 中一条),在余下的图中,重复这一步骤直至得到一个 不含圈的图为止。 A B C D F E 6 5 1 5 7 2 3 4 4 [例]今有煤气站A,将给一居民区供应煤气,居民区各 用户所在位置如图所示,铺设各用户点的煤气管道所需 的费用(单位:万元)如图边上的数字所示。要求设计 一个最经济的煤气管道路线,并求所需的总费用。 3.5 A B C D E F G H I J K S 2 2 2 2 2 2 5 4 5 2 6 3 4 5 3 1 I J A B C D E F G H K S 2 2 2 2 2 2 2 3 4 3 1 此即为最经济的煤气管道路线,所需的总费用为25万元
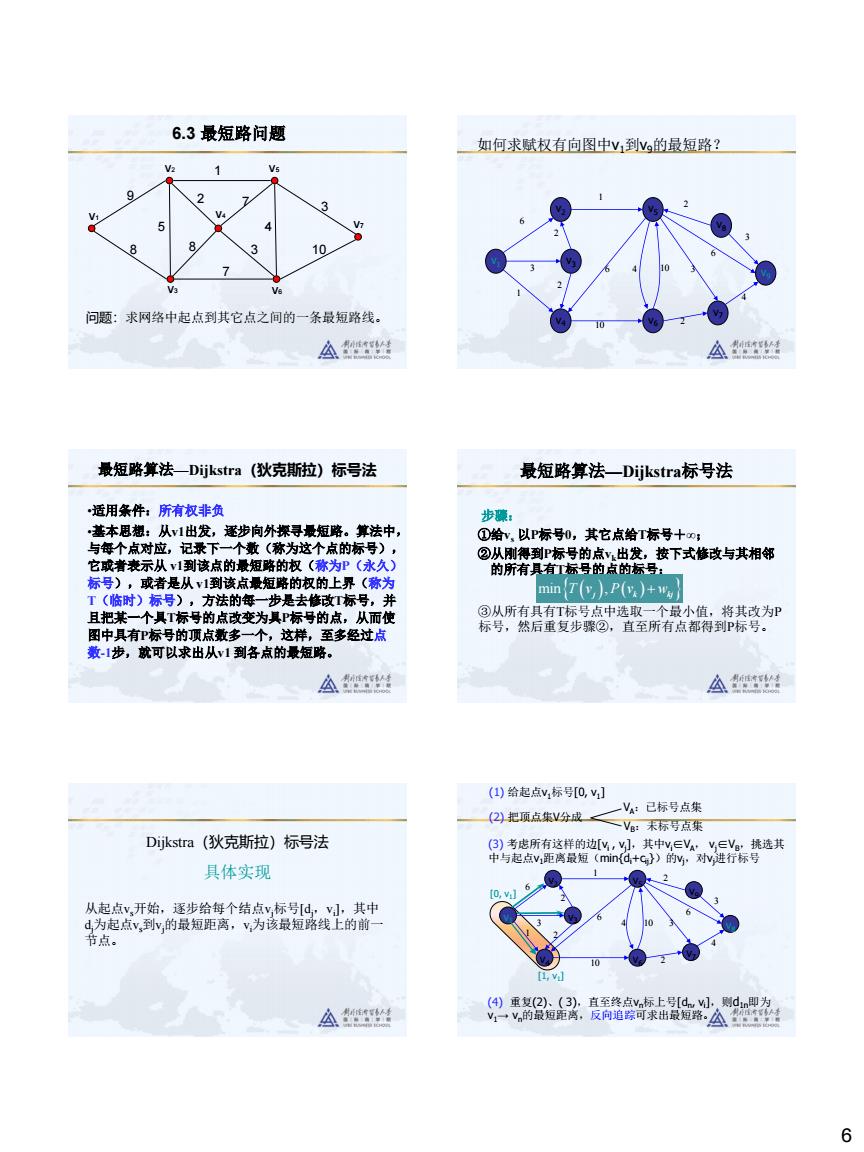
6.3最短路问题 如何求赋权有向图中y到v的最短路 1 问题:求网络中起点到其它点之间的一条最短路线。 A性 最短路算法一Dijkstra(狄克斯拉)标号法 最短路算法一Dijkstra标号法 适用条件:所有权非负 善本思想:从v1出发,逐步向外探寻最短路。算法中 与每个成对应,记承下 ②从刚得 min T(v).P(v)+w 且把某一个具T标号的点支变为具P标号的点,从而使 △ ()给起点v,标[0, V:已标号点集 (2把顶点集V分成二V末际与点集 Dijkstra(狄克斯拉)标号法 具体实现 A兰 歌金 6
6 6.3 最短路问题 v1 v2 v5 v3 v4 v6 v7 9 5 8 1 2 8 7 7 3 4 3 10 问题:求网络中起点到其它点之间的一条最短路线。 v2 v1 v3 v4 v5 v6 v7 v8 v9 1 6 3 2 2 2 2 6 6 1 3 3 10 4 10 4 如何求赋权有向图中v1到v9的最短路? 最短路算法—Dijkstra(狄克斯拉)标号法 •适用条件:所有权非负 •基本思想:从v1出发,逐步向外探寻最短路。算法中, 与每个点对应,记录下一个数(称为这个点的标号), 它或者表示从 v1到该点的最短路的权(称为P(永久) 标号),或者是从 v1到该点最短路的权的上界(称为 T(临时)标号),方法的每一步是去修改T标号,并 且把某一个具T标号的点改变为具P标号的点,从而使 图中具有P标号的顶点数多一个,这样,至多经过点 数-1步,就可以求出从v1 到各点的最短路。 最短路算法—Dijkstra标号法 步骤: ①给vs 以P标号0,其它点给T标号+∞; ②从刚得到P标号的点vk出发,按下式修改与其相邻 的所有具有T标号的点的标号; min , T v P v w ( j k kj ) ( ) + ③从所有具有T标号点中选取一个最小值,将其改为P 标号,然后重复步骤②,直至所有点都得到P标号。 Dijkstra(狄克斯拉)标号法 具体实现 从起点vs开始,逐步给每个结点vj标号[dj,vi ],其中 dj为起点vs到vj的最短距离,vi为该最短路线上的前一 节点。 [1, v1 ] [0, v1 ] (1) 给起点v1标号[0, v1 ] (3) 考虑所有这样的边[vi , vj ],其中vi∈VA, vj∈VB,挑选其 中与起点v1距离最短(min{di+cij})的vj,对vj进行标号 (4) 重复(2)、( 3),直至终点vn标上号[dn , vi ],则d1n即为 v1→ vn的最短距离,反向追踪可求出最短路。 (2) 把顶点集V分成 VA:已标号点集 VB:未标号点集 10 v2 v1 v3 v4 v5 v6 v7 v9 v8 1 6 3 2 2 2 2 6 6 1 3 4 10 3 4

反向追踪 魔的净 此时仅有T标号 尽丝 最短路问题一应用举例 最短路问题应用 一设备更新问题 第1年第2年第3年第4年第5年 高造装霜 1111121213 于析:结点:V=,V},表示 g智 [16,v 30,w] 59 [53,v/w 41 △兰 A丝性 6.4网络最大流问题 公路系统中的车钙流 供水系统中的水流 控制系统中的信息流 问题背景 金融系统中的现金流 A整 A丝 1
7 [0, v1 ] [1, v1 ] 此时仅有T标号的点为v9,T(v9 )=+∞,算法终止. v8已标号[12, v5 ],则12即为v1→ v8的最短距离,反向追踪 可求出最短路! [3, v1 ] [5, v3 ] [6, v2 ] [9, v5 [10, v5 ] ] [12, v5 ] 10 v2 v1 v3 v4 v5 v6 v7 v9 v8 1 6 3 2 2 2 2 6 6 1 3 4 10 3 4 [0, v1 ] [1, v1 ] [3, v1 ] [5, v3 ] [6, v2 ] [9, v5 [10, v5 ] ] [12, v5 ] v1到v8的最短路为:v1→ v3→ v2→ v5→ v8,最短距离为12 10 v2 v1 v3 v4 v5 v6 v7 v9 v8 1 6 3 2 2 2 2 6 6 1 3 4 10 3 4 反向追踪 最短路问题—应用举例 第1年 第2 年 第3 年 第4 年 第5年 11 11 12 12 13 使用年数 0-1 1-2 2-3 3-4 4-5 维修费用 5 6 8 11 18 16 16 17 17 18 22 30 41 59 22 30 41 23 31 23 v1 v2 v3 v4 v5 v6 最短路问题应用——设备更新问题 v2 v1 v3 v4 v5 v6 第i年 1 2 3 4 5 价格ai 11 11 12 12 13 使用寿命 0~1 1~2 2~3 3~4 4~5 费用bj 5 6 8 11 18 [0,v1 ] [16,v1 ] [22,v1 ] [30,v1 ] [41,v1 ] [53,v3 /v4 ] 16 分析:结点:V={v1,…,v6}, vi表示第i年初; 边: E={(vi,vj )} 表示第i年初购买,用至第j年初;i= 1,…,5; j= 2,…,6 权cij: i年初~ j年初的费用,即cij= i年初购买费+(j-i)年里的维修费 30 22 41 59 16 22 30 41 17 23 31 17 23 18 v2 v1 v3 v4 v5 v6 [0,v1 ] [16,v1 ] [22,v1 ] [30,v1 ] [41,v1 ] [53,v3 /v4 ] 16 30 22 41 59 16 22 30 41 17 23 31 17 23 18 公路系统中的车辆流 6.4 网络最大流问题 控制系统中的信息流 供水系统中的水流 金融系统中的现金流 问题背景

问题的提出 (一)基本概念 V。5 4 8 5 17 上指定义在集合上的一个备 男务文爱风是不二装盟大 ft.u 管2骑得的提条线路使得从起点 其中心)5叫做美,)上的流叠。 △ A图 53) 品 13(5 605 41) 42 对于收点,有三-山=" 对于中间点,有二-影=0 10 竖 图中(仍,)为零流弧,其余为非饱和弧 A性 容量网络G 为网络中从v到 5 定向 和 135 52 4 5 42 了是一个可行流,如果满足: 9 、4 10 则称为从,到,的关于的一条增广链。 大的充分条件是不存在从 4=,吗%,h,,}4=g,y} 显圈中增广连不止一条 A A性 8
8 问题的提出 • 网络中存在流量限制时,求解一条线路使得从起点 与终点之间可通过的流量最大。 v1 v2 v3 v4 v5 v6 10 8 4 6 5 3 5 3 11 17 例:上图为V1到V6的一交通网,权表示相应运输线的最大 通过能力,制定一方案,使从V1运到V6的产品数量最多。 (一) 基本概念 1、设一个赋权有向图D=(V, E),在V中指定一个发点vs 和一个收点vt ,其它的点叫做中间点。对于D中的每一个弧 (vi , vj)∈E ,都有一个非负数cij,叫做弧的容量。我们把这 样的图D叫做一个容量网络,简称网络,记做 D=(V,E,C)。 网络D上的流,是指定义在弧集合E上的一个函数 其中f(vi ,vj ) =fij 叫做弧(vi,vj )上的流量。 ( , ) { } i j i j f = f v v = f 2、称满足下列条件的流为可行流: (1)容量条件:对于每一个弧(vi ,vj)∈E,有 0 ≤ f ij ≤ cij 。 (2)平衡条件: 对于发点vs,有 对于收点vt ,有 对于中间点,有 − = v v E v v E s j js s j j s f f W ( , ) ( , ) − = − v v E v v E t j jt t j j t f f W ( , ) ( , ) − = v v E v v E i j j i i j j i f f ( , ) ( , ) 0 可行流中 f ij=cij 的弧叫做饱和弧,f ij<cij的弧叫做非 饱和弧。f ij>0 的弧为非零流弧,f ij=0 的弧叫做零流 弧。 2 v 1 v 3 v 4 v 5 v 6 v 7 v 13 (5) 9 (3) 4 (1) 5 (3) 6(3) 5 (2) 5 (2) 5 (0) 4 (2) 4 (1) 9 (5) 10 (1) 图中 (v3 , v6 ) 为零流弧,其余为非饱和弧。 3、容量网络G,若 为网络中从vs到vt的一条链,给 定向为从vs到vt, 上的弧凡与 方向相同的称为前向弧, 凡与 方向相反的称为后向弧,其集合分别用 和 表 示。 f 是一个可行流,如果满足: 则称 为从vs到vt 的关于f 的一条增广链。 + − − + 0 ( , ) 0 ( , ) i j i j i j i j i j i j f c v v f c v v 推论 可行流f 是最大流的充分必要条件是不存在从vs到vt 的关于f 的一条可增广链。 即 中的每一条弧都是非饱和弧 + 即 中的每一条弧都是非零流弧 − 2 v 1 v 3 v 4 v 5 v 6 v 7 v 13 (5) 9 (3) 4 (1) 5 (3) 6(3) 5 (2) 5 (2) 5 (0) 4 (2) 4 (1) 9 (5) 10 (1) = v1 ,(v1 ,v2 ),v2 ,(v3 ,v2 ),v3 ,(v3 ,v6 ),v6 ,(v6 ,v7 ),v7 = (v1 ,v2 ),(v3 ,v6 ),(v6 ,v7 ) + = (v3 ,v2 ) − 是一条增广链 显然图中增广链不止一条

((二)求最大流的标号法 调整过程 )如果边)eE,且>0,那么给标号 f+6m.v)en 边无中E置郑么给标号 (V..v) 3 下发过程无法进行 号子去菊所有标号,风到第一东,对可行瓷童新 这时的可行流就是最大流。 A图 A华四 6.5最小费用最大流问题 6.5最小费用最大流问题 在麦厅性樂爱使考唐消整朵到有关婆的贸考的 整r雀出药 若:是从,到,的增广链中费用最小的增广链,则称口是最 点中的费用是 最小费用最大流问愿成是要解决这一类愿, △世 A丝性 步骤: 2当)为径老网警骋8少)的反向道,令 整量为 -当,0 8=mm6,-,( 事粱歌C景药泰品小费用增广鞋等价于你门中 A A丝 9
9 (二) 求最大流的标号法 标号过程: 1. 给发点vs 标号(0,+∞)。 2. 取一个已标号的点vi,对于vi一切未标号的邻接点 vj 按下列规则处理: (1)如果边 ,且 ,那么给vj 标号 ,其中: (2)如果边 ,且 ,那么给vj 标号 ,其中: 3.重复步骤2,直到vt被标号或标号过程无法进行下 去,则标号结束。若vt被标号,则存在一条增广链,转 调整过程;若vt未被标号,而标号过程无法进行下去, 这时的可行流就是最大流。 (v j ,vi) E f j i 0 ( , ) i j −v min( , ) j ji i = f (vi ,v j ) E ij ij f c ( , ) i j +v min( , ) j i j i j i = c − f 调整过程 设 1.令 2.去掉所有标号,回到第一步,对可行流重新标 号。 min{ ( , ) } 1 + = ci j − f i j vi v j min{ ( , ) } 2 − = f i j vi v j min( , ) = 1 2 − + = − + ( , ) ( , ) ( , ) i j i j i j i j i j i j i j f v v f v v f v v f 在实际的网络系统中,当涉及到有关流的问题的 时候,我们往往不仅仅考虑的是流量,还经常要考虑 费用的问题。 例如一个铁路系统的运输网络流,既要考虑网络 流的货运量最大,又要考虑总费用最小。 最小费用最大流问题就是要解决这一类问题。 6.5 最小费用最大流问题 6.5 最小费用最大流问题 定义 已知网络G =(V,E,C,d),f是G上的一个可行流, 为一条从vs到v t的增广链, = + −− 称为链的费用。 di j di j d( f ) 若 * 是从vs到vt的增广链中费用最小的增广链,则称 * 是最 小费用增广链。 结论:如果可行流 f在流量为W(f )的所有可行流中的费用最 小,并且 *是关于f 的所有增广链中的费用最小的增广链, 那么沿增广链 *调整可行流f,得到的新可行流f *也是流量 为W(f * )的所有可行流中的最小费用流。当f * 是最大流时,就 是最小费用最大流。 寻找关于f 的最小费用增广链: 构造一个关于f 的赋权有向图L(f ) ,其顶点是原网 络G的顶点,而将G中的每一条弧 ( vi , vj )变成两个相反 方向的弧(vi, vj)和(vj , vi ),并且定义图中弧的权l ij为 : 1.当 ,令 2.当(vj,vi)为原来网络G中(vi, vj)的反向弧,令 在网络G中寻找关于f 的最小费用增广链等价于在L(f )中 寻求从vs 到vt 的最短路。 + = = i j i j i j i j i j i j f c d f c l 当 当 + = − = 0 0 i j i j i j ji f d f l 当 当 (vi , v j) E 步骤: (1)取零流为初始可行流 ,f (0) ={0}。 (2)一般地,如果在第k-1步得到最小费用流 f (k-1),则 构造图 L( f (k-1) )。 (3)在L( f (k-1) )中,寻求从vs到vt的最短路。若不存在最 短路,则f (k-1)就是最小费用最大流;否则转(4)。 (4)如果存在最短路,则在可行流f (k-1)的图中得到与此 最短路相对应的增广链,在增广链上,对f (k-1)进行调整 ,调整量为: = − − − − + min min ( ) , min ( ) ( 1) (k 1) i j k i j i j c f f
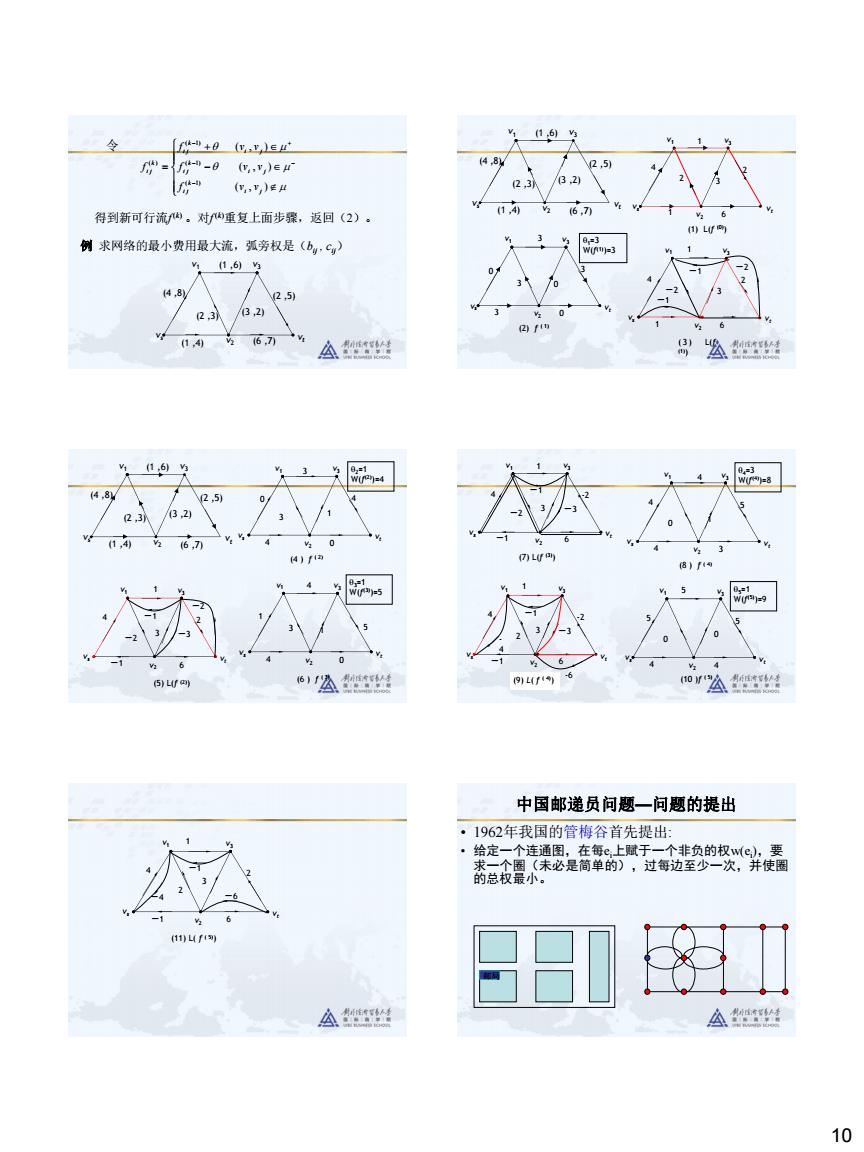
(te (E 瑞={--0%)eμ )层4 得到新可行流内。对四重复上面步骤,返回(2)。 例求网路的最小费用最大流,弧旁权是(6,C,) %16) 23认/2 中国邮递员问惠一问题的提出 1962年我国的管梅谷首先提出 o
10 − + = − − − − + ( , ) ( , ) ( , ) ( 1) ( 1) ( 1) ( ) i j k i j i j k i j i j k i j k i j f v v f v v f v v f 令 得到新可行流f (k) 。对f (k)重复上面步骤,返回(2)。 例 求网络的最小费用最大流,弧旁权是(bij , cij) (3 ,2) vs v2 v1 vt v3 (1 ,4) (6 ,7) (4 ,8) (1 ,6) (2 ,5) (2 ,3) 3 vs v2 v1 vt v3 1 6 4 1 2 2 (1) L(f (0) ) (3 ,2) vs v2 v1 vt v3 (1 ,4) (6 ,7) (4 ,8) (1 ,6) (2 ,5) (2 ,3) 0 vs v2 v1 vt v3 3 0 0 3 3 3 (2) f ( 1) 1=3 W(f (1) )=3 -1 ( 3 ) L(f (1) ) -2 3 vs v2 v1 vt v3 1 6 4 1 2 -1 -2 1 vs v2 v1 vt v3 4 0 0 3 4 3 (4 ) f ( 2) 2=1 W(f (2) )=4 (3 ,2) vs v2 v1 vt v3 (1 ,4) (6 ,7) (4 ,8) (1 ,6) (2 ,5) (2 ,3) (5) L(f (2) ) -3 vs v2 v1 vt v3 -1 4 1 2 -2 -2 3 -1 6 1 vs v2 v1 vt v3 4 0 1 4 3 5 (6 ) f ( 3) 3=1 W(f (3) )=5 (7) L(f (3) ) vs v2 v1 vt v3 -3 -1 4 1 -2 -2 3 -1 6 1 vs v2 v1 vt v3 4 3 4 4 5 0 (8 ) f ( 4) 4=3 W(f (4) )=8 0 vs v2 v1 vt v3 4 4 5 5 5 0 5=1 W(f (5) )=9 (10 )f ( 5) -1 -2 3 -1 vs v2 v1 vt v3 -3 4 1 2 6 (9) L( f ( 4) ) - 4 -6 3 -1 2 -1 4 (11) L( f ( 5) ) 1 2 6 -4 vs v2 v1 vt v3 -6 中国邮递员问题—问题的提出 • 1962年我国的管梅谷首先提出: • 给定一个连通图,在每ei上赋于一个非负的权w(ei ),要 求一个圈(未必是简单的),过每边至少一次,并使圈 的总权最小。 邮局