
2019/6/20 本章内容 第5章动态规划 5.1动态规划简介 Dynamic Programming 5.2动态规划的本思想 5.3离散确定性问题的动态规划解法 马像 5.4一般数学规划横型的动态规划解法 国际商学院 2019年6月3日 △ 5.1动态规划简介 动态决策问趣的特点: 动态规划是用来解决多阶段决策过程最优化的 所处的状态,不断地做出决策: 找到不同时刻的最优决策以及整个过程的最优策略。 地去解决。 多阶段决策问题: 种方 是动态决策问题的一种特殊形式: ,而不是 中算法 速立相应的横型,然后再用动态规划方法去求 终来整 您钠宽紧选行决完目的是使个过遥的决策 △ 我链楼连装毒速 黄餐者格余 完好的花 为a40水1 多阶段决策问题的典型例子: 的在丹芙氯头产品的年产量啸投入生护产 企业在生 h=h() 年和需求共定生计 相应的机暑年完好率A0<K1。 假定开牛产时完好的机是表为:要求制 粉帆4药 下生产的最 △兰
2019/6/20 1 第5章 动态规划 Dynamic Programming 马俊 国际商学院 2019年6月3日 1 5.1 动态规划简介 5.2 动态规划的基本思想 5.3 离散确定性问题的动态规划解法 5.4 一般数学规划模型的动态规划解法 本章内容 2 动态规划是用来解决多阶段决策过程最优化的 一种数量方法。其特点在于,它可以把一个n 维决 策问题变换为几个一维最优化问题,从而一个一个 地去解决。 需指出:动态规划是求解某类问题的一种方法, 是考察问题的一种途径,而不是一种算法。必须对 具体问题进行具体分析,运用动态规划的原理和方 法,建立相应的模型,然后再用动态规划方法去求 解。 5.1 动态规划简介 3 即在系统发展的不同时刻(或阶段)根据系统 所处的状态,不断地做出决策; 每个阶段都要进行决策,目的是使整个过程的决策 达到最优效果。 动态决策问题的特点: 系统所处的状态和时刻是进行决策的重要因素; 找到不同时刻的最优决策以及整个过程的最优策略。 多阶段决策问题: 是动态决策问题的一种特殊形式; 在多阶段决策过程中,系统的动态过程可以按照时间 进程分为状态相互联系而又相互区别的各个阶段; 4 多阶段决策问题的典型例子: 1 . 生产决策问题:企业在生产过程中,由于需 求是随时间变化的,因此企业为了获得全年的最佳 生产效益,就要在整个生产过程中逐月或逐季度地 根据库存和需求决定生产计划。 2. 机器负荷分配问题:某种机器可以在高低两 种不同的负荷下进行生产。在高负荷下进行生产时, 产品的年产量g和投入生产的机器数量u1的关系为 g=g(u1) 1 2 n 状态 决策 状态 决策 状态 状态 决策 5 这时,机器的年完好率为a,即如果年初完好机 器的数量为u,到年终完好的机器就为au, 0<a<1。 在低负荷下生产时,产品的年产量h和投入生产 的机器数量u2的关系为 h =h(u2) 假定开始生产时完好的机器数量为s1。要求制 定一个五年计划,在每年开始时,决定如何重新 分配完好的机器在两种不同的负荷下生产的数量, 使在五年内产品的总产量达到最高。 相应的机器年完好率b, 0< b<1。 6
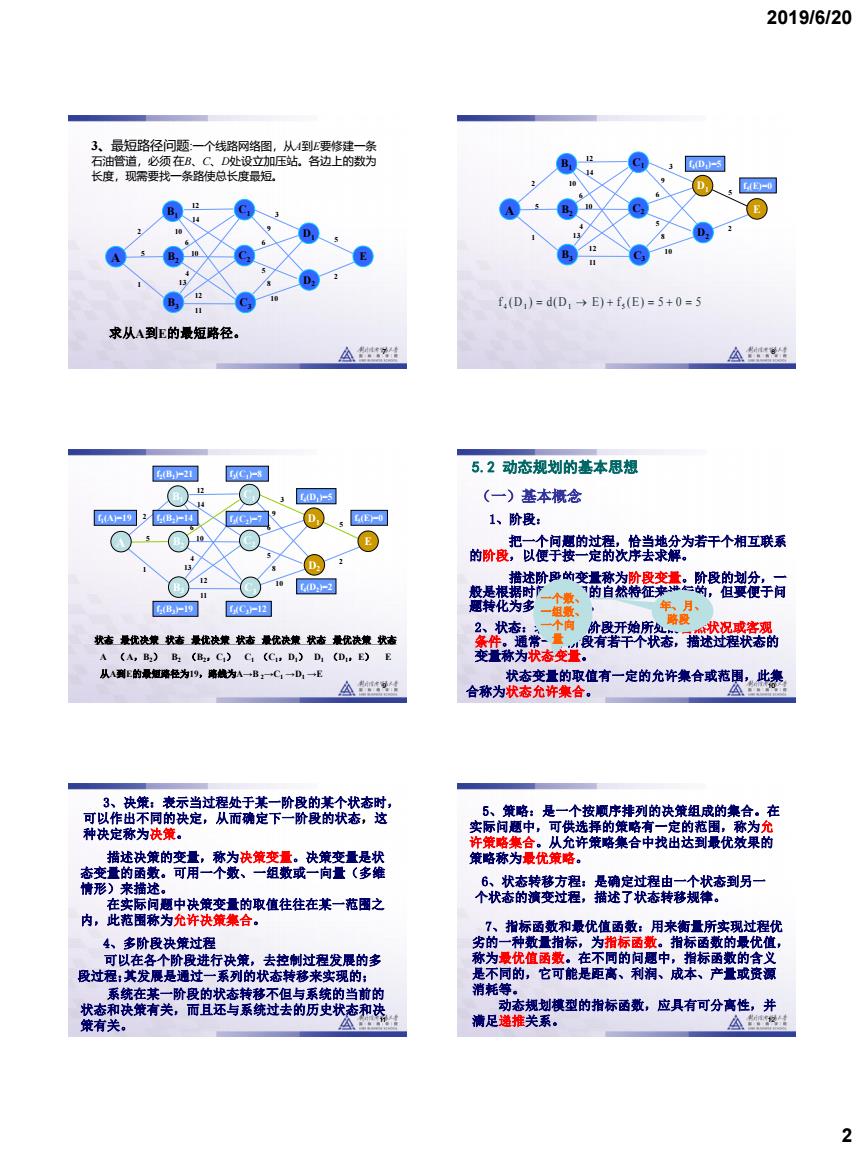
2019/6/20 玉最短路 长度,现需要找一条路使总长度最短。 fE-0 B f(D,)=d(D,→E)+,(E)=5+0=5 求从A到E的最短路径, A出 △t相 5.2动态规划的基本思想 (一)基本概念 1、阶段: 的阶或把以樱的茫器棉美装为者干个相互联系 L(D:F-2 B可e的 表特石 状志量优决檬状春量优决泉状志量优决巢状志量优决我洁 食,的 △出 合光袋著表精程值有一定的光许集合孩明,特 可以作集斋须是凝阶跳的麟歌装声这 排列的决策组 的舞 种决定称为决策。 许略集合中找出达到豪优的 庄实际同愿中决策变量的取值往往在某一落围之 内,此范雷称为允许决策集合。 指标函数和最优值通数:用来衡量所实现过 4、多阶段决策过程 数量指标 为 指 的景优值 消耗等 规划模型的指标函数,应具有可分离性, 清足推关系
2019/6/20 2 2 5 1 12 14 10 6 10 4 13 11 12 3 9 6 5 8 10 5 2 C1 C3 D1 A B1 B3 B2 D2 C2 E 3、最短路径问题:一个线路网络图,从A到E要修建一条 石油管道,必须 在B、C、D处设立加压站。各边上的数为 长度,现需要找一条路使总长度最短。 求从A到E的最短路径。 7 2 5 1 12 14 10 6 10 4 13 11 12 3 9 6 5 8 10 5 2 C1 C3 D1 A B1 B3 B2 D2 C2 E f4 (D1 )=5 f5 (E)=0 f (D ) d(D E) f (E) 5 0 5 4 1 = 1 → + 5 = + = 8 2 5 1 12 14 10 6 10 4 13 11 12 3 9 6 5 8 10 5 2 C1 C3 D1 A B1 B3 B2 D2 C2 E f4 (D2 )=2 f5 (E)=0 f3 (C3 )=12 f4 (D1 )=5 f2 (B3 )=19 f3 (C2 )=7 f3 (C1 )=8 f1 (A)=19 f2 (B2 )=14 f2 (B1 )=21 状态 最优决策 状态 最优决策 状态 最优决策 状态 最优决策 状态 A ( A,B2) B2 (B2,C1) C1 (C1,D1) D1 (D1,E) E 从A到E的最短路径为19,路线为A→B 2→C1 →D1 →E 9 (一)基本概念 1、阶段: 把一个问题的过程,恰当地分为若干个相互联系 的阶段,以便于按一定的次序去求解。 描述阶段的变量称为阶段变量。阶段的划分,一 般是根据时间和空间的自然特征来进行的,但要便于问 题转化为多阶段决策。 2、状态:表示每个阶段开始所处的自然状况或客观 条件。通常一个阶段有若干个状态,描述过程状态的 变量称为状态变量。 年、月、 路段 一个数、 一组数、 一个向 量 状态变量的取值有一定的允许集合或范围,此集 合称为状态允许集合。 5.2 动态规划的基本思想 10 3、决策:表示当过程处于某一阶段的某个状态时, 可以作出不同的决定,从而确定下一阶段的状态,这 种决定称为决策。 描述决策的变量,称为决策变量。决策变量是状 态变量的函数。可用一个数、一组数或一向量(多维 情形)来描述。 在实际问题中决策变量的取值往往在某一范围之 内,此范围称为允许决策集合。 系统在某一阶段的状态转移不但与系统的当前的 状态和决策有关,而且还与系统过去的历史状态和决 策有关。 4、多阶段决策过程 可以在各个阶段进行决策,去控制过程发展的多 段过程;其发展是通过一系列的状态转移来实现的; 11 5、策略:是一个按顺序排列的决策组成的集合。在 实际问题中,可供选择的策略有一定的范围,称为允 许策略集合。从允许策略集合中找出达到最优效果的 策略称为最优策略。 6、状态转移方程:是确定过程由一个状态到另一 个状态的演变过程,描述了状态转移规律。 7、指标函数和最优值函数:用来衡量所实现过程优 劣的一种数量指标,为指标函数。指标函数的最优值, 称为最优值函数。在不同的问题中,指标函数的含义 是不同的,它可能是距离、利润、成本、产量或资源 消耗等。 动态规划模型的指标函数,应具有可分离性,并 满足递推关系。 12

2019/6/20 动本制方法是 (二)动态规划的基本思想 2、在多阶段决策过程中, 当的 段和未米一段分开 未来教 1、动态规划方法的关链在于正确地写出基本的递 选取是从全局来考的,与该段的豪优选择案一般 关系式和 是不同的年求个同愿的最优策略时, 由于初始状本 阶当的选取状 决策变量及定义最优值 段的 快镜是该 松后逐个求解。即从边界条件开始,逐段递推寻优, 定了最路线。 最 个过程的最优策略具有这 代子染成的也是说;比的 (三)建立动态规划模型的步摄 动态规划的基本方程 1、划分阶段 分阶受是 逆序解法 多阶 =4(月=- 2、正确选择状态变量 5.=0 餐 3、确定决策变量及允许决策集合 叶模空绿袋者格精楚癸染】 4、确定状态转移方程 5.3 志变整量软熟松芳被先著鑫关景1阶慢状 刘金阶段指标西最来和最优指标高最,意立动态凝 下表所示。 题0102030405060 2是程 gx020506508585 20204050556065 黄 解:依据题意,是要求£(6
2019/6/20 3 1、动态规划方法的关键在于正确地写出基本的递 推关系式和恰当的边界条件(简称基本方程)。要做 到这一点,就必须将问题的过程分成几个相互联系的 阶段,恰当的选取状态变量和决策变量及定义最优值 函数,从而把一个大问题转化成一组同类型的子问题, 然后逐个求解。即从边界条件开始,逐段递推寻优, 在每一个子问题的求解中,均利用了它前面的子问题 的最优化结果,依次进行,最后一个子问题所得的最 优解,就是整个问题的最优解。 (二)动态规划的基本思想 13 2、在多阶段决策过程中,动态规划方法是既把 当前一段和未来一段分开,又把当前效益和未来效益 结合起来考虑的一种最优化方法。因此,每段决策的 选取是从全局来考虑的,与该段的最优选择答案一般 是不同的. 最优化原理:作为整个过程的最优策略具有这样 的性质:无论过去的状态和决策如何,相对于前面的 决策所形成的状态而言,余下的决策序列必然构成最 优子策略。”也就是说,一个最优策略的子策略也是 最优的。 3、在求整个问题的最优策略时,由于初始状态 是已知的,而每段的决策都是该段状态的函数,故最 优策略所经过的各段状态便可逐段变换得到,从而确 定了最优路线。 14 动态规划的基本方程 逆序解法: ( ) ( ) ( , , 1,...,1 ) 1 1 ( ) k k k k k k k k k k u D s f s opt v s u f s k n n + + = + = − 1 1 ( ) 0 n n f s + + = 顺序解法: ( ) ( ) ( ) ( ) 1 1 1 1 , 1,2,..., r k k k k k k k k k k u D s f s opt v s u f s k n + + + − = + = f s 0 1 ( ) = 0 15 (三)建立动态规划模型的步骤 1、划分阶段 划分阶段是运用动态规划求解多阶段决策问题的第 一步,在确定多阶段特性后,按时间或空间先后顺序, 将过程划分为若干相互联系的阶段。对于静态问题要人 为地赋予“时间”概念,以便划分阶段。 2、正确选择状态变量 选择变量既要能确切描述过程演变又要满足无后效 性,而且各阶段状态变量的取值能够确定。一般地,状 态变量的选择是从过程演变的特点中寻找。 3、确定决策变量及允许决策集合 通常选择所求解问题的关键变量作为决策变量,同 时要给出决策变量的取值范围,即确定允许决策集合16。 4、确定状态转移方程 根据k 阶段状态变量和决策变量,写出k+1阶段状 态变量,状态转移方程应当具有递推关系。 5、确定阶段指标函数和最优指标函数,建立动态规 划基本方程 阶段指标函数是指第k 阶段的收益,最优指标函 数是指从第k 阶段状态出发到第n 阶段末所获得收益 的最优值,最后写出动态规划基本方程。 以上五步是建立动态规划数学模型的一般步骤。 由于动态规划模型与线性规划模型不同,动态规划模 型没有统一的模式,建模时必须根据具体问题具体分 析,只有通过不断实践总结,才能较好掌握建模方法 与技巧。 17 5.3 离散确定性动态规划模型的求解 例:设国家拨给60万元投资,供四个工厂扩建使 用,每个工厂扩建后的利润与投资额的大小有关,投 资后的利润函数如下表所示。 投资 利润 0 10 20 30 40 50 60 g1 (x) 0 20 50 65 80 85 85 g2 (x) 0 20 40 50 55 60 65 g3 (x) 0 25 60 85 100 110 115 g4 (x) 0 25 40 50 60 65 70 解:依据题意,是要求 f4(60) 。 18

2019/6/20 装责餐法装。县按有伯一因,得到下表 82(0)+(60) 0+85 题·”000”0 9,(10)+f(50) 20+85 8(20)+(40 40+80 /=网02505055 &(30)+(30 ma 50+65 120 最优略0102030405060 g、40)+f20) 55+50 是局雅器餐设三个工 8(50)+f0) 60+20 &(60)+f(0) 65+0 5(60)=,max{&:)+(60-y》 最优策略为(40,20),此时最大利为120万元, 同理可求得其它£()的值。 A如 △出 投资0102030405060 [80)+2(60) 0+120) g,(10)+f(50) 25+105 020507090105120 (20)+/(40 60+90 ma 8,(30)+5(30 m 85+70 =155 g:(40)+f3(20 100+50 第县分生时香大的及第三 g:(50)+2(10) 110+20 g,(60)+f(0) 115+0 f万(60)=,ax{&()+f(60-y)} 最优策略为(20,10,30),最大利润为15万元。 △出 同理可求得头它,因的值.得到下表么堂型 [g:(0)+∫3(60) [0+155 5.4一般数学规划模型的动态规划解法 8.00)+万(50 25+135 8(20)+5(40 40+110 这里所说的一般数学规划模型包括线性 =axg,(30)+f(30) =max 50+85 =160 g(40)+(20) 规进 60+60 g,(50)+510) 65+25 要多阶段的决策过程 70+0 因而模型中含有多少个变量,求解就分成多 8:(60)+f(0) 少个阶段。约束条件的右端项表明可分配的 资源数,用状态变量表示。 最优策略为(20,0,30,10),最大利润为160万元。 △如学出 △坐 4
2019/6/20 4 按顺序解法计算。 第一阶段:求 f1(x)。显然有 f1(x) = g1(x),得到下表 投资 利润 0 10 20 30 40 50 60 f1 (x) = g1 (x) 0 20 50 65 80 85 85 最优策略 0 10 20 30 40 50 60 第二阶段:求 f2(x)。此时需考虑第一、第二个工厂 如何进行投资分配,以取得最大的总利润。 (60) max 2 ( ) 1 (60 ) 0,10, ,60 f 2 g y f y y = + − = 19 120 65 0 60 20 55 50 50 65 40 80 20 85 0 85 max (60) (0) (50) (10) (40) (20) (30) (30) (20) (40) (10) (50) (0) (60) max 2 1 2 1 2 1 2 1 2 1 2 1 2 1 = + + + + + + + = + + + + + + + = g f g f g f g f g f g f g f 最优策略为(40,20),此时最大利润为120万元。 同理可求得其它 f2(x) 的值。 20 投资 利润 0 10 20 30 40 50 60 f2 (x) 0 20 50 70 90 105 120 最优策略 (0,0) (10,0) (0,10) (20,0) (20,10) (20,20) (30,20) (40,20) 第三阶段:求 f3(x)。此时需考虑第一、第二及第三 个工厂如何进行投资分配,以取得最大的总利润。 (60) max 3 ( ) 2 (60 ) 0,10, ,60 f 3 g y f y y = + − = 21 155 115 0 110 20 100 50 85 70 60 90 25 105 0 120 max (60) (0) (50) (10) (40) (20) (30) (30) (20) (40) (10) (50) (0) (60) max 3 2 3 2 3 2 3 2 3 2 3 2 3 2 = + + + + + + + = + + + + + + + = g f g f g f g f g f g f g f 最优策略为(20,10,30),最大利润为155万元。 同理可求得其它 f3(x) 的值。得到下表 22 160 70 0 65 25 60 60 50 85 40 110 25 135 0 155 max (60) (0) (50) (10) (40) (20) (30) (30) (20) (40) (10) (50) (0) (60) max 4 3 4 3 4 3 4 3 4 3 4 3 4 3 = + + + + + + + = + + + + + + + = g f g f g f g f g f g f g f 最优策略为(20,0,30,10),最大利润为160万元。 23 5.4 一般数学规划模型的动态规划解法 这里所说的一般数学规划模型包括线性 规划、非线性规划、整数规划等,利用动态 规划进行求解时,主要思想是把依次决定各 个变量的取值看成是一个多阶段的决策过程, 因而模型中含有多少个变量,求解就分成多 少个阶段。约束条件的右端项表明可分配的 资源数,用状态变量表示。 24

2019/6/20 例:背包问愿 盘密为了孙物品的装件表(串负盛取)则间愿的教¥模 有一个使步擦行者,其可携带物品置量的限度为:公斤, 设有n种 mz-交 几件),使所起作用'(使用价值)大2 物品 月 ,之且为整兼0=12… 重量公斤/件) 4 用动态规方法求解。◆ 每件使用价值G,, C. 中禁档级紧 时的大还超过了公斤,包中只装有上物品 其中y≥0,k=1,名,口所以愿就是求£ 其递推关系式为: 例:求下面整囊规划问愿的最优解 f)=+fi-少-乃 max Z=8x+5x:+12x, 其中2≤k≤n 3x,+2x,+5x,≤5 ,x,5≥0且为整数 当k1时,有: w=)[s- 解:a=5,问愿是求f(6) (5)=mmx{12x+2(5-5x3)} 共二表示不短过的最大整数 =m0+5.2+上o 厂5=e,=3x2=3任,=1 5+5-2 LB)e6x.sSxs (.1 =5+5-2,} )=c,=8¥二=0国=0 5)
2019/6/20 5 有一个徒步旅行者,其可携带物品重量的限度为a 公斤, 设有n 种物品可供他选择装入包中。已知每种物品的重量 及使用价值(作用),问此人应如何选择携带的物品(各 几件),使所起作用(使用价值)最大? 物品 1 2 … j … n 重量(公斤/件) a1 a2 … aj … an 每件使用价值 c1 c2 … cj … cn 这就是背包问题。类似的还有工厂里的下料问题、运 输中的货物装载问题、人造卫星内的物品装载问题等。 例:背包问题 25 设xj 为第j 种物品的装件数(非负整数)则问题的数学模 型如下: = = = = 0 ( 1.2. . ) max 1 x j n a x a Z c x j n j i j j n j j j 且为整数 用动态规划方法求解,令 fk(y) = 总重量不超过 y 公斤,包中只装有前k 种物品 时的最大使用价值。 其中y ≥0, k =1,2, …, n 。所以问题就是求 fn(a) 26 其递推关系式为: k n f y ck xk f k y ak xk a y x k k k = + − − 2 ( ) max ( ) 1 0 其中 当 k=1 时,有: 其中 表示不超过 的最大整数 1 1 1 1 1 1 1 ( ) , a y a y a y x a y f y c = = 27 例:求下面整数规划问题的最优解 + + = + + , , 0且为整数 3 2 5 5 max 8 5 12 1 2 3 1 2 3 1 2 3 x x x x x x Z x x x 解:a=5 ,问题是求 f3(5) (5) max 12 (5 5 ) 3 2 3 5 0 3 3 3 3 f x f x x a x = + − 整 数 28 + + + − + − = + − = = ( 0) ( 1) 2 2 3 2 3 0 1 3 2 3 5 5 0 3 2 3 5 0 3 3 3 3 3 3 3 3 3 max 0 (5), 12 (0) max 12 (5 5 ) max 12 (5 5 ) (5) max 12 (5 5 ) x x x x x x a x f f x f x x f x f x f x = = = = , 整 数 整 数 29 + + + + − + − = + − = = = 5 5 ( 0) ( 1) ( 2) 1 1 1 2 1 2 0 1,2 2 1 2 2 5 0 2 1 2 5 0 2 2 2 2 2 2 2 2 2 2 max 0 (5), 5 (3), 10 (1) max (5 2 ) max (5 2 ) (5) max 5 (5 2 ) x x x x x x x a x f f f x f x x f x f x f x = = = = , 整 数 整 数 max 0 (0) (0) max (0 2 ) max (0 2 ) (0) max 5 (0 2 ) 1 ( 0) 1 2 1 2 0 2 1 2 2 0 0 2 1 2 0 0 2 2 2 2 2 2 2 2 f f x f x x f x f x f x x x x x x a x = + + − + − = + − = 5 5 = = = = 整 数 整 数 30 0 ( 0) 3 0 (0) 8 0 ( 0) 3 1 (1) 8 8 ( 1) 3 3 (3) 8 8 ( 1) 3 5 (5) 8 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 = = = = = = = = = = = = = = = = f c x x f c x x f c x x f c x x

2019/6/20 逆推解法 =mx65+810小=3(k=lx= x+x+x=c (C> 201=1,2,3 ÷55max0+55.12+5o) =mmx{0+13, 12+0} 雪面空面图同 所以,最优解为X=(1,1,0),最优值为Z=13。 6周6广圆=☒ △ △出 6
2019/6/20 6 (0) max 0 (0) (0) 0 ( 0, 0) 1 1 2 ( 0) 2 1 2 = = = = + = f f f x x x = 13 ( 1, 1, 0) max 0 13, 12 0 (5) max 0 (5), 12 (0) 1 2 3 ( 0) ( 1) 3 2 2 3 3 = = = = = + + + + = = x x x f f f x x = 所以,最优解为 X=(1, 1, 0),最优值为 Z = 13。 31 max8, 5 8, 10 13 ( 1, 1) (5) max 0 (5), 5 (3), 10 (1) 1 2 ( 0) ( 1) 2 2 1 1 1 2 2 2 = + = = = = + + + = = = x x f f f f x x x ( ) 逆推解法 2 2 1 3 1 2 3 max ( 0) 0 1,2,3 i z x x x x x x c c x i = + + = = 阶段1 阶段2 阶段3 1s c = 1 x 2 1 s c x = − 2 x 3 2 2 s s x = − 3 x 4 3 3 s s x = − ( ) ( ) f s s 3 3 3 ( ) = 2 2 2 2 3 3 f s x f s 1 1 1 2 2 ( ) = ( ) f s x f s = 32