西北大学化工原理电子教案 9.液体精馏 上一章我们讨论了气体吸收,即利用组分在液体溶剂中的溶解度不同来分离气体混合物 的方法。这一章我们讨论互溶液体混合物的常用分离方法或说典型单元操作,液体蒸馏即精 馏。 9.1蒸馏概述 蒸馏分离的依据对混合物的分离方法总是利用其中各组分某种性质的差异,而用蒸馏分离 混合物的依据或说其原理是:虽然各液体组分都能挥发,但各组分挥发程度不同,有难有易, 于是在部分汽化时,气相中所含易挥发组分将比液相中的多,使原来的混合液达到某种程度 的分离。同理,当混合气部分冷凝时,冷凝液中所含的难挥发组分将比气相中的多,也能达 到一定程度的分离。当然,利用一次部分汽化和部分冷凝的分离是不充分的,但是可以利用 这一原理进行反复分离,达到要求的纯度。显然,在部分汽化和部分冷凝时,气液两相的组 成差别愈大,将愈有利于蒸馏分离。而气液两相共存时最终组成的关系属于相平衡问题。 总的说来,蒸馏是分离互溶液体混合物的操作,其依据是液相中组分的挥发度不同,所 进行的过程是部分汽化部分冷凝,两相共存的组成分配关系受相平衡制约。 习惯上,把混合物中易挥发的组分称为轻组分,难挥发的组分称为重组分。 工业蒸馏过程 P608日0表0作花难 t●B0网0 然碳产品轻组分浓度较高 建非么简 塔:产品重组分浓度较高 ①按照操作方式分为间歇式和连续蒸馏: ②按蒸馏方法分为简单蒸馏,平衡蒸馏(闪馏),精馏和特殊精馏等: ③按操作压降分为常压、加压和减压精馏。比如在常压下为气态混合物,则可采用加压精馏: 沸点较高且为热敏性的物系可采用减压精馏。 按待分离物系中组分的数目可分为双(二元)组分和多组分精馏。工业中的精馏以多组 分精馏为主,但基本原理和计算与二元精馏无本质区别,所以本章着重讨论双组分常压精馏
西北大学化工原理电子教案 9. 液体精馏 上一章我们讨论了气体吸收,即利用组分在液体溶剂中的溶解度不同来分离气体混合物 的方法。这一章我们讨论互溶液体混合物的常用分离方法或说典型单元操作,液体蒸馏即精 馏。 9.1 蒸馏概述 蒸馏分离的依据 对混合物的分离方法总是利用其中各组分某种性质的差异,而用蒸馏分离 混合物的依据或说其原理是:虽然各液体组分都能挥发,但各组分挥发程度不同,有难有易, 于是在部分汽化时,气相中所含易挥发组分将比液相中的多,使原来的混合液达到某种程度 的分离。同理,当混合气部分冷凝时,冷凝液中所含的难挥发组分将比气相中的多,也能达 到一定程度的分离。当然,利用一次部分汽化和部分冷凝的分离是不充分的,但是可以利用 这一原理进行反复分离,达到要求的纯度。显然,在部分汽化和部分冷凝时,气液两相的组 成差别愈大,将愈有利于蒸馏分离。而气液两相共存时最终组成的关系属于相平衡问题。 总的说来,蒸馏是分离互溶液体混合物的操作,其依据是液相中组分的挥发度不同,所 进行的过程是部分汽化部分冷凝,两相共存的组成分配关系受相平衡制约。 习惯上,把混合物中易挥发的组分称为轻组分,难挥发的组分称为重组分。 工业蒸馏过程 ①按照操作方式分为间歇式和连续蒸馏; ②按蒸馏方法分为简单蒸馏,平衡蒸馏(闪馏),精馏和特殊精馏等; ③按操作压降分为常压、加压和减压精馏。比如在常压下为气态混合物,则可采用加压精馏; 沸点较高且为热敏性的物系可采用减压精馏。 按待分离物系中组分的数目可分为双(二元)组分和多组分精馏。工业中的精馏以多组 分精馏为主,但基本原理和计算与二元精馏无本质区别,所以本章着重讨论双组分常压精馏。 1

西北大学化工原理电子教案 蒸馏操作的费用和操作压强加热和冷却(能耗大)是蒸馏过程的主要费用。此外,对同样的 加热量和冷却量,所需费用还与加热温度和冷却温度有关。 9.2双组分溶液的汽液相平衡 蒸馏是汽液两相中的传质过程,因此常用组分在两相中浓度(组分)偏离平衡的程度来 衡量传质推动力的大小。传质过程是以两相达到相平衡为极限的。因此,汽液相平衡为极限 的。因此,汽液相平衡关系是分析蒸馏原理和设备计算的理论基础,所以在讨论精馏计算之 前,先讨论相平衡。 9.2.1理想物系的气液相平衡 气液两相平衡共存时的自由度根据相率,平衡物系的自由度为: F=N-Φ+2 (9-2) 对双组分物系气液:N=2、=2,则代入得: F=2 即双组分物系汽液平衡的自由度为2。 平衡物系的参数为温度T,压强P,以及汽相组成y和液相组成X。对二元系,给定一 个汽相组成和一个液相组成,则可由y4+yB=1,x4+xB=1定出另一个汽相组成和液相 组成。因而在上述四个参数T、P、y、x中任意确定两个,即可确定系统状态。 精馏系统经常在恒压下操作,即P一定,则在T、y、x中任意确定一个,系统的状态 就确定了。如果定x则y~T之间存在对应关系:如果定y,则x~T之间存在对应关系:如 果定T,则x~y之间存在对应关系。精馏过程中相平衡关系的定量描述,就是要找出P一 定时,y或x~T,以及y~x的定量关系。 完全理想物系是指:液相为理想溶液,服从拉乌尔定律,P,=Px:汽相为理想气体 服从道尔顿分压定律:P:=Py 在拉乌尔定律p,=px,中,p是纯组分i在溶液温度t下的饱和蒸汽压,因而p是 温度t的函数,可写成: pi=f() 纯组分的饱和蒸汽压P与温度t的关系通常用Antoine(安托因)经验方法计算,即: 2
西北大学化工原理电子教案 蒸馏操作的费用和操作压强 加热和冷却(能耗大)是蒸馏过程的主要费用。此外,对同样的 加热量和冷却量,所需费用还与加热温度和冷却温度有关。 9.2 双组分溶液的汽液相平衡 蒸馏是汽液两相中的传质过程,因此常用组分在两相中浓度(组分)偏离平衡的程度来 衡量传质推动力的大小。传质过程是以两相达到相平衡为极限的。因此,汽液相平衡为极限 的。因此,汽液相平衡关系是分析蒸馏原理和设备计算的理论基础,所以在讨论精馏计算之 前,先讨论相平衡。 9.2.1 理想物系的气液相平衡 气液两相平衡共存时的自由度 根据相率,平衡物系的自由度为: F=N-Φ+2 (9-2) 对双组分物系气液:N=2、Φ=2,则代入得: F=2 即双组分物系汽液平衡的自由度为 2。 平衡物系的参数为温度 T,压强 P,以及汽相组成 y 和液相组成 x。对二元系,给定一 个汽相组成和一个液相组成,则可由 + = 1 BA yy , + = 1 BA xx 定出另一个汽相组成和液相 组成。因而在上述四个参数 T、P、y、x 中任意确定两个,即可确定系统状态。 精馏系统经常在恒压下操作,即 P 一定,则在 T、y、x 中任意确定一个,系统的状态 就确定了。如果定 x 则 y~T 之间存在对应关系;如果定 y,则 x~T 之间存在对应关系;如 果定 T,则 x~y 之间存在对应关系。精馏过程中相平衡关系的定量描述,就是要找出 P 一 定时,y 或 x~T,以及 y~x 的定量关系。 完全理想物系是指:液相为理想溶液,服从拉乌尔定律, ;汽相为理想气体 服从道尔顿分压定律: i o ii = xpp = pyp ii 在拉乌尔定律 中, 是纯组分 i 在溶液温度 t 下的饱和蒸汽压,因而 是 温度 t 的函数,可写成: i o ii = xpp o i p o i p (tfp ) i o i = 纯组分的饱和蒸汽压 P 与温度 t 的关系通常用 Antoine (安托因)经验方法计算,即: 2

西北大学化工原理电子教案 10gp°=A-B (9-7) 1+C 式中A、B、C为经验常数,可用手册查出。 双组分理想物系的液相组成一温度(泡点)关系式 对双组分,由拉乌尔定律: PA=PAXA (9-3) P8=PBxB (9-4) 溶液沸腾时的蒸汽压之和等于外压P,则可得: PA+PB=P 即分压之和等于总压。由(93,4)式可得: Px+PaxB=P pxa+p8(1-x)=p x=p-pg (9-5) P-pa 或: x=-P-fo(t) (9-6) f0)-f() 此式即液相组成与泡点温度的关系。已知泡点温度t可直接由Acoine方程计算p?、pg则 求出x4。若己知x4,求t,则经试差。因为p与t的关系通常为非线性的。例见9-1。 气液两相平衡组成间的关系式联解拉乌尔式与道尔顿式即可得: 或对轻组分A写成: yA= (9-8) 若令两相平衡常数K为: K=P/p (9-10) 3
西北大学化工原理电子教案 Ct B Apo + log −= (9-7) 式中 A、B、C 为经验常数,可用手册查出。 双组分理想物系的液相组成-温度(泡点)关系式 对双组分,由拉乌尔定律: A (9-3) o AA = xpp B (9-4) o BB = xpp 溶液沸腾时的蒸汽压之和等于外压 P,则可得: ppp + BA = 即分压之和等于总压。由(9-3,4)式可得: B pxpxp o BA o A =+ ( A ) pxpxp o BA o A 1 =−+ o B o A o b A pp pp x − − = (9-5) ( ) () ()tftf tfp x A B B A − − 或: = (9-6) 此式即液相组成与泡点温度的关系。已知泡点温度 t 可直接由 Acoine 方程计算 、 则 求出 。若已知 ,求 t,则经试差。因为 与 t 的关系通常为非线性的。例见 9-1。 o pA o pB o A pi x A x 气液两相平衡组成间的关系式 联解拉乌尔式与道尔顿式即可得: i o i i x p p y = 或对轻组分 A 写成: A o A A x p p y = (9-8) 若令两相平衡常数κ 为: ppo κ = A (9-10) 3
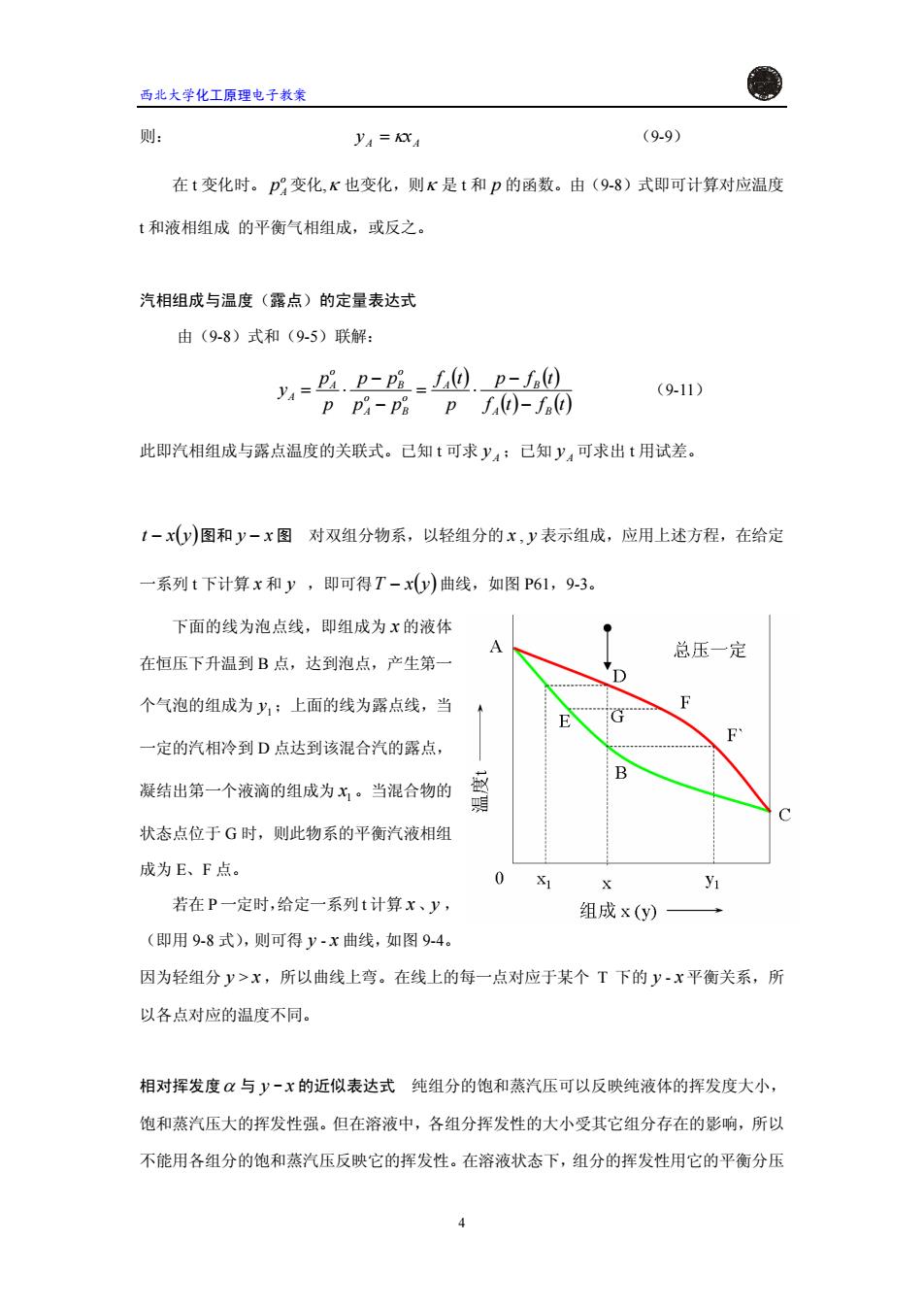
西北大学化工原理电子教案 则: y=KXA (9.9) 在t变化时。p变化,K也变化,则K是t和p的函数。由(9-8)式即可计算对应温度 t和液相组成的平衡气相组成,或反之。 汽相组成与温度(露点)的定量表达式 由(9-8)式和(9-5)联解: y=2.p-p=0.p-f0 (9-11) ppA-P8pf)-f@间 此即汽相组成与露点温度的关联式。己知t可求y4;己知y4可求出t用试差。 1-xy)图和y-x图对双组分物系,以轻组分的x,y表示组成,应用上述方程,在给定 一系列t下计算x和y,即可得T-xy)曲线,如图P61,93。 下面的线为泡点线,即组成为x的液体 A 总压一定 在恒压下升温到B点,达到泡点,产生第一 O 个气泡的组成为y,:上面的线为露点线,当 F E G 一定的汽相冷到D点达到该混合汽的露点, B 凝结出第一个液滴的组成为x。当混合物的 明 状态点位于G时,则此物系的平衡汽液相组 成为E、F点。 0 X yu 若在P一定时,给定一系列t计算x、y, 组成x(y) → (即用9-8式),则可得y-x曲线,如图9-4。 因为轻组分y>x,所以曲线上弯。在线上的每一点对应于某个T下的y-x平衡关系,所 以各点对应的温度不同。 相对挥发度与y-x的近似表达式纯组分的饱和蒸汽压可以反映纯液体的挥发度大小, 饱和蒸汽压大的挥发性强。但在溶液中,各组分挥发性的大小受其它组分存在的影响,所以 不能用各组分的饱和蒸汽压反映它的挥发性。在溶液状态下,组分的挥发性用它的平衡分压
西北大学化工原理电子教案 AA 则: = κxy (9-9) 在 t 变化时。 变化, o pA κ 也变化,则κ 是 t 和 p 的函数。由(9-8)式即可计算对应温度 t 和液相组成 的平衡气相组成,或反之。 汽相组成与温度(露点)的定量表达式 由(9-8)式和(9-5)联解: ( ) ( ) () ()tftf tfp p tf pp pp p p y A B A B o B o A o B o A A − − ⋅= − − ⋅= (9-11) 此即汽相组成与露点温度的关联式。已知 t 可求 ;已知 可求出 y A y A t 用试差。 − ( ) yxt 图和 y − x 图 对双组分物系,以轻组分的 x , y 表示组成,应用上述方程,在给定 一系列 t 下计算 x 和 y ,即可得 − (yxT )曲线,如图 P61,9-3。 下面的线为泡点线,即组成为 x 的液体 在恒压下升温到 B 点,达到泡点,产生第一 个气泡的组成为 ;上面的线为露点线,当 一定的汽相冷到 D 点达到该混合汽的露点, 凝结出第一个液滴的组成为 。当混合物的 状态点位于 G 时,则此物系的平衡汽液相组 成为 E、F 点。 1 y 1 x 若在 P 一定时,给定一系列 t 计算 x 、 , (即用 9-8 式),则可得 - y y x 曲线,如图 9-4。 因为轻组分 y > x ,所以曲线上弯。在线上的每一点对应于某个 T 下的 y - x 平衡关系,所 以各点对应的温度不同。 相对挥发度α 与 - y x 的近似表达式 纯组分的饱和蒸汽压可以反映纯液体的挥发度大小, 饱和蒸汽压大的挥发性强。但在溶液中,各组分挥发性的大小受其它组分存在的影响,所以 不能用各组分的饱和蒸汽压反映它的挥发性。在溶液状态下,组分的挥发性用它的平衡分压 4

西北大学化工原理电子教案 ● 与其液相分率的比值表示,并称为挥发度,即: "4sP4 XA XB 若对纯组分,x4=1,平衡分压即为挥发度,也即是饱和蒸汽压。 相对挥发度定义为两组分挥发度之比,即: a==Palx (9-12) VB PB/XB 若气相服从道尔顿分压定律P,=py,则: a=yalya (9-13) XA/XB 即气相中两组分的浓度比为液相中两组分浓度比的α倍。α的定义式即(9-13) 对双组分物系,由y4+yB=1,x4+xg=1,代入并解出y(以轻组分表示)则得: OX y=1+(a-1x (9-14) 此式也称为相平衡方程。如果能知道α,则可计算互成平衡时易挥发组分的y-x对应关系。 此式在精馏计算中用的最多。 对液相为理想溶液的完全理想体系,拉乌尔定律适用。P,=px,则: a=Palxs=Pi (9-15) Pa/x8 pe 即对完全理想体系,α的大小依赖于各组分的性质。由于p?与pg均是温度的函数,则也 是温度的函数,但α随温度的变化比p?,pg随温度的变化小的多。因而在工程设计中取α 的某一平均值计算y一x关系颇为方便。 平均相对挥发度的取法常用如下两种方式: ①算术平均am 当在操作温度的上下限范围内α变化不大时。可取上限温度心,和下限温度,的算术平 均值作为整个温度范围内的am平均值,即:
西北大学化工原理电子教案 与其液相分率的比值表示,并称为挥发度,即: A A A x p v = B B B x p v = 若对纯组分, ,平衡分压即为挥发度,也即是饱和蒸汽压。 = 1 A x 相对挥发度定义为两组分挥发度之比,即: BB AA B A xp xp v v α == (9-12) 若气相服从道尔顿分压定律 = pyp ii ,则: BA BA xx yy α = (9-13) 即气相中两组分的浓度比为液相中两组分浓度比的α 倍。 α 的定义式即(9-13) 对双组分物系,由 =+ 1, y BA yy + = 1 BA xx ,代入并解出 (以轻组分表示)则得: ( )x x y −+ 11 = α α (9-14) 此式也称为相平衡方程。如果能知道α ,则可计算互成平衡时易挥发组分的 y - x 对应关系。 此式在精馏计算中用的最多。 对液相为理想溶液的完全理想体系,拉乌尔定律适用。 i 则: o ii = xpp o B o A BB AA p p xp xp α == (9-15) 即对完全理想体系,α 的大小依赖于各组分的性质。由于 与 均是温度的函数,则 o pA o pB α 也 是温度的函数,但α 随温度的变化比 , 随温度的变化小的多。因而在工程设计中取 o pA o pB α 的某一平均值计算 y − x 关系颇为方便。 平均相对挥发度的取法常用如下两种方式: ① 算术平均α m 当在操作温度的上下限范围内α 变化不大时。可取上限温度α1和下限温度α 2的算术平 均值作为整个温度范围内的α m 平均值,即: 5

西北大学化工原理电子教案 a-a+a) (9-16) 2 ②内插平均 当温度变化范围内α变化较高,但<30%时,可取: a=a+(az-a)x (9-17) a1,2仍为两个温度下的相对挥发度,则给定一系列x, 1.0 =5 可求出一系列。代入(9-14)相平衡方程,可求出一系列y, 3 则可得y-x图。 a=1,(y=x) 相对挥发度α愈大,同一液相组成对应的平衡汽相浓度 愈大。所以α的大小可作为蒸馏分离某个物系难易程度的标 1.0 准。化愈大,蒸馏分离越容易。 0 X 相对挥发度4为定值时的相平衡曲线(恒压) 9.2.2非理想物系的汽液平衡 上面讨论了理想物系的汽液平衡,它对物性比较相近的物系近似准确。比如苯甲苯, 甲醇-乙醇等物系。但在实际蒸馏物系中,绝大部分是非理想物系。溶液的非理想主要来源 于异种分子之间的不同作用力,其宏观表现在与拉乌尔定律的偏差。 汽液相平衡的非理想物系问题是非常复杂的。它可能是:汽相非理想溶液-液相非理想 溶液:液相非理想溶液汽相理想溶液:汽相理想溶液-液相非理想溶液等。这些物系的相平 衡问题将在化工热力学中逐一讨论,此处仅定性讨论非理想物系的相图以及汽相为理想气 体,液相为非理想溶液的汽液平衡计算。 非理想溶液实际溶液与理想溶液的偏差采用溶液系数来描述,活度系数定义为: x:fx ā,为实际溶液的活度:了为i组分在液相中的逸度,∫为i组分在纯态时的逸度。对汽相 为理想气体,在达到平衡时: ==p, =p 6
西北大学化工原理电子教案 ( 21 2 1 m += ααα ) (9-16) ②内插平均 当温度变化范围内α 变化较高,但<30%时,可取: ( )x α = α + α −α121 (9-17) x α1,α 2 仍为两个温度下的相对挥发度,则给定一系列 , 可求出一系列α 。代入(9-14)相平衡方程,可求出一系列 , 则可得 - y y x 图。 相对挥发度α 愈大,同一液相组成对应的平衡汽相浓度 愈大。所以α 的大小可作为蒸馏分离某个物系难易程度的标 准。α 愈大,蒸馏分离越容易。 9.2.2 非理想物系的汽液平衡 上面讨论了理想物系的汽液平衡,它对物性比较相近的物系近似准确。比如苯-甲苯, 甲醇-乙醇等物系。但在实际蒸馏物系中,绝大部分是非理想物系。溶液的非理想主要来源 于异种分子之间的不同作用力,其宏观表现在与拉乌尔定律的偏差。 汽液相平衡的非理想物系问题是非常复杂的。它可能是:汽相非理想溶液-液相非理想 溶液;液相非理想溶液-汽相理想溶液;汽相理想溶液-液相非理想溶液等。这些物系的相平 衡问题将在化工热力学中逐一讨论,此处仅定性讨论非理想物系的相图以及汽相为理想气 体,液相为非理想溶液的汽液平衡计算。 非理想溶液 实际溶液与理想溶液的偏差采用溶液系数来描述,活度系数定义为: i L i L i i i i xf f x a ) ) γ == L i f ) ai ) 为实际溶液的活度; 为 i 组分在液相中的逸度, 为 i 组分在纯态时的逸度。对汽相 为理想气体,在达到平衡时: L i f i V i L i == pff) ) o i L i = pf 6

西北大学化工原理电子教案 ● 则: Yi=Pilpx 则: P=PxYi (9-18) 若汽相服从道尔顿定律:P,=py,则: y.=Pixy (9-20) p Y,为i组分的活度系数,它与T、P以及液相组成有关,可由实验测定或热力学关系计算。 在以知y,的情况下,可求出1-y(x)或y-x关系曲线。 溶液的非理想性用活度系数来描述,在实际中有两大类非理想溶液,即:()Y,>】对 理想溶液呈正偏差的非理想溶液:和(b)Y,1,而当易挥发组分含量超过共沸点组成后,则C
西北大学化工原理电子教案 i o iii 则: γ = xpp 则: ii (9-18) o ii = xpp γ 若汽相服从道尔顿定律: 则: = pyp ii i i o i i p xp y = γ (9-20) i γ 为 i 组分的活度系数,它与 T、P 以及液相组成有关,可由实验测定或热力学关系计算。 在以知 i γ 的情况下,可求出 或 − ( ) xyt y − x 关系曲线。 i 溶液的非理想性用活度系数来描述,在实际中有两大类非理想溶液,即:(a)γ >1 对 理想溶液呈正偏差的非理想溶液;和(b) i γ 1,而当易挥发组分含量超过共沸点组成后,则α <1,在共沸点α =1。故对于这 类物系不能用简单精馏的方法同时获得两种纯组分,在精馏塔顶只能获得共沸混合物。 4、 具有负偏差且具有最高共沸点 x B γ A 和γ 均小于 1,而且数值较小,即对于理想溶液具有负偏差。在恒压的 t- 图上出 现极大值,它们具有最高共沸点,比相应的两种纯组分的沸点都高。当易挥发组分的含量小 7

西北大学化工原理电子教案 于共沸组成时心>1,而当易挥发组分的含量大于共沸组成时:<1,在共沸点时=1。对 此类溶液也不能用简单精馏的方法获得两种纯组分,在塔底只能得到最高恒沸物。 总压对相平衡的影响以上关于相平衡的讨论的y-x,~x图均以P恒定为前提。对同一物 系,混合物的泡点愈高,各组分间挥发度的差异愈小。因此,蒸馏操作的压强愈高,泡点也 随之升高,相对挥发度降低,分离困难。 在蒸馏操作中,当总压低于两纯组分的临界压强,蒸馏可在全浓度范围内操作。当压强 高于轻组分的临界压强时,汽液两相共存区缩小,蒸馏分离只能在一定浓度范围内进行,不 可能得到轻组分的高纯度产物。 实际所用汽液平衡数据一般由实验测定,可查手册或专著。 9.3平衡蒸馏与简单蒸馏 9.3.1平衡蒸馏 使混合物汽液两相共存,达到平衡,再将两相分开,以使混合物得到一定程度分离的 蒸馏方式称为平衡蒸馏。 生产中应用的连续平衡蒸馏装置,料液送到加热器中升温,使液体温度高于分离器压 力下的沸点,通过减压阀,过热液体发生自蒸发,使部分液体汽化,这种过程称为闪蒸。然 后平衡的汽液两相在分离器中分开,汽相为顶部产物其中易挥发组分较为富集。液相为底部 产物,其中难挥发组分获得增浓。 过程的数学描述蒸馏过程的数学描述主要是物料衡算,能量衡算和相平衡关系。 1、物料衡算 对连续定态过程列出总物料衡算式为: F=D+W (9-21) 对易挥发组分: Fx =Dy+Wx (9-22) 将D=FW代入(9-22)式的:
西北大学化工原理电子教案 于共沸组成时 α >1,而当易挥发组分的含量大于共沸组成时α <1,在共沸点时α =1。对 此类溶液也不能用简单精馏的方法获得两种纯组分,在塔底只能得到最高恒沸物。 总压对相平衡的影响 以上关于相平衡的讨论的 y - x ,t- x 图均以 P 恒定为前提。对同一物 系,混合物的泡点愈高,各组分间挥发度的差异愈小。因此,蒸馏操作的压强愈高,泡点也 随之升高,相对挥发度降低,分离困难。 在蒸馏操作中,当总压低于两纯组分的临界压强,蒸馏可在全浓度范围内操作。当压强 高于轻组分的临界压强时,汽液两相共存区缩小,蒸馏分离只能在一定浓度范围内进行,不 可能得到轻组分的高纯度产物。 实际所用汽液平衡数据一般由实验测定,可查手册或专著。 9.3 平衡蒸馏与简单蒸馏 9.3.1 平衡蒸馏 使混合物汽液两相共存,达到平衡,再将两相分开,以使混合物得到一定程度分离的 蒸馏方式称为平衡蒸馏。 生产中应用的连续平衡蒸馏装置,料液送到加热器中升温,使液体温度高于分离器压 力下的沸点,通过减压阀,过热液体发生自蒸发,使部分液体汽化,这种过程称为闪蒸。然 后平衡的汽液两相在分离器中分开,汽相为顶部产物其中易挥发组分较为富集。液相为底部 产物,其中难挥发组分获得增浓。 过程的数学描述 蒸馏过程的数学描述主要是物料衡算,能量衡算和相平衡关系。 1、 物料衡算 对连续定态过程列出总物料衡算式为: += WDF (9-21) 对易挥发组分: WxDyFx f = + (9-22) 将 D=F-W 代入(9-22)式的: x F W y F W x f ⎟ + ⎠ ⎞ ⎜ ⎝ ⎛ 1−= 8

西北大学化工原理电子教案 ● W 令q= F 即液相产物占进料的分率,则: y=-,9x+ 1-g1-q9 x,=(1-q)y+qx 或: y=9x-1 X (9-23) 1-g1-q 式中: 0-0=2 为汽化率。(9-23)即为物料平衡方程。 2、热量衡算 加热炉的热量Q为: Q=FCp(T-to) 节流减压后,物料放出的热量供自身部分汽化, Fc(T-t)=(1-q)FY 则物料加热温度T为: T=4+0-9 (9-25) 3、过程特征方程: 平衡蒸馏中两相平衡,y与x应满足相平衡方程:y=x) (9-26) 对理想溶液 y= (9-26) 1+(a-1x 平衡温度与组成x应满足泡点方程,即 1。=(x) (9-27) 此特征方程均属相平衡方程。 平衡蒸馏过程计算在闪蒸计算中,通常给定F、x,即D或L,求y或x,即气相和液相组 成。计算的原则是联立物料衡算和相平衡方程,即(9-23)和(9-24)联立解出y和x。如 果是理想溶液,且为常数,则计算非常简单。如果是非理想溶液,在一定P下作出相平衡 曲线y-x图,代表两相平衡的塔顶及塔底组成y和x在y-x曲线上,又在代表物料衡算的直 9
西北大学化工原理电子教案 F W 令 q = 即液相产物占进料的分率,则: q x x q q y F − + − −= 11 ( ) qxyqx f = 1− + F x q x q q y − − − = 1 1 1 或: (9-23) ( ) F D 式中: 1 q =− 为汽化率。(9-23)即为物料平衡方程。 2、 热量衡算 加热炉的热量 Q 为: Q=FCp(T-t0) 节流减压后,物料放出的热量供自身部分汽化, ( )( )FqtTFc γ ep =− 1− 则物料加热温度 T 为: ( ) p e c qtT γ 1−+= (9-25) 3、 过程特征方程: 平衡蒸馏中两相平衡,y 与 x 应满足相平衡方程:y=f(x) (9-26) ( )x x y −+ 11 = α α 对理想溶液 (9-26’) 平衡温度与组成 x 应满足泡点方程,即 ( ) xt e = φ (9-27) 此特征方程均属相平衡方程。 平衡蒸馏过程计算 在闪蒸计算中,通常给定 F、 即 D 或 L,求 y 或 x ,即气相和液相组 成。计算的原则是联立物料衡算和相平衡方程,即(9-23)和(9-24)联立解出 y 和 x。如 果是理想溶液,且 a 为常数,则计算非常简单。如果是非理想溶液,在一定 P 下作出相平衡 曲线 y-x 图,代表两相平衡的塔顶及塔底组成 y 和 x 在 y-x 曲线上,又在代表物料衡算的直 f x 9

西北大学化工原理电子教案 线方程(923)上。将(9-23)方程与yx图上作直线,斜率为9,并过点x=x、y=y 9-1 即f点。操作线与平衡线的交点为e点,e点对应的平衡浓度即y和x,所以e点即满足平 衡线又满足操作线。 对非理想溶液,还可以画出泡点组成图,由此求出相应x下的t。,将t。代入(9-25)式 求出T,再代入(9-24)式求出Q,即可求出所需热流量。 9.3.2简单蒸馏 简单蒸馏,是混合液在加热(蒸馏)釜中逐渐汽化,产生的蒸汽随即进入冷凝器,而不 断得到馏出液,放入容器的不同贮槽内。由于y>x,馏出液含易挥发组分较富,因而釜内溶 液易挥发组分的浓度(组成)x将随时间延续而逐渐降低。这样又使得与x平衡的蒸汽组成 y(即馏出液的组成)亦随时间变化(降低),而釜内溶液的沸点则逐渐升高。由此可见这种 蒸馏方式是不稳定的,需分批进行。由于馏出液中易挥发组分浓度逐渐降低,所以要用几个 贮槽分别得到不同时间下馏出液。 简单精馏可用于初步分离,特别对相对挥发度大的混合物进行分离颇为有效。比如从含 乙醇不到10%的发酵液中,经一次蒸馏可得到50°的烧酒。要得到60~65的烧酒,可再蒸 馏一次。 简单蒸馏的数学描述在简单蒸馏的计算中,①生产能力根据热负荷和传热能力计算:②而 馏出液量,馏出液浓度,残液的浓度与量之间的关系由物料衡算确定。 由于简单精馏是非定态的,则需考虑微分物料衡算。设:W为某瞬时釜内的液体量,x 为某瞬时釜内的液体的浓度:y为某瞬时由釜中蒸出的汽相浓度。则在dπ时间内,釜内蒸 出的物料量为,则釜内料液量为 w-dw 液相组成降为:x-d 则釜液中含易挥发组分的量为:(w-h)(x-d) 则在dπ时间内易挥发组分的物料衡算为: wx=(w-dwx-dx)+ydw 略去高阶无穷小量d小vdk,并分离变量得: 10
西北大学化工原理电子教案 q −1 q 线方程(9-23)上。将(9-23)方程与 y-x 图上作直线,斜率为- ,并过点 、 , 即 f 点。操作线与平衡线的交点为 e 点,e 点对应的平衡浓度即 y 和 x,所以 e 点即满足平 衡线又满足操作线。 f = xx f = yy 对非理想溶液,还可以画出泡点组成图,由此求出相应 x 下的 ,将 代入(9-25)式 求出 T,再代入(9-24)式求出 Q,即可求出所需热流量。 e t e t 9.3.2 简单蒸馏 简单蒸馏,是混合液在加热(蒸馏)釜中逐渐汽化,产生的蒸汽随即进入冷凝器,而不 断得到馏出液,放入容器的不同贮槽内。由于 y>x,馏出液含易挥发组分较富,因而釜内溶 液易挥发组分的浓度(组成)x 将随时间延续而逐渐降低。这样又使得与 x 平衡的蒸汽组成 y(即馏出液的组成)亦随时间变化(降低),而釜内溶液的沸点则逐渐升高。由此可见这种 蒸馏方式是不稳定的,需分批进行。由于馏出液中易挥发组分浓度逐渐降低,所以要用几个 贮槽分别得到不同时间下馏出液。 简单精馏可用于初步分离,特别对相对挥发度大的混合物进行分离颇为有效。比如从含 乙醇不到 10%的发酵液中,经一次蒸馏可得到 50°的烧酒。要得到 60~65°的烧酒,可再蒸 馏一次。 简单蒸馏的数学描述 在简单蒸馏的计算中,①生产能力根据热负荷和传热能力计算;②而 馏出液量,馏出液浓度,残液的浓度与量之间的关系由物料衡算确定。。 由于简单精馏是非定态的,则需考虑微分物料衡算。设:W为某瞬时釜内的液体量,x 为某瞬时釜内的液体的浓度;y 为某瞬时由釜中蒸出的汽相浓度。则在dτ 时间内,釜内蒸 出的物料量为 dw,则釜内料液量为 − dww 液相组成降为: − dxx 则釜液中含易挥发组分的量为:( − dww )( − dxx ) 则在 dτ 时间内易挥发组分的物料衡算为: ( )( ) −= − + ydwdxxdwwwx 略去高阶无穷小量 dwdx ,并分离变量得: 10