
西北大学化工原理电子教案 1.流体流动 流体流动是最普遍的化工单元操作之一,研究流体流动问题也是研究其它化工单元操作 的重要基础。涉及流体流动规律的主要方面有: (1)流动阻力及流量计量 各种流体的输送,需要进行管路的设计、输送机械的选择以及 所需功率的计算。 (2)流动对传热、传质及化学反应的影响 化工设备中的传热、传质以及反应过程在很大 程度上受流体在设备内流动状况的影响。 (3)流体的混合流体与流体、流体与固体颗粒在各类化工设备中的混合效果都受流体流 动的基本规律的支配。 1.1概述 1.1.1流体流动的考察方法 连续性假定流体包括液体和气体。流体是由大量的彼此之间有一定间隙的单个分子所组 成,而且各单个分子作着随机的、混乱的运动。在工程上,在研究流体流动时,常从宏观出 发,将流体视为由无数流体质点(或微团)组成的连续介质。所谓质点指的是一个含有大量 分子的流体微团,其尺寸远小于设备尺寸但比起分子自由程却要大得多。假定流体是由大量 质点组成的、彼此间没有间隙、完全充满所占空间的连续介质。流体的物理性质及运动参数 在空间作连续分布,从而可以使用连续函数的数学工具加以描述。流体在运动时,各质点可 改变其相对位置。 注意:这样的连续性假定在绝大多数情况下是适合的:然而,在高真空稀薄气体的情况 下,这样的假定将不复成立。 运动的描述方法一拉格朗日法和欧拉法 拉格朗日法:选定一个流体质点,对其跟踪观察,描述其运动参数(如位移、速度等) 与时间的关系。 欧拉法:不跟踪流体质点进行观察,而是在固定空间位置上观察流体质点的运动情况, 如空间各点的速度、压强、密度等,即欧拉法系直接描述各有关运动参数在空间各点的分布 情况和随时间的变化。例如,对于速度,可作如下描述:
西北大学化工原理电子教案 1. 流体流动 流体流动是最普遍的化工单元操作之一,研究流体流动问题也是研究其它化工单元操作 的重要基础。涉及流体流动规律的主要方面有: (1) 流动阻力及流量计量 各种流体的输送,需要进行管路的设计、输送机械的选择以及 所需功率的计算。 (2) 流动对传热、传质及化学反应的影响 化工设备中的传热、传质以及反应过程在很大 程度上受流体在设备内流动状况的影响。 (3) 流体的混合 流体与流体、流体与固体颗粒在各类化工设备中的混合效果都受流体流 动的基本规律的支配。 1.1 概述 1.1.1 流体流动的考察方法 连续性假定 流体包括液体和气体。流体是由大量的彼此之间有一定间隙的单个分子所组 成,而且各单个分子作着随机的、混乱的运动。在工程上,在研究流体流动时,常从宏观出 发,将流体视为由无数流体质点(或微团)组成的连续介质。所谓质点指的是一个含有大量 分子的流体微团,其尺寸远小于设备尺寸但比起分子自由程却要大得多。假定流体是由大量 质点组成的、彼此间没有间隙、完全充满所占空间的连续介质。流体的物理性质及运动参数 在空间作连续分布,从而可以使用连续函数的数学工具加以描述。流体在运动时,各质点可 改变其相对位置。 注意:这样的连续性假定在绝大多数情况下是适合的;然而,在高真空稀薄气体的情况 下,这样的假定将不复成立。 运动的描述方法-拉格朗日法和欧拉法 拉格朗日法:选定一个流体质点,对其跟踪观察,描述其运动参数(如位移、速度等) 与时间的关系。 欧拉法:不跟踪流体质点进行观察,而是在固定空间位置上观察流体质点的运动情况, 如空间各点的速度、压强、密度等,即欧拉法系直接描述各有关运动参数在空间各点的分布 情况和随时间的变化。例如,对于速度,可作如下描述: 1

西北大学化工原理电子教案 ux=fx,y二,) 4=fxy三, (1-1) 4=Ex,g二,) 拉格朗日法描述的是同一质点在不同时刻的状态:欧拉法描述的则是空间各点的状态及 其与时间的关系。 注意:此处所谓的点不是真正几何意义上的点,而是具有质点尺寸的点。 定态流动如果运动空间各点的状态不随时间而变化,则该流动称为定态流动。显然,对 定态流动,指定点的速度以及压强等均为常数而与时间无关。例如,对速度: Ou=0: =0:0=0. 流线与轨线 轨线是某一流体质点的运动轨迹,是采用拉格朗日法考察流体运动所得的结果。 流线是采用欧拉法考察的结果,流线上各点的切线表示同一时刻各点的速度方向。 轨线与流线是完全不同的。轨线描述的是同一质点在不同时间的位置,而流线表示的则 是同一瞬间不同质点的速度方向。在定态流动时流线与轨线重合:各流线不会相交。 图1-1流线 系统与控制体 系统(或物系)一包含众多流体质点的集合。 ●系统的边界一系统与外界之间的分界面。 ·系统与外界可以有力的作用与能量的交换,但没有质量交换。系统的边界随着流体 一起运动,因而其形状和大小都可随时间而变化。 系统是采用拉格朗日法考察流体的
西北大学化工原理电子教案 ux=fx(x, y, z, t) uy=fy(x, y, z, t) (1-1) uz=fz(x, y, z, t) 拉格朗日法描述的是同一质点在不同时刻的状态;欧拉法描述的则是空间各点的状态及 其与时间的关系。 注意:此处所谓的点不是真正几何意义上的点,而是具有质点尺寸的点。 定态流动 如果运动空间各点的状态不随时间而变化,则该流动称为定态流动。 显然, 对 定态流动,指定点的速度以及压强等均为常数而与时间无关。例如,对速度: = 0 ∂ ∂ t ux ; = 0 ∂ ∂ t uy ; = 0 ∂ ∂ t uz 。 流线与轨线 轨线是某一流体质点的运动轨迹,是采用拉格朗日法考察流体运动所得的结果。 流线是采用欧拉法考察的结果,流线上各点的切线表示同一时刻各点的速度方向。 轨线与流线是完全不同的。轨线描述的是同一质点在不同时间的位置,而流线表示的则 是同一瞬间不同质点的速度方向。在定态流动时流线与轨线重合;各流线不会相交。 图 1-1 流线 系统与控制体 系统(或物系)-包含众多流体质点的集合。 z 系统的边界-系统与外界之间的分界面。 z 系统与外界可以有力的作用与能量的交换,但没有质量交换。系统的边界随着流体 一起运动, 因而其形状和大小都可随时间而变化。 z 系统是采用拉格朗日法考察流体的。 2

西北大学化工原理电子教案 控制体一划定一固定的空间体积来考察问题,该空间体积。 ●控制面一构成控制体的空间界面。 ●控制面总是封闭的固定界面:流体可以自由进出控制体,控制面上可以有力的作用 与能量的交换。 。控制体是采用欧拉法考察流体的。 考察方法的选择对流体流动多采用欧拉法。 1.1.2流体流动中的作用力 体积力体积力作用于流体的每一个质点上,并与流体的质量成正比,所以也称质量力,对 于均质流体也与流体的体积成正比。如:流体在重力场运动时受到的重力。 表面力一压力与剪力表面力与表面积成正比。若取流体中任一微小平面,作用于其上的表 面力可分为垂直于表面的力和平行于表面的力。前者称为压力,后者称为剪力(或切力)。 单位面积上所受的压力称为压强:单位面积上所受的剪力称为剪应力。 压强的单位单位为N/m2,也称为帕斯卡(Pa)。现工程上常用兆帕作压强的计量单位。 1MPa(兆帕)=10Pa 剪应力设有间距甚小的两平行平板间充满流体(图1-2)。下板固定,上板施加一平行于 平板的切向力F使此平板以速度作匀速运动。紧贴于运动板上方的流体层以同一速度” 流动,而紧贴于固定板上方的流体层则静止不动。两板间各层流体的速度不同,其大小如图 中箭头所示。单位面积的切向力(FA)即为流体的剪应力。对大多数流体,剪应力服从 下列牛顿粘性定律: du T=H (1-2) dy 式中: 为法向速度梯度,1/s: dy u为流体的粘度,Ns/m2,即Pas: x为剪应力,Pa
西北大学化工原理电子教案 控制体-划定一固定的空间体积来考察问题,该空间体积。 z 控制面-构成控制体的空间界面。 z 控制面总是封闭的固定界面;流体可以自由进出控制体,控制面上可以有力的作用 与能量的交换。 z 控制体是采用欧拉法考察流体的。 考察方法的选择 对流体流动多采用欧拉法。 1.1.2 流体流动中的作用力 体积力 体积力作用于流体的每一个质点上,并与流体的质量成正比,所以也称质量力, 对 于均质流体也与流体的体积成正比。如:流体在重力场运动时受到的重力。 表面力-压力与剪力 表面力与表面积成正比。若取流体中任一微小平面,作用于其上的表 面力可分为垂直于表面的力和平行于表面的力。前者称为压力,后者称为剪力(或切力)。 单位面积上所受的压力称为压强;单位面积上所受的剪力称为剪应力。 压强的单位 单位为 N/m2 ,也称为帕斯卡(Pa)。现工程上常用兆帕作压强的计量单位。 1MPa(兆帕)= 106 Pa 剪应力 设有间距甚小的两平行平板间充满流体(图 1-2)。下板固定,上板施加一平行于 平板的切向力 F 使此平板以速度 u 作匀速运动。紧贴于运动板上方的流体层以同一速度 u 流动,而紧贴于固定板上方的流体层则静止不动。两板间各层流体的速度不同,其大小如图 中箭头所示。单位面积的切向力(F/A)即为流体的剪应力τ。对大多数流体,剪应力τ服从 下列牛顿粘性定律: dy du = μτ (1-2) 式中: dy du 为法向速度梯度,1/s; μ为流体的粘度,N·s/m2 ,即 Pa·s; τ为剪应力,Pa。 3

西北大学化工原理电子教案 香 7 图1-2剪应力与速度梯度 牛顿粘性定律指出:剪应力与法向速度梯度成正比,与法向压力无关。流体的这一规律 与固体表面的摩擦力的规律截然不同,固体的剪应力正比于剪切变形。速度梯度就是剪切变 形的速率。如图1-3所示, u+du dy 图1-3变形率 在流动流体中取一流体微元,经d!时间后发生剪切变形,角变形d为:d0= dudt dy 单位时间变形是: dodu (1-3) dt dy 可见ddy是一维流动中因剪切而造成的角变形速率,简称剪切率。运动着的粘性流体 内部的剪切力亦称为内摩擦力。 静止流体是不能承受剪应力和抵抗剪切变形的,这是流体与固体力学特性又一不同点。 粘度是流体流动时在与流动方向垂直的方向上产生单位速度梯度所需的剪应力。 图1-4粘性流体在管内的速度分布 图1-5理想流体在管内的速度分布 粘性的物理本质是分子间的引力和分子的运动与碰撞。流体的粘度是温度和压力的函 数。通常液体的粘度随温度增加而减小:压力对液体粘度的影响不显著。气体的粘度成百倍 地小于液体的粘度,而且随温度呈现相反的变化,气体的粘度随温度上升而增大:气体的粘
西北大学化工原理电子教案 x y F u 图 1-2 剪应力与速度梯度 牛顿粘性定律指出:剪应力与法向速度梯度成正比,与法向压力无关。流体的这一规律 与固体表面的摩擦力的规律截然不同,固体的剪应力正比于剪切变形。速度梯度就是剪切变 形的速率。如图 1-3 所示, 图 1-3 变形率 在流动流体中取一流体微元,经 dt 时间后发生剪切变形,角变形 dθ为: dy dudt dθ = 单位时间变形是: dy du dt d = θ (1-3) 可见 du/dy 是一维流动中因剪切而造成的角变形速率,简称剪切率。运动着的粘性流体 内部的剪切力亦称为内摩擦力。 静止流体是不能承受剪应力和抵抗剪切变形的,这是流体与固体力学特性又一不同点。 粘度是流体流动时在与流动方向垂直的方向上产生单位速度梯度所需的剪应力。 图 1-4 粘性流体在管内的速度分布 图 1-5 理想流体在管内的速度分布 粘性的物理本质是分子间的引力和分子的运动与碰撞。流体的粘度是温度和压力的函 数。通常液体的粘度随温度增加而减小;压力对液体粘度的影响不显著。气体的粘度成百倍 地小于液体的粘度,而且随温度呈现相反的变化,气体的粘度随温度上升而增大;气体的粘 dθ u+du dy u 4

西北大学化工原理电子教案 度随压力的上升而增大。 粘度的单位是Pas,较早的手册也常用泊(达因秒/厘米)或厘泊(0.01泊)表示。其 间的关系为:1厘泊(cP)=103Pas。 运动粘度()定义为粘度与密度p的比值,即 (1-4) p 其单位为ms。为示区别,粘度又称为动力粘度。 牛顿型流体:剪应力与速度梯度的关系符合牛顿粘性定律的流体: 非牛顿型流体:不符合牛顿粘性定律的流体。 1.1.3流体流动中的机械能 流体所含的能量包括内能和机械能。 内能:储存与物质内部的机械能,内能由流体本身的状态决定。 机械能=位能+动能+压强能 流体自低压向高压对抗压力流动时,流体将有此而获得能量,这种能量称作压强能。 流体流动时将存在着三种机械能的相互转换。流体粘性所造成的剪力可看作是一种内摩 擦力,它将消耗部分机械能使之转化为热能而耗失。因此,流体的粘性使流体在流动过程中 产生机械能损失。为了实现流体的输送,还常需输送机械提供必需的能量,即总机械能=位 能+动能+压强能+能量损失。 1.2流体静力学 1.21静压强在空间的分布 静压强在静止流体中,作用于某一点不同方向上的压强在数值上是相等的,即一点的压强 只要说明它的数值即可。空间各点的静压强其数值不同,可以用如下的方程描述: p=f(x.y.=) (1-5) 流体微元的受力平衡设从静止流体中取一立方体流体微元,其中心点A的坐标为(x,y:。 立方体各边分别与坐标轴ox、oy、oz平行,边长分别为、、金,如图1-6所示。 (1)表面力设六面体中心点A处的静压强为p,沿x方向作用于abcd面上的压强为 5
西北大学化工原理电子教案 度随压力的上升而增大。 粘度的单位是 Pa⋅s,较早的手册也常用泊(达因⋅秒/厘米)或厘泊(0.01 泊)表示。其 间的关系为:1 厘泊(cP)= 10-3 Pa·s。 运动粘度(ν)定义为粘度μ与密度ρ的比值,即 ρ μ ν = (1-4) 其单位为m 2 /s。为示区别,粘度μ又称为动力粘度。 牛顿型流体:剪应力与速度梯度的关系符合牛顿粘性定律的流体; 非牛顿型流体:不符合牛顿粘性定律的流体。 1.1.3 流体流动中的机械能 流体所含的能量包括内能和机械能。 内能:储存与物质内部的机械能,内能由流体本身的状态决定。 机械能=位能+动能+压强能 流体自低压向高压对抗压力流动时,流体将有此而获得能量,这种能量称作压强能。 流体流动时将存在着三种机械能的相互转换。流体粘性所造成的剪力可看作是一种内摩 擦力,它将消耗部分机械能使之转化为热能而耗失。因此,流体的粘性使流体在流动过程中 产生机械能损失。为了实现流体的输送,还常需输送机械提供必需的能量,即总机械能=位 能+动能+压强能+能量损失。 1.2 流体静力学 1.2.1 静压强在空间的分布 静压强 在静止流体中,作用于某一点不同方向上的压强在数值上是相等的,即一点的压强 只要说明它的数值即可。空间各点的静压强其数值不同,可以用如下的方程描述: p = f (x, y, z) (1-5) 流体微元的受力平衡 设从静止流体中取一立方体流体微元,其中心点 A 的坐标为( x, y, z )。 立方体各边分别与坐标轴 ox、oy、oz 平行,边长分别为δx、δy、δz,如图 1-6 所示。 (1) 表面力 设六面体中心点 A 处的静压强为 p,沿 x 方向作用于 abcd 面上的压强为 5

西北大学化工原理电子教案 1 众,作用于abc过面上的压强为P+×必x.因此作用于该两表面上的 20x 2 Ox 压力分别为: op Sx 2 图1-6流体微元的受力平衡 (2)体积力设作用于单位质量流体上的体积力在x方向的分量为X,则微元所受的体积力 在x方向的分量为Xp远(式中p为密度)。同理,在y及:轴上微元所受的体积力分别 为YpoxSv&Y和Zp&x8v&。 该流体处于静止状态,外力之和必等于零。对x方向,可写成: p--(p+5正+=0 各项均除以微元体的流体质量py正可得: X-1@p 0 p ox 同理 y-1p=0 (1-6) pay z、1 =0 poz 此式称为欧拉平衡方程。等式左方为单位质量流体所受的体积力和压力。 若将该微元流体移动d山距离,此距离对x,y,z轴的分量为dx,dy,d止,将上列方程 组分别乘以c,,止并相加可得: 6
西北大学化工原理电子教案 x x p p δ ∂ ∂ ×− 2 1 ,作用于 a’b’c’d’面上的压强为 x x p p δ ∂ ∂ ×+ 2 1 。因此作用于该两表面上的 压力分别为: zyx x p p ⎟ δδδ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ×− 2 1 和 zyx x p p ⎟ δδδ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ×+ 2 1 z y O d’ c’ b’ a’ d c b a A x x x p p δ ∂ ∂ ×− 2 1 x x p p δ ∂ ∂ ×+ 2 1 图 1-6 流体微元的受力平衡 (2) 体积力 设作用于单位质量流体上的体积力在 x 方向的分量为 X,则微元所受的体积力 在 x 方向的分量为 ρδ δ δzyxX (式中ρ为密度)。同理,在 y 及 z 轴上微元所受的体积力分别 为 ρδ δ δzyxY Y 和 ρδ δ δzyxZ 。 该流体处于静止状态,外力之和必等于零。对 x 方向,可写成: 0 2 1 2 1 ⎟ + = ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ⎟ ×+− ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ×− zyxXzyx x p pzyx x p p δδδ δδρδδδδ 各项均除以微元体的流体质量 ρδ δ δzyx 可得: ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎬ ⎫ = ∂ ∂ − = ∂ ∂ − = ∂ ∂ − 0 1 0 1 0 1 z p Z y p Y x p X ρ ρ ρ 同理 (1-6) 此式称为欧拉平衡方程。等式左方为单位质量流体所受的体积力和压力。 若将该微元流体移动 dl 距离,此距离对 x,y,z 轴的分量为 dx,dy,dz,将上列方程 组分别乘以 dx,dy,dz 并相加可得: 6

西北大学化工原理电子教案 吧d+2d+d止 -(Xdx +Ydy+Zd2)=0 (1-7) 表示两种力对微元流体作功之和为零。由于静止流体压强仅与空间位置有关,而与时间 无关,所以,式(1-7)左侧第一项括号内即为压强的全微分dp,于是: d迎=Xdk+Yy+Zt (1-8) 式(1-8)是流体平衡的一般表达式。等式两边分别表示压力和体积力所作的功。 平衡方程在重力场中的应用如流体所受的体积力仅为重力,并取?轴方向与重力方向相 反,则:X=0,Y=0,Z=g。将此代入式(1-8),得: dp+pgdz=0 +在=0 (1-9) 设流体不可压缩,即密度ρ与压强无关,可将上式积分得: 卫+g=常数 (1-10) 对于静止流体中任意两点1和2,如图1-7所示: 1 图1-7重力场中静压强分布 +g=+g (1-11) 0 0 或 P2=P+P8(a1-2)=P1+P8h (1-12) 注意:式(1-10)、(1-11)、(1-12)三式仅适用于在重力场中静止的不可压缩流体
西北大学化工原理电子教案 ( 0 1 =++−⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ ZdzYdyXdxdz z p dy y p dx x p ρ ) (1-7) 表示两种力对微元流体作功之和为零。由于静止流体压强仅与空间位置有关,而与时间 无关,所以,式(1-7)左侧第一项括号内即为压强的全微分 dp,于是: ZdzYdyXdx dp ++= ρ (1-8) 式(1-8)是流体平衡的一般表达式。等式两边分别表示压力和体积力所作的功。 平衡方程在重力场中的应用 如流体所受的体积力仅为重力,并取 z 轴方向与重力方向相 反,则:X=0,Y=0,Z=-g。将此代入式(1-8),得: + ρgdzdp = 0 ∫ ∫ dzg =+ 0 dp ρ (1-9) 设流体不可压缩,即密度ρ与压强无关,可将上式积分得: gz =+ 常数 p ρ (1-10) 对于静止流体中任意两点 1 和 2,如图 1-7 所示: h z1 z2 图 1-7 重力场中静压强分布 2 2 1 1 gz p gz p +=+ ρρ (1-11) = + ρ − = + ρghpzzgpp 12 121 或 )( (1-12) 注意:式(1-10)、(1-11)、(1-12)三式仅适用于在重力场中静止的不可压缩流体。 7

西北大学化工原理电子教案 1.2.2压强能与位能 g项实质上是单位质量流体所具有的位能。P相应地是单位质量流体所具有的压强能。 静止流体存在着两种形式的势能(位能和压强能),在同一种静止流体中处于不同位置的微 元其位能和压强能各不相同,但其和即总势能保持不变。若以符号一 表示单位质量流体 的总势能,则 =g+ (1-13) 式中乎具有与压强相同的因次,可理解为一种虚拟的压强。 乎=Pg+p (1-14) 对不可压缩流体,同种静止流体各点的虚拟压强处处相等。注意:乎的大小与密度有 关,即与流体种类有关。 1.2.3压强的表示方法 压强的其它表示方法压强的大小除直接以P表示外,工程上常间接地以流体柱高度表示, 如用米水柱或毫米汞柱等。液柱高度h与压强的关系为: p=pgh (1-15) 注意:当以液柱高度h表示压强时,必须同时指明为何种流体。 1atm(标准大气压)=1.013×103Pa,相当于760mmHg或10.33mH20。 压强的基准压强的大小常以两种不同的基准来表示:一是绝对真空:二是大气压强。以绝 对真空为基准量得的压强称为绝对压强,以大气压强为基准量得的压强称为表压或真空度。 表压 大气压 绝对压力 真空度 P2 绝对压力 绝对真空 图1-8压强的基准和量度 表压=绝对压一大气压:真空度=大气压一绝对压。 8
西北大学化工原理电子教案 1.2.2 压强能与位能 gz 项实质上是单位质量流体所具有的位能。 ρ p 相应地是单位质量流体所具有的压强能。 静止流体存在着两种形式的势能(位能和压强能),在同一种静止流体中处于不同位置的微 元其位能和压强能各不相同,但其和即总势能保持不变。若以符号 表示单位质量流体 的总势能,则 P ρ (1-13) 式中 P 具有与压强相同的因次,可理解为一种虚拟的压强。 (1-14) 对不可压缩流体,同种静止流体各点 P ρρ p gz += P = ρgz + p 的虚拟压强处处相等。注意:P 的大小与ρ密度有 关,即与流体种类有关。 1.2.3 压强的表示方法 压强的大小除直接以 Pa 表示外,工程上常间接地以流体柱高度表示, (1-15) 注意:当以液柱高度 h 表示压强时, O。 强的基准 压强的大小常以两种不同的基准来表示:一是绝对真空;二是大气压强。以绝 图 1-8 压强的基准和量度 表压 = 绝对压-大气压;真 压强的其它表示方法 如用米水柱或毫米汞柱等。液柱高度 h 与压强的关系为: p = ρgh 必须同时指明为何种流体。 1atm(标准大气压)=1.013×105 Pa,相当于 760mmHg或 10.33mH2 压 对真空为基准量得的压强称为绝对压强,以大气压强为基准量得的压强称为表压或真空度。 空度 = 大气压-绝对压。 绝对真空 p1 大气压 绝对压力 绝对压力 表压 真空度 p2 8

西北大学化工原理电子教案 1.2.4压强的静力学测量方法 压强的测量仪表很多,本节仅介绍应用静力学原理测量压强的方法。 简单测压管。最简单的测压管如图1-9所示。 Pa=pa+Rpg A点的表压为: PA-Pa=Rpg (1-16) 图1-9简单测压管 简单测压管只适用于高于大气压的液体压强的测定,不能适用于气体。此外,如被测压强 P4过大,读数R也将过大,测压很不方便。反之,如被测压强与大气压过于接近,读数R将 很小,使测量误差增大。 U形测压管图1-10表示用U形测压管测量容器中的A点压强。在U形玻璃管内放有某种 液体作为指示液。指示液必须与被测流体不发生化学反应且不互溶,其密度大于被测流体 的密度p 由静力学原理可知,在同一种静止流体内部等高面即是等压面, 即p1=P2 PI=Pa+pghi p2=Pa+pigR 由此可求得A点的压强为 PA Pa+PgR-pghi 图1-10U型测压管 A点的表压为 Pa -Pa PigR -pgh (1-17) 若容器内为气体,则由气柱h造成的静压强可以忽略,得 PA -Pa =PgR (1-18) 此时U形测压管的指示液读数R表示A点压强与大气压之差,读数R即为A点的表压。 U形压差计如U形测压管的两端分别与两个测压口相连,则可以测得两测压点之间的压 差,故称为压差计。图1-11表示U形压差计测量均匀管内作定态流动时A、B两点的压差。 因U形管内的指示液处于静止,故位于同一水平面1、2两点的压强 pI=pa+pgh 与 P2=PB+pg(h2-R)+pgR
西北大学化工原理电子教案 1.2.4 节仅介绍应用静力学原理测量压强的方法。 简单 A 点的表压为: pA − pa = Rρg (1-16) 图 1-9 简单测压管 简单测压管只适用于高于大气压的液体压强的测定,不能适 压强的静力学测量方法 压强的测量仪表很多,本 测压管 最简单的测压管如图 1-9 所示。 pA = pa + Rρg 用于气体。此外,如被测压强 形测压管 图 1-10 表示用U形测压管测量容器中的 A 点压强。在U形玻璃管内放有某种 学原理可知, 在同一种静止流体内部等高面即是等压面, 即p1 p1 = pA + ρgh1 由此可求得 A 点的 ρigR − ρgh1 图 1-10 U型测压管 A点的表压为 (1-18) 此时 U 形测压管的指示液读数 R 表示 形压差计 如 U 形测压管的两端分别与两个测压口相连,则可以测得两测压点之间的压 与 p2 = p pA过大,读数R也将过大,测压很不方便。反之,如被测压强与大气压过于接近,读数R将 很小,使测量误差增大。 U 液体作为指示液。指示液必须与被测流体不发生化学反应且不互溶,其密度ρi大于被测流体 的密度ρ。 由静力 = p2 p2 = pa + ρigR 压强为 pA = pa + pA − pa = ρigR − ρgh1 (1-17) 若容器内为气体,则由气柱h1造成的静压强可以忽略,得 pA − pa = ρigR A 点压强与大气压之差,读数 R 即为 A 点的表压。 U 差,故称为压差计。图 1-11 表示 U 形压差计测量均匀管内作定态流动时 A、B 两点的压差。 因 U 形管内的指示液处于静止,故位于同一水平面 1、2 两点的压强 p1 = pA + ρgh1 BB + ρg(h2 − R) + ρigR 9
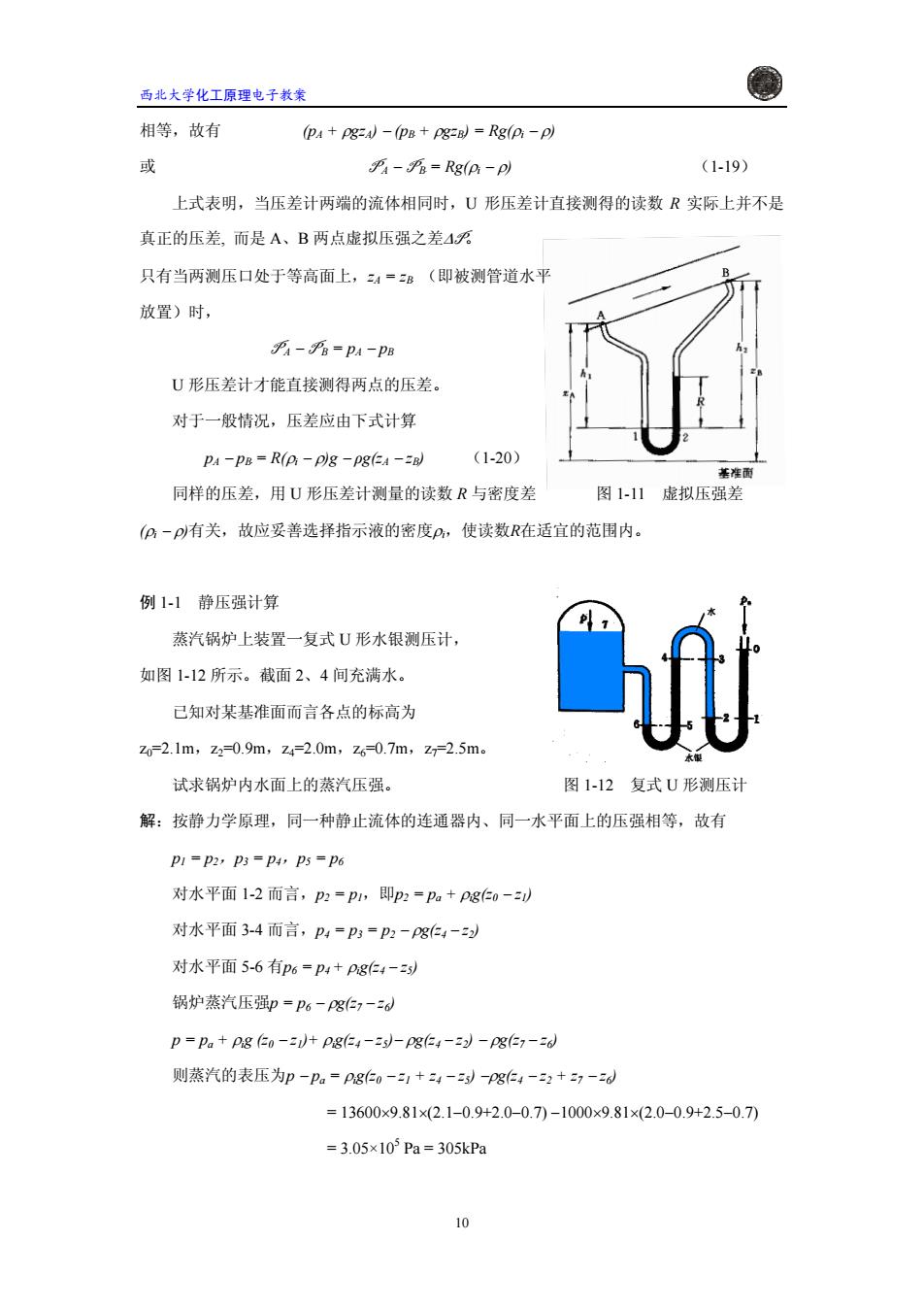
西北大学化工原理电子教案 相等,故有 (PA+P8=A)-(PB+Pg=B)=Rg(p:-p) 或 =Rg(pi-p) (1-19) 上式表明,当压差计两端的流体相同时,U形压差计直接测得的读数R实际上并不是 真正的压差,而是A、B两点虚拟压强之差4万 只有当两测压口处于等高面上,4=B(即被测管道水平 放置)时, 乎A-%=pA-PB U形压差计才能直接测得两点的压差。 对于一般情况,压差应由下式计算 PA-PB=R(Pi-p)g -p8(A-B) (1-20) 基准面 同样的压差,用U形压差计测量的读数R与密度差 图111虚拟压强差 (P一p有关,故应妥善选择指示液的密度P,使读数R在适宜的范围内。 例1-1静压强计算 蒸汽锅炉上装置一复式U形水银测压计, 如图1-12所示。截面2、4间充满水。 己知对某基准面而言各点的标高为 Z0-2.1m,z2=0.9m,Z4=2.0m,z6=0.7m,z斤2.5m。 试求锅炉内水面上的蒸汽压强。 图1-12复式U形测压计 解:按静力学原理,同一种静止流体的连通器内、同一水平面上的压强相等,故有 P1=P2,P3=P4,P5=P6 对水平面1-2而言,p2=p,即p2=Pa+P8仁0-) 对水平面3-4而言,P4=P3=p2-Pg4-) 对水平面5-6有p6=p4+P8e4-到 锅炉蒸汽压强p=P6-Pg仁1-6d p=Pa+pg (o-1)+P8(4-Es)-p8(E4-22)-pg(=7-36) 则蒸汽的表压为p-pa=P80-1+24-)-Pg4-2+27-d =13600×9.81×(2.1-0.9+2.0-0.7)-1000×9.81×(2.0-0.9+2.5-0.7) =3.05×105Pa=305kPa 10
西北大学化工原理电子教案 相等,故有 (pA + ρgzA) − (pB + B ρgzBB) = Rg(ρ − ρ) i 或 P A − P B = Rg( B ρ (1-19) 是 真正 − ρ) i 上式表明,当压差计两端的流体相同时,U 形压差计直接测得的读数 R 实际上并不 的压差, 而是 A、B 两点虚拟压强之差ΔP。 只有当两测压口处于等高面上,zA = zBB (即被测管道水平 P A − P B = pA − pB U 形压差计才能直接测得两点的压差。 放置)时, 对于一般情况,压差应由下式计算 pA − pB = R( B ρi − ρ)g − ρg(zA − zBB (1-20) 同样 R 图 1-11 虚拟压强差 (ρi − 1-1 静压强计算 一复式 U 形水银测压计, 如图 z0=2 z7=2.5m。 图 1-12 复式 U 形测压计 解: p1,即p2 = pa + ρig(z0 − z1) ρg(z4 − z2) − ρg(z7 − z6) z7 − z6) ×(2.0−0.9+2.5−0.7) ) 的压差,用 U 形压差计测量的读数 与密度差 ρ)有关,故应妥善选择指示液的密度ρi,使读数R在适宜的范围内。 例 蒸汽锅炉上装置 1-12 所示。截面 2、4 间充满水。 已知对某基准面而言各点的标高为 .1m,z2=0.9m,z4=2.0m,z6=0.7m, 试求锅炉内水面上的蒸汽压强。 按静力学原理,同一种静止流体的连通器内、同一水平面上的压强相等,故有 p1 = p2,p3 = p4,p5 = p6 对水平面 1-2 而言,p2 = 对水平面 3-4 而言,p4 = p3 = p2 − ρg(z4 − z2) 对水平面 5-6 有p6 = p4 + ρig(z4 − z5) 锅炉蒸汽压强p = p6 − ρg(z7 − z6) p = pa + ρig (z0 − z1)+ ρig(z4 − z5)− 则蒸汽的表压为p − pa = ρig(z0 − z1 + z4 − z5) −ρg(z4 − z2 + = 13600×9.81×(2.1−0.9+2.0−0.7) −1000×9.81 = 3.05×105 Pa = 305kPa 10