
第5节 第七章 方向导数与梯度 一、方向导数 二、梯度 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页 返回 结束
目录 上页 下页 返回 结束 第七章 第5节 一、方向导数 二、梯度 方向导数与梯度

一、方向导数 定义1若函数f(x,y)在点P(x,y)处 沿方向1(方向角为α,B)存在下列极限: P(x,y) lim △f x p>0 0 lim f(x+△x,y+△y)-f(x,y)记作∂f p-→0 al 】 则称⊙f 为函数在点P处沿方向1的方向导数 al BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束
目录 上页 下页 返回 结束 一、方向导数 定义1 若函数 f (x, y) f 0 lim 则称 l f l f ( ) ( ) , 2 2 x y x cos , y cos 为函数在点 P 处沿方向 l 的方向导数. ( , ) ( , ) lim 0 f x x y y f x y 在点P(x, y) 处 沿方向 l (方向角为 , ) 存在下列极限: 记作 P(x, y) l x y O ' P

定理若函数f(x,y)在点P(x,y)处可微, 则函数在该点沿任一方向1的方向导数存在,且有 B1=Ofcosa+ fcosB. 其中a,B为l的方向角 P(x,y) 证明:由函数f(x,y)在点P可微,得 Aj=IAx+I△ytop) 8x 0y =p(wa一影as))-olp) 故 of lim Af =2f cosa+ of cosB al p-→0 8x BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束
目录 上页 下页 返回 结束 定理 若函数 f (x, y) 在点 P(x, y) 处可微 , 则函数在该点沿任一方向 l 的方向导数存在 , f l f 0 lim cos cos , y f x f l f 其中 , 为l的方向角. 证明: 由函数 f (x, y) y o ( ) y f x x f f cos cos y f x f 且有 o( ) 在点 P 可微 , 得 故 cos cos y f x f P(x, y) l x y O ' P

特别: ·当/与x轴同向a=0,B=)时,有 of af al 8x ·当1与x轴反向(a=不,B=乃时,有 of of al 8x 对于三元函数f(x,y,)在点P(x,y,z)处可微分,则 of lim f(x+△x,y+△y,2+△)-f(x,y,2) al p→0 of osa+0Lcosg+ cos y x 0y 0z P=(A)2+(A)2+(A=2, Ax=pcosa,△y=PcoS阝,A2=pcosy BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 上页 下页 返回 结束
目录 上页 下页 返回 结束 x f l f 特别: • 当 l 与 x 轴同向 时,有 2 0, α β • 当 l 与 x 轴反向 时,有 2 , α β x f l f 对于三元函数 f (x, y,z) 在点 P(x, y,z) 处可微分,则 ( , , ) ( , , ) lim 0 f x x y y z z f x y z l f cos cos cos z f y f x f ( ) ( ) ( ) , 2 2 2 x y z x cos , y cos , z cos

例7.5.1求函数z=x2+y在点2,1)处沿方向1=37-47 的方向导数 解:向量1的方向余弦为 3 4 cosa= 5 cosA=- 5 =2x =4, =2y =2, @x (2,1 (2,1) y2, (2,1) 故在点(2,1)处,所求方向导数 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页返回 结束
目录 上页 下页 返回 结束 例7.5.1 求函数z x 2 y 2在点 (2, 1) 处沿方向l 3i 4 j 的方向导数 . , 5 3 cos 2 4, (2,1) (2,1) x x z , 5 4 cos 解: 向量 l 的方向余弦为 2 2, (2,1) (2,1) y y z 故在点 (2, 1) 处,所求方向导数 . 5 4 5 4 2 5 3 4 l z

二、梯度 定义2设函数z=x,y)在点x,y)的某邻域内具 有一阶连续偏导数 1⊙,则向量 Ox oy 8I+ ∂x 称为函数z=x,y)在点(x,y)的梯度,记作gradfx, ),即 gradf() 影 0x BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页返回 结束
目录 上页 下页 返回 结束 二、梯度 定义2 设函数z=f(x,y)在点(x,y)的某邻域内具 有一阶连续偏导数 ,则向量 y f x f , j y f i x f 称为函数z=f(x,y)在点(x,y)的梯度,记作gradf(x, y),即 j y f i x f f x y grad ( , )

(1)当0=0时, 达到最大,最大值是 gradf(x,y) 即方向与梯度的方向一致时,方向导数取到最大 值.梯度的方向是函数x,y)在点(x,y)增长最快 的方向 (2)当0=π时, 亲到最小,最小值是 -gradf(x,y). 即负梯度的方向是函数x,y)在点(x,y)减少最快 的方向 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束
目录 上页 下页 返回 结束 (1)当θ=0时, 达到最大,最大值是 | ( , ) | . 2 2 y f x f gradf x y | gradf (x, y) | . l f 即方向l与梯度的方向一致时,方向导数取到最大 值.梯度的方向是函数f(x,y)在点(x,y)增长最快 的方向. (2)当θ=π时, 达到最小,最小值是 l f 即负梯度的方向是函数f(x,y)在点(x,y)减少最快 的方向.

梯度的几何意义 对函数:=f(x,),曲线 任》在0面1的设影 D:f(x,y)=c称为函数f的等值线或等高线.举例 设fx,才,不同时为零, 则L*上点P处的法向量为 (fs,fy)p=gradf p =Vfp 函数在一点的梯度垂直于该点等值线! 指向函数增大的方向 同样,f(x,y,z)=c称为u=f(x,y,z) 的等值面(等量面).当其各偏导数不同 (设c,<C2) 时为零时,其上点P处的法向量为gradfp=Vfp BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束
目录 上页 下页 返回 结束 梯度的几何意义 O y x 1 f c f c ( ) 1 2 设c c P 曲线 在 xOy 面上的投影 z c z f x y ( , ) L : f (x, y) c * 称为函数 f 的等值线或等高线 . 设 , 不同时为零 , x y f f 则L*上点P 处的法向量为 x y P ( f , f ) P grad f 2 f c 对函数 z f (x, y), 举例 函数在一点的梯度垂直于该点等值线, 指向函数增大的方向. 同样, u f (x, y,z) 的等值面(等量面). f (x, y,z) c 当其各偏导数不同 其上点 P 处的法向量为 P grad f 称为 时为零时, P f . P f
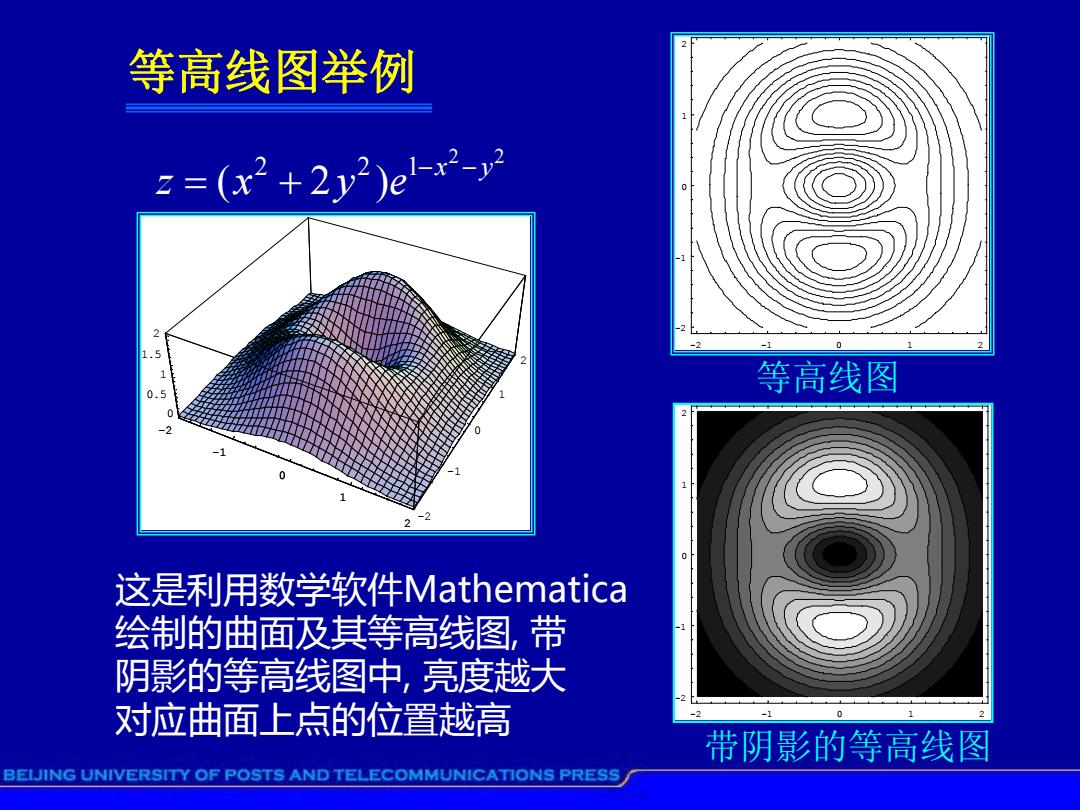
等高线图举例 2=(x2+2y2)e-2-y 等高线图 这是利用数学软件Mathematica 急 绘制的曲面及其等高线图,带 阴影的等高线图中,亮度越大 -2 对应曲面上点的位置越高 -2 2 带阴影的等高线图 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS
等高线图举例 -2 -1 0 1 2 -2 -1 0 1 2 0 0.5 1 1.5 2 -2 -1 0 1 2 -2 -1 0 1 2 -2 -1 0 1 2 2 2 2 2 1 ( 2 ) x y z x y e -2 -1 0 1 2 -2 -1 0 1 2 这是利用数学软件Mathematica 绘制的曲面及其等高线图, 带 阴影的等高线图中, 亮度越大 对应曲面上点的位置越高 等高线图 带阴影的等高线图

例7.5.3求梯度向量grad x2+y2 解自于x刀求架 2x of 2y ax (x2+y>(x2+y2 grad 2× 2y BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页返回 结束
目录 上页 下页 返回 结束 例7.5.3 求梯度向量 解: 由于 , ( ) 2 , ( ) 2 2 2 2 2 2 2 x y y y f x y x x f . 1 2 2 x y grad ,求得 1 ( , ) 2 2 x y f x y . ( ) 2 ( ) 1 2 2 2 2 2 2 2 2 2 j x y y i x y x x y grad