
8寡头垄断企业的竞争行为 对寡头垄断企业市场竞争行为的分析是博弈论在经济学中的重要应用.早在博弈论产生 之前,有的经济学家就已运用博弈论的思想,分析寡头垄断企业的市场竞争行为,并建立起 相应的竞争模型。随若博弈论的产生及其在产业经济学中的应用,有关寡头垄断企业竞争的 博弈分析大量出现。本章主要运用博弈论的思想和表达方式,按照静态竞争、动态竞争的顺 序,对寡头垄断企业的主要竞争模型进行介绍和分析,并揭示其经济学含义。最后,对寡头 垄断市场上的企业合谋与卡特尔行为的产生动因和影响因素进行分析。 8.1寡头垄断企业的静态竞争及其博弈模型 寡头垄断企业的静态竞争及其博弈原理 从理论上讲,市场结构可以划分为四种不同的形态:完全竞争市场、完全垄断市场、垄 断竞争市场和寡头垄断市场,前三种市场结构下的企业竞争主要考虑企业自身的约束条件, 并且在传统经济学教科书里都有相对固定的分析模型和相应的短期和长期均衡条件.在寡头 座断市场上,真头断企业之间在产:量和价格的制定上相互影响、相互制约,企业竞争行为 和战略的选择,不仅考虑自身的影响因素,也要考虑对竞争对手的影响以及可能引起的反应 而寡头垄断市场的这种特点决定了博弈论在研究寡头垄断企业竞争行为中的重要的应用色 值。 博弈论(Game Theory)是研究行为决策主体的行为发生直接相互作用时的决策,以及 这种决策的均衡问题的经济学分支,也就是说,当一个行为主体的选择受到其他行为主体选 择影向,而日反过来影响到盐他行为主休洗择时的决笛问顾和的衡问顺。在博弈过程中,行 为主体决策的效用函数 不仅依赖于他自己的 择,而且依赖于与其具有博奔关系的其他行为 方的选择:个人的最优选择及其得益是其他人选择的函数。根据上述分析,寡头垄断企业的 竞争行为与博弈论关于竞争主体的行为假定是一致的,由此决定了寡头坐断企业的竞争行为 成为博弈论原理的重要应用领域,可以说所有的寡头垄断竞争模型都是博弈论有关原理的具 体应用。 尽管寡头垄断市场上的企业竞争充满了不确定性,竞争双方的成略选择相互影响,但对 这些行为的分析仍然可以在一定的假设条件下进行分析。从竞争行为的时序性划分,可分 静态竞争与动态竞争。关于寡头垄断企业竞争的早期研究主要集中于其静态的或单时期的市 场竞争模型,这些模型适用于仅持续一个较短期限的市场,作为竞争对手的厂商是同时作出 决策并只竞争一次。在这种情况下,即使各厂商对被此可能有的产量、价格等策略以及其对 各自的影响是完全清楚的,但由于只进行一次性竞争,所以彼此之间仍然没有机会事先观察 竞争对手的行动 人而选择相应的决策 所以 每个厂商在这种市场上是 时作出决策,而 且这种决策在其后相当长的一段时间内不会重新出现,或者说其下一次出现的概率近乎于 零。在博弈论上,对于这样一种竞争行为主要是用完全信息的静态博奔来分析的。静态博奔 是指在博弈中,参与人同时选择行动,或虽非同时但后行动者并不知道前行动者采取了什么 见体行动。完全信息则是指每一个参与人对所有其他参与人的特征、战略空间及其支付函数 都具有准确的信息。完全信息静态博奔是博弈论中最基本的 一种博奔形式,其所对应的均衡 概念是纳什均衡。纳什均衡是指假设有个博弈方参与博弈,给定其他人策略的条件下,每 个人选择自己的最优策略,所有参与人的最优策略一起构成的一个策略组合即为纳什均衡。 在纳什均衡状态,给定其他参与人策略不变的情况下,没有任何单个参与人有动机选择其他
8 寡头垄断企业的竞争行为 对寡头垄断企业市场竞争行为的分析是博弈论在经济学中的重要应用。早在博弈论产生 之前,有的经济学家就已运用博弈论的思想,分析寡头垄断企业的市场竞争行为,并建立起 相应的竞争模型。随着博弈论的产生及其在产业经济学中的应用,有关寡头垄断企业竞争的 博弈分析大量出现。本章主要运用博弈论的思想和表达方式,按照静态竞争、动态竞争的顺 序,对寡头垄断企业的主要竞争模型进行介绍和分析,并揭示其经济学含义。最后,对寡头 垄断市场上的企业合谋与卡特尔行为的产生动因和影响因素进行分析。 8.1 寡头垄断企业的静态竞争及其博弈模型 寡头垄断企业的静态竞争及其博弈原理 从理论上讲,市场结构可以划分为四种不同的形态:完全竞争市场、完全垄断市场、垄 断竞争市场和寡头垄断市场。前三种市场结构下的企业竞争主要考虑企业自身的约束条件, 并且在传统经济学教科书里都有相对固定的分析模型和相应的短期和长期均衡条件。在寡头 垄断市场上,寡头垄断企业之间在产量和价格的制定上相互影响、相互制约,企业竞争行为 和战略的选择,不仅考虑自身的影响因素,也要考虑对竞争对手的影响以及可能引起的反应。 而寡头垄断市场的这种特点决定了博弈论在研究寡头垄断企业竞争行为中的重要的应用价 值。 博弈论(Game Theory)是研究行为决策主体的行为发生直接相互作用时的决策,以及 这种决策的均衡问题的经济学分支,也就是说,当一个行为主体的选择受到其他行为主体选 择影响,而且反过来影响到其他行为主体选择时的决策问题和均衡问题。在博弈过程中,行 为主体决策的效用函数不仅依赖于他自己的选择,而且依赖于与其具有博弈关系的其他行为 方的选择:个人的最优选择及其得益是其他人选择的函数。根据上述分析,寡头垄断企业的 竞争行为与博弈论关于竞争主体的行为假定是一致的,由此决定了寡头垄断企业的竞争行为 成为博弈论原理的重要应用领域,可以说所有的寡头垄断竞争模型都是博弈论有关原理的具 体应用。 尽管寡头垄断市场上的企业竞争充满了不确定性,竞争双方的战略选择相互影响,但对 这些行为的分析仍然可以在一定的假设条件下进行分析。从竞争行为的时序性划分,可分为 静态竞争与动态竞争。关于寡头垄断企业竞争的早期研究主要集中于其静态的或单时期的市 场竞争模型,这些模型适用于仅持续一个较短期限的市场,作为竞争对手的厂商是同时作出 决策并只竞争一次。在这种情况下,即使各厂商对彼此可能有的产量、价格等策略以及其对 各自的影响是完全清楚的,但由于只进行一次性竞争,所以彼此之间仍然没有机会事先观察 竞争对手的行动,从而选择相应的决策。所以,每个厂商在这种市场上是同时作出决策,而 且这种决策在其后相当长的一段时间内不会重新出现,或者说其下一次出现的概率近乎于 零。在博弈论上,对于这样一种竞争行为主要是用完全信息的静态博弈来分析的。静态博弈 是指在博弈中,参与人同时选择行动,或虽非同时但后行动者并不知道前行动者采取了什么 具体行动。完全信息则是指每一个参与人对所有其他参与人的特征、战略空间及其支付函数 都具有准确的信息。完全信息静态博弈是博弈论中最基本的一种博弈形式,其所对应的均衡 概念是纳什均衡。纳什均衡是指假设有n 个博弈方参与博弈,给定其他人策略的条件下,每 个人选择自己的最优策略,所有参与人的最优策略一起构成的一个策略组合即为纳什均衡。 在纳什均衡状态,给定其他参与人策略不变的情况下,没有任何单个参与人有动机选择其他

策略,从而没有任何人有积极性打破这种均衡。本节将要介绍的古诺产量竞争模型、伯特兰 德价格竞争模型和豪泰林产品决策模型都是完全信息静态博奔的经典模型。 古诺(Cournot)产量竞争模型 双寡头古诺竞争模型法国经济学家奥古斯丁·古诺于1838年首次提出了双寡头进行 产量竞争的静态博弈模型,这实际上是以后纳什均衡思想的最早阐述。这一模型是用博奔论 研究产业组织理论的重诬基础,其后这一模型被扩展到对多个寡占厂商行为的研究 在古诺模型中,关于两个寡头的行为及其有关条件的假定是:①两个寡头厂商生产的产 品是同质或无差别的:②每个厂商都根据对手的策略采取行动, 并假定对手会继续这样做 据此来做出自己的决策:③为方使起见,假定每个厂商的边际成本为常数,并假设每个厂商 的需求函数是线形的:④两个厂商都通过调整产量来实现各自利润的最大化:⑤两个厂商不 存在任何正式的或非正式的串谋行为。 下面对古诺模型进行博弈分析。设,、q2分别表示企业1和企业2生产的同质产品的 产量,市场中该产品的总供给Q=q,+q2,令P(Q)=a-Q表示市场出清时的价格(更精 确地表述为:Qa时,P(Q)=0)。 设企业i生产q,的总成本C,(q,)=cg,即企业不存在固定成木,且生产每单位产品的 边际成本为常数c(这里假定c<a)。根据古诺的假定,两个企业同时进行产量决策。假定 产品是连续可分制的,由于产出不可能为负,因此,每一企业的战略空间可表示为 S,=[0,∞,其中一个代表性战略s,就是企业选择的产量q,(q,≥0)。假定企业的收益是 其利润额π,用山,(S,S,)表示,则 π,(q,9)=qpq+q)-c=q.[a-(g,+q)-c] (8.1) 若一对战略(3,3)是纳什均衡,则对每个参与者1,,应满足 4,(s,5)24,(3,5) (8.2) (82)式对S,中每一个可选战略S,都成立。在古诺的双头垄断模型中,上面的条件可 具体表述为:若一对产出组合(q,92)为纳什均衡,则对每一个企业1,9,应为下面最大 化问题的解: maπ,(9,4,)=四ax9.a-(4,+4,)-c 设q,”<a-c,企业i最优化问题的一阶条件为 9.=2(a-9,-c) 也即是,若产量组合(q:',42)为纳什均衡,则企业的产量选择必须满足:
策略,从而没有任何人有积极性打破这种均衡。本节将要介绍的古诺产量竞争模型、伯特兰 德价格竞争模型和豪泰林产品决策模型都是完全信息静态博弈的经典模型。 古诺(Cournot)产量竞争模型 双寡头古诺竞争模型 法国经济学家奥古斯丁·古诺于 1838 年首次提出了双寡头进行 产量竞争的静态博弈模型,这实际上是以后纳什均衡思想的最早阐述。这一模型是用博弈论 研究产业组织理论的重要基础,其后这一模型被扩展到对多个寡占厂商行为的研究。 在古诺模型中,关于两个寡头的行为及其有关条件的假定是:①两个寡头厂商生产的产 品是同质或无差别的;②每个厂商都根据对手的策略采取行动,并假定对手会继续这样做, 据此来做出自己的决策;③为方便起见,假定每个厂商的边际成本为常数,并假设每个厂商 的需求函数是线形的;④两个厂商都通过调整产量来实现各自利润的最大化;⑤两个厂商不 存在任何正式的或非正式的串谋行为。 下面对古诺模型进行博弈分析。设q1、q2 分别表示企业 1 和企业 2 生产的同质产品的 产量,市场中该产品的总供给Qq q 1 2 ,令 P(Q) a Q 表示市场出清时的价格(更精 确地表述为:Q a 时, P( ) Q aQ ,Q a 时, P( ) Q 0)。 设企业i 生产qi 的总成本C q cq ii i ( ) ,即企业不存在固定成本,且生产每单位产品的 边际成本为常数c(这里假定c a )。根据古诺的假定,两个企业同时进行产量决策。假定 产品是连续可分割的,由于产出不可能为负,因此,每一企业的战略空间可表示为 Si 0, ,其中一个代表性战略 i s 就是企业选择的产量 qi (qi 0)。假定企业的收益是 其利润额 ,用 ( , ) i i j u s s 表示,则 ii j i i j i i j ( , ) [( ) ] [ ( ) ] q q q pq q c q a q q c (8.1) 若一对战略( i j s ,s )是纳什均衡,则对每个参与者i , i s 应满足 ( , ) ( , ) i i j i i j u s s u s s (8.2) (8.2)式对 i s 中每一个可选战略 si 都成立。在古诺的双头垄断模型中,上面的条件可 具体表述为:若一对产出组合(, ) q q 1 2 为纳什均衡,则对每一个企业i ,qi 应为下面最大 化问题的解: max ( , ) max [ ( ) ] 0 0 q ii j q i ij i i qq qa q q c 设q ac j ,企业i 最优化问题的一阶条件为: q aq c i j 1 2 ( ) 也即是,若产量组合(, ) q q 1 2 为纳什均衡,则企业的产量选择必须满足:

g=3a-g:-o) (83) 94.=)a-g-c) (84) 联立以上两式,解得q=9:=0 3 下面用反应函数或反应曲线来说明纳什均衡时的产量。 等式9,=(a-q,-c)给出的是针对企业j的均衡战略s,时企业i的最优反应,同 样的方法可以推导出针对企业1的一个任意战略企业2的最优反应,以及针对企业2的任 意一个战略企业1的最优反应。假定企业1的战略q,满足q,<a-c,企业2的最优反应为 R(q)=2(a-g1-c) (85) 类似地,如果q2<a-c,则企业1的最优反应为: R(g)=a-4:-d (8.6) 以上两式分别是企业2对企业1产量q,的反应函数和企业1对企业2产量q2的反应函 数。在这里,反应函数表示的是每个企业的最优战略(产量)是另一个企业产量的函数。由 于这两个函数都是连续的线形函数,因此可用坐标平面上的两条直线表示(见图8-1)。这 两个最优反应函数表示的曲线为反应曲线。两条反应曲线只有一个交点,其交点就是纳什均 衡时两个企业的产量组合」 以上假定两个企业不存在任何形式的串谋。现在假定市场上的两个寡头垄断企业通过串 谋如同一个垄断者一样行事,使两企业总的利润最大化。这时,两企业的产量之和q,+92应 等于垄断产量qm(如g,=q42=qm/2)。可以计算,垄断企业的最优产量为 4-(a-c) 市场垄断利润为x”=口-© 4 两个企业平分垄断利润: π,"=,"=a-c2 8 而古诺均衡时的企业利润水平为: 4,9)=元g,9)=a-c 9 下面通过图8一1比较古诺均衡、竞争均衡和企业串谋情况下的产量、价格和利润水平
( ) 2 1 1 2 q a q c (8.3) ( ) 2 1 2 1 q a q c (8.4) 联立以上两式,解得q q a c 1 2 3 下面用反应函数或反应曲线来说明纳什均衡时的产量。 等式 ( ) 2 1 q a q c i j 给出的是针对企业 j 的均衡战略 sj 时企业i 的最优反应,同 样的方法可以推导出针对企业 1 的一个任意战略企业 2 的最优反应,以及针对企业 2 的任 意一个战略企业 1 的最优反应。假定企业 1 的战略q1满足 q a c 1 ,企业 2 的最优反应为 Rq a q c 21 1 1 2 () ( ) (8.5) 类似地,如果 q a c 2 ,则企业 1 的最优反应为: Rq a q c 12 2 1 2 () ( ) (8.6) 以上两式分别是企业 2 对企业 1 产量q1的反应函数和企业 1 对企业 2 产量q2 的反应函 数。在这里,反应函数表示的是每个企业的最优战略(产量)是另一个企业产量的函数。由 于这两个函数都是连续的线形函数,因此可用坐标平面上的两条直线表示(见图 8-1)。这 两个最优反应函数表示的曲线为反应曲线。两条反应曲线只有一个交点,其交点就是纳什均 衡时两个企业的产量组合。 以上假定两个企业不存在任何形式的串谋。现在假定市场上的两个寡头垄断企业通过串 谋如同一个垄断者一样行事,使两企业总的利润最大化。这时,两企业的产量之和q1 + q2 应 等于垄断产量qm (如 q1 q2 qm / 2 )。可以计算,垄断企业的最优产量为 q ac m 1 2 ( ) 市场垄断利润为 m a c ( ) 2 4 两个企业平分垄断利润: 1 2 2 8 m m a c ( ) 而古诺均衡时的企业利润水平为: 9 ( ) ( , ) ( , ) 2 1 1 2 2 1 2 a c q q q q 下面通过图 8—1 比较古诺均衡、竞争均衡和企业串谋情况下的产量、价格和利润水平
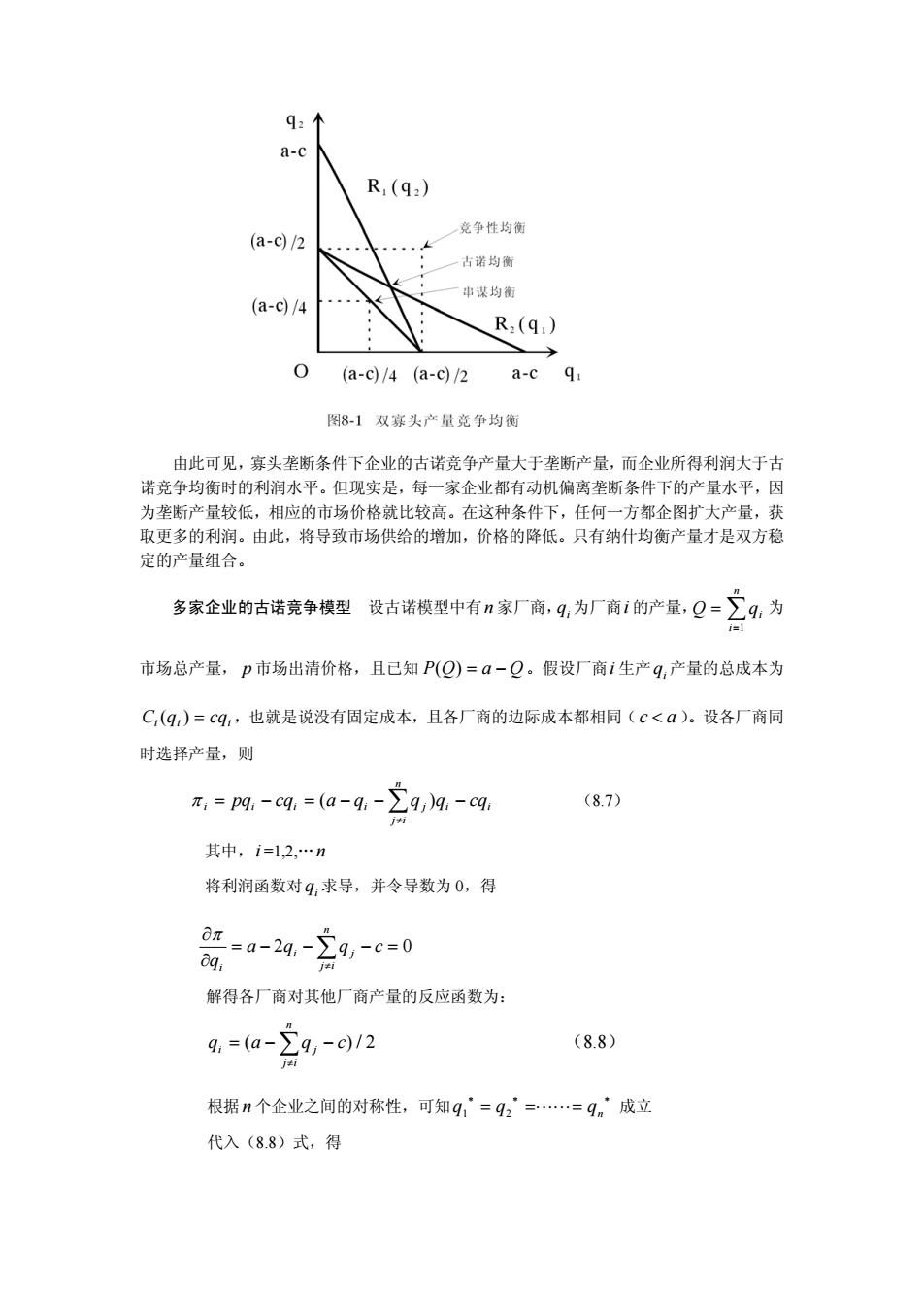
q:个 a-c R(9) (a-c)/2 竞争性均衡 古送均衡 (a-c/4 R,(9) 0 (a-c)/4(a-c)/2 a-c qi 图81双寡头产量竞争均衡 由此可见,寡头垄断条件下企业的古诺竞争产量大于垄断产量,而企业所得利润大于古 诺竞争均衡时的利润水平。但现实是,每一家企业都有动机偏离垄断条件下的产量水平,因 为垄断产量较低,相应的市场价格就比较高。在这种条件下,任何一方都企图扩大产量,获 取更多的利润。由此,将导致市场供给的增加,价格的降低。只有纳什均衡产量才是双方稳 定的产量组合 多家企业的古诺竞争模型设古诺模型中有n家厂商,9,为厂商的产量,Q=∑g,为 市场总产量,p市场出清价格,且已知P(Q)=a-Q。假设厂商1生产q,产量的总成本为 C,(q,)=cg,也就是说没有固定成本,且各厂商的边际成本都相同(c<a)。设各厂商同 时选择产量,则 ,=pm,-cg,=(a-9-∑9,9,-c (8.7) 其中,i=1,2,…n 将利润函数对4,求导,并令导数为0,得 00-24-29,-0=0 解得各厂商对其他厂商产量的反应函数为: q,=(a-∑9,-c)/2 (8.8) 根据n个企业之间的对称性,可知q,”=92”==gm‘成立 代入(8.8)式,得
由此可见,寡头垄断条件下企业的古诺竞争产量大于垄断产量,而企业所得利润大于古 诺竞争均衡时的利润水平。但现实是,每一家企业都有动机偏离垄断条件下的产量水平,因 为垄断产量较低,相应的市场价格就比较高。在这种条件下,任何一方都企图扩大产量,获 取更多的利润。由此,将导致市场供给的增加,价格的降低。只有纳什均衡产量才是双方稳 定的产量组合。 多家企业的古诺竞争模型 设古诺模型中有n 家厂商,qi 为厂商i 的产量,Q qi i n 1 为 市场总产量, p 市场出清价格,且已知 P( ) Q a Q。假设厂商i 生产qi 产量的总成本为 C q cq ii i ( ) ,也就是说没有固定成本,且各厂商的边际成本都相同(c a )。设各厂商同 时选择产量,则 i ii i j j i n pq cq a q q q cq i i ( ) (8.7) 其中,i =1,2,…n 将利润函数对qi 求导,并令导数为 0,得 n j i i j i a q q c q 2 0 解得各厂商对其他厂商产量的反应函数为: q a qc i j j i n ( )/2 (8.8) 根据n 个企业之间的对称性,可知qq q 1 2 n 成立 代入(8.8)式,得

gi=9g- 行业总产量为: a,'-na-o n+1 市场价格为: p=a- n(a-c)a+nc n+1n+1 每个金业的利涧:元,=(p-c9,广=a-a9-d小二=a- n+1 n+1(n+)2 需注意的是,在古诺均衡时,价格高出边际成本的幅度为: p-c=a-na-o)-c= -c n+1 *0 显然,Iim(p-c)=0 这说明,当企业个数无穷多时,产出和价格均趋于完全竞争条件下的均衡水平,市场结 构会趋于完全竞争市场:当=1时,该市场即为完全垄断市场,厂商所提供的产量只是完 全竞争市场的12,而价格则比完全竞争价格高出(a-c)/2,这意味者完全垄断厂商将比竞 垄断要低(a-c)/6. 通过以上分析可知,在一个产业中,如果新企业不断进入,市场产量将会不断增加,而 价格将会下降,从而有助于增加消费者的福利。当新进入企业数量增加到一定程度,市场结 构将趋近完全竞争状态。这说明,通过降低产业进入壁垒或放松进入管制,使潜在进入企业 能够顺利进入行业,并对产业中原有企业的市场地位形成一种威胁,就能够降低产业市场价 格,增加产量,提高资源配置效率
qq q 1 2 n = a c n 1 行业总产量为: q na c n j j n ( ) 1 1 市场价格为: 1 1 ( ) n a nc n n a c p a 每个企业的利润: 2 2 ( 1) ( ) 1 ] 1 ( ) ( ) [ n a c n a c c n n a c j p c q j a 需注意的是,在古诺均衡时,价格高出边际成本的幅度为: pc a na c n c a c n ( ) 1 1 0 显然, lim( ) n p c 0 这说明,当企业个数无穷多时,产出和价格均趋于完全竞争条件下的均衡水平,市场结 构会趋于完全竞争市场;当 n=1 时,该市场即为完全垄断市场,厂商所提供的产量只是完 全竞争市场的 1/2,而价格则比完全竞争价格高出( ) a c /2,这意味着完全垄断厂商将比竞 争厂商获取更高的利润;而当 n=2 时,即为古诺揭示的双边寡头垄断模型,两个寡头厂商 所提供的市场产量只是完全竞争市场的 2/3,价格比完全竞争价格高出( ) a c /3,但比完全 垄断要低( ) a c /6。 通过以上分析可知,在一个产业中,如果新企业不断进入,市场产量将会不断增加,而 价格将会下降,从而有助于增加消费者的福利。当新进入企业数量增加到一定程度,市场结 构将趋近完全竞争状态。这说明,通过降低产业进入壁垒或放松进入管制,使潜在进入企业 能够顺利进入行业,并对产业中原有企业的市场地位形成一种威胁,就能够降低产业市场价 格,增加产量,提高资源配置效率