
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 1 第四章 化学反应速率与反应动 力学初步 Chapter 4 Primary Conception of Chemical Reaction Rate & Reaction Kinetics 教学要求 1. 初步了解化学反应速率、速率方程、碰撞理论、过渡状态理论和活化能概念; 2.理解并会用浓度、温度、催化剂诸因素解释其对化学反应速率的影响; 3.初步掌握阿仑尼乌斯公式的应用,会用其求算活化能及某温度下的反应速率; 4.理解反应分子数和反应级数的概念,会进行基元反应有关的简单计算; 5.初步掌握零级、一级和二级反应的特征。 课时分配(6 学时) 1.化学反应速率的表示方法 2.反应速率理论简介 碰撞理论 过渡状态理论 ( 以上共 2 学时 ) 3.活化能 4.影响化学反应速率的因素(浓度、温度、反应物接触状况、催化剂) 5.化学反应机理 反应分子数和反应级数 一级、二级、零级反应的特征 反应机理研究方法 ( 以上共 4 学时 ) 前言 化学反应是用化学方程式表示的,尽管它能规范又简练地表明反应物、产物及它们相互 转化的数量关系,但实质性的许多问题却不能解决: 1.给定条件下反应自发进行的趋势(过程的判据) 2.转化程度(反应程度) 这两个问题反应在能量上,属化学热力学概念。 3.反应进行的速率(快慢) 4.反应历程,即中间步骤(反应机理) 后两个问题属化学反应动力学范畴
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 1 第四章 化学反应速率与反应动 力学初步 Chapter 4 Primary Conception of Chemical Reaction Rate & Reaction Kinetics 教学要求 1. 初步了解化学反应速率、速率方程、碰撞理论、过渡状态理论和活化能概念; 2.理解并会用浓度、温度、催化剂诸因素解释其对化学反应速率的影响; 3.初步掌握阿仑尼乌斯公式的应用,会用其求算活化能及某温度下的反应速率; 4.理解反应分子数和反应级数的概念,会进行基元反应有关的简单计算; 5.初步掌握零级、一级和二级反应的特征。 课时分配(6 学时) 1.化学反应速率的表示方法 2.反应速率理论简介 碰撞理论 过渡状态理论 ( 以上共 2 学时 ) 3.活化能 4.影响化学反应速率的因素(浓度、温度、反应物接触状况、催化剂) 5.化学反应机理 反应分子数和反应级数 一级、二级、零级反应的特征 反应机理研究方法 ( 以上共 4 学时 ) 前言 化学反应是用化学方程式表示的,尽管它能规范又简练地表明反应物、产物及它们相互 转化的数量关系,但实质性的许多问题却不能解决: 1.给定条件下反应自发进行的趋势(过程的判据) 2.转化程度(反应程度) 这两个问题反应在能量上,属化学热力学概念。 3.反应进行的速率(快慢) 4.反应历程,即中间步骤(反应机理) 后两个问题属化学反应动力学范畴
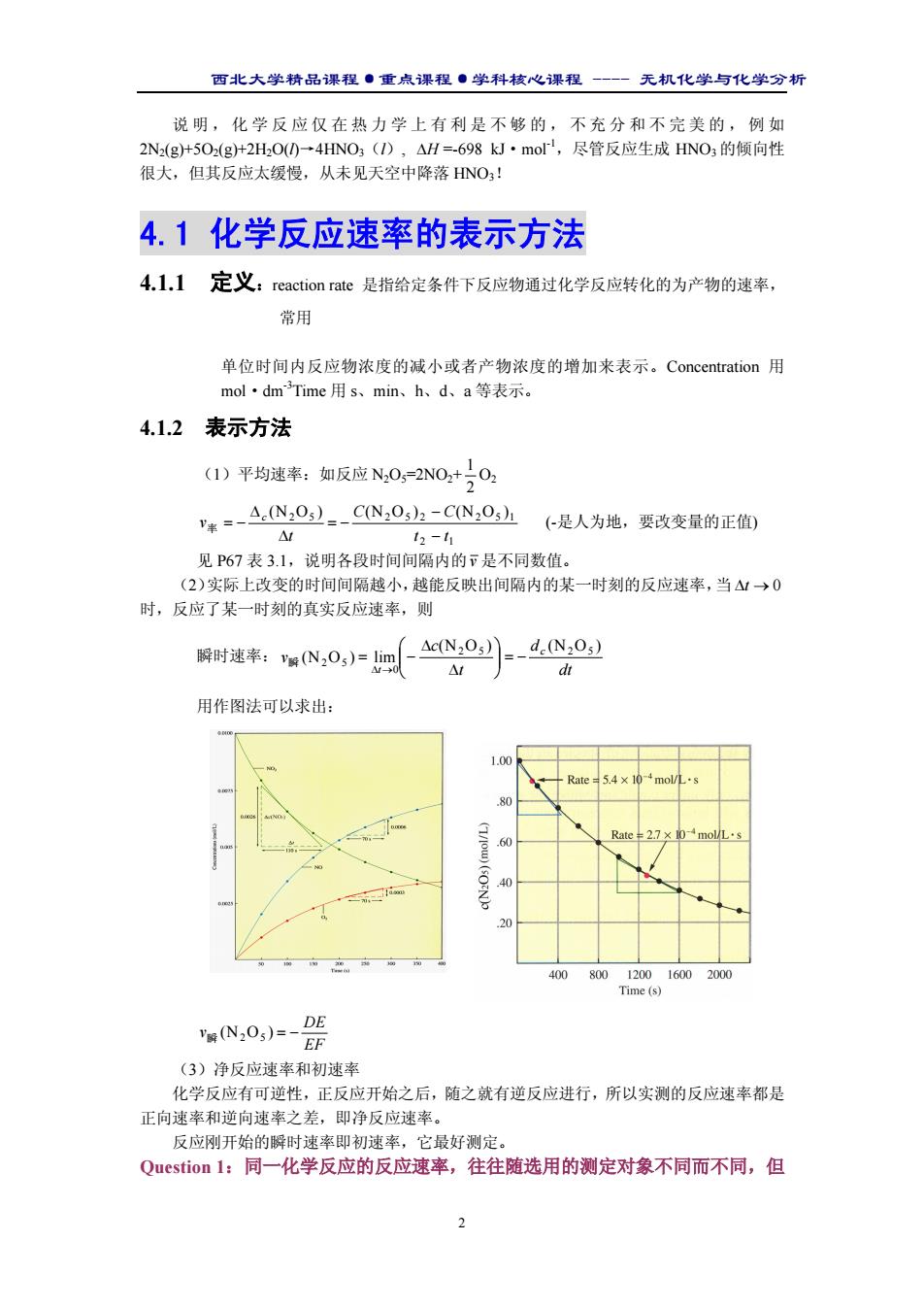
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 2 说明,化学反应仅在热力学上有利是不够的,不充分和不完美的,例如 2N2(g)+5O2(g)+2H2O(l)→4HNO3(l), ∆H =-698 kJ·mol-1,尽管反应生成 HNO3 的倾向性 很大,但其反应太缓慢,从未见天空中降落 HNO3! 4.1 化学反应速率的表示方法 4.1.1 定义:reaction rate 是指给定条件下反应物通过化学反应转化的为产物的速率, 常用 单位时间内反应物浓度的减小或者产物浓度的增加来表示。Concentration 用 mol·dm-3Time 用 s、min、h、d、a 等表示。 4.1.2 表示方法 (1)平均速率:如反应 N2O5=2NO2+ 2 1 O2 2 1 2 5 2 5 2 2 5 1 (N O ) (N O ) (N O ) t t C C t v c − − = − ∆ ∆ 率 = − (-是人为地,要改变量的正值) 见 P67 表 3.1,说明各段时间间隔内的v 是不同数值。 (2)实际上改变的时间间隔越小,越能反映出间隔内的某一时刻的反应速率,当 ∆t → 0 时,反应了某一时刻的真实反应速率,则 瞬时速率: dt d t c v c t (N O ) (N O ) (N O ) lim 2 5 2 5 0 2 5 = − ∆ ∆ = − ∆ → 瞬 用作图法可以求出: EF DE v瞬 (N2O5 ) = − (3)净反应速率和初速率 化学反应有可逆性,正反应开始之后,随之就有逆反应进行,所以实测的反应速率都是 正向速率和逆向速率之差,即净反应速率。 反应刚开始的瞬时速率即初速率,它最好测定。 Question 1:同一化学反应的反应速率,往往随选用的测定对象不同而不同,但
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 2 说明,化学反应仅在热力学上有利是不够的,不充分和不完美的,例如 2N2(g)+5O2(g)+2H2O(l)→4HNO3(l), ∆H =-698 kJ·mol-1,尽管反应生成 HNO3 的倾向性 很大,但其反应太缓慢,从未见天空中降落 HNO3! 4.1 化学反应速率的表示方法 4.1.1 定义:reaction rate 是指给定条件下反应物通过化学反应转化的为产物的速率, 常用 单位时间内反应物浓度的减小或者产物浓度的增加来表示。Concentration 用 mol·dm-3Time 用 s、min、h、d、a 等表示。 4.1.2 表示方法 (1)平均速率:如反应 N2O5=2NO2+ 2 1 O2 2 1 2 5 2 5 2 2 5 1 (N O ) (N O ) (N O ) t t C C t v c − − = − ∆ ∆ 率 = − (-是人为地,要改变量的正值) 见 P67 表 3.1,说明各段时间间隔内的v 是不同数值。 (2)实际上改变的时间间隔越小,越能反映出间隔内的某一时刻的反应速率,当 ∆t → 0 时,反应了某一时刻的真实反应速率,则 瞬时速率: dt d t c v c t (N O ) (N O ) (N O ) lim 2 5 2 5 0 2 5 = − ∆ ∆ = − ∆ → 瞬 用作图法可以求出: EF DE v瞬 (N2O5 ) = − (3)净反应速率和初速率 化学反应有可逆性,正反应开始之后,随之就有逆反应进行,所以实测的反应速率都是 正向速率和逆向速率之差,即净反应速率。 反应刚开始的瞬时速率即初速率,它最好测定。 Question 1:同一化学反应的反应速率,往往随选用的测定对象不同而不同,但

西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 3 为什么针对不同测定对象的速率方程却相同? 如 P66 表 3.1 中,可看出: 表示的实质相同,只是数值不同,必然有内在关系。 对一般反应:a A + b B= g G + h H 的反应速率可表示为: t CA d d − 或 t CB d d − 或 t CG d d 或 t CH d d 如果 a、b、g、h 不等,则它们的关系为: t C t h C t g C t b C a A B G H d 1 d d 1 d d 1 d d 1 d − = − = = 但是,该反应用以上四种物质中任何一种所表示的速率方程都相同,即 n B m v = kCA ⋅C 对不同的测定其 k 不同(速率常数)(kA、KB、KG、KH) 4.2 反应速率理论简介 4.2.1 碰撞理论 Collision theory 1918 年 Lewis 运用气体分子运动论的成果提出的。 (1)碰撞是先决条件,碰撞频率越高,rate 越大。 (2)只有少数碰撞才能导致化学反应。 活化分子组(activation molecule) ① ②要有足够大的能量,以克服无限接近时电子云之间的斥力,从而导致分子中的原 子重排: ③定向碰撞
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 3 为什么针对不同测定对象的速率方程却相同? 如 P66 表 3.1 中,可看出: 表示的实质相同,只是数值不同,必然有内在关系。 对一般反应:a A + b B= g G + h H 的反应速率可表示为: t CA d d − 或 t CB d d − 或 t CG d d 或 t CH d d 如果 a、b、g、h 不等,则它们的关系为: t C t h C t g C t b C a A B G H d 1 d d 1 d d 1 d d 1 d − = − = = 但是,该反应用以上四种物质中任何一种所表示的速率方程都相同,即 n B m v = kCA ⋅C 对不同的测定其 k 不同(速率常数)(kA、KB、KG、KH) 4.2 反应速率理论简介 4.2.1 碰撞理论 Collision theory 1918 年 Lewis 运用气体分子运动论的成果提出的。 (1)碰撞是先决条件,碰撞频率越高,rate 越大。 (2)只有少数碰撞才能导致化学反应。 活化分子组(activation molecule) ① ②要有足够大的能量,以克服无限接近时电子云之间的斥力,从而导致分子中的原 子重排: ③定向碰撞
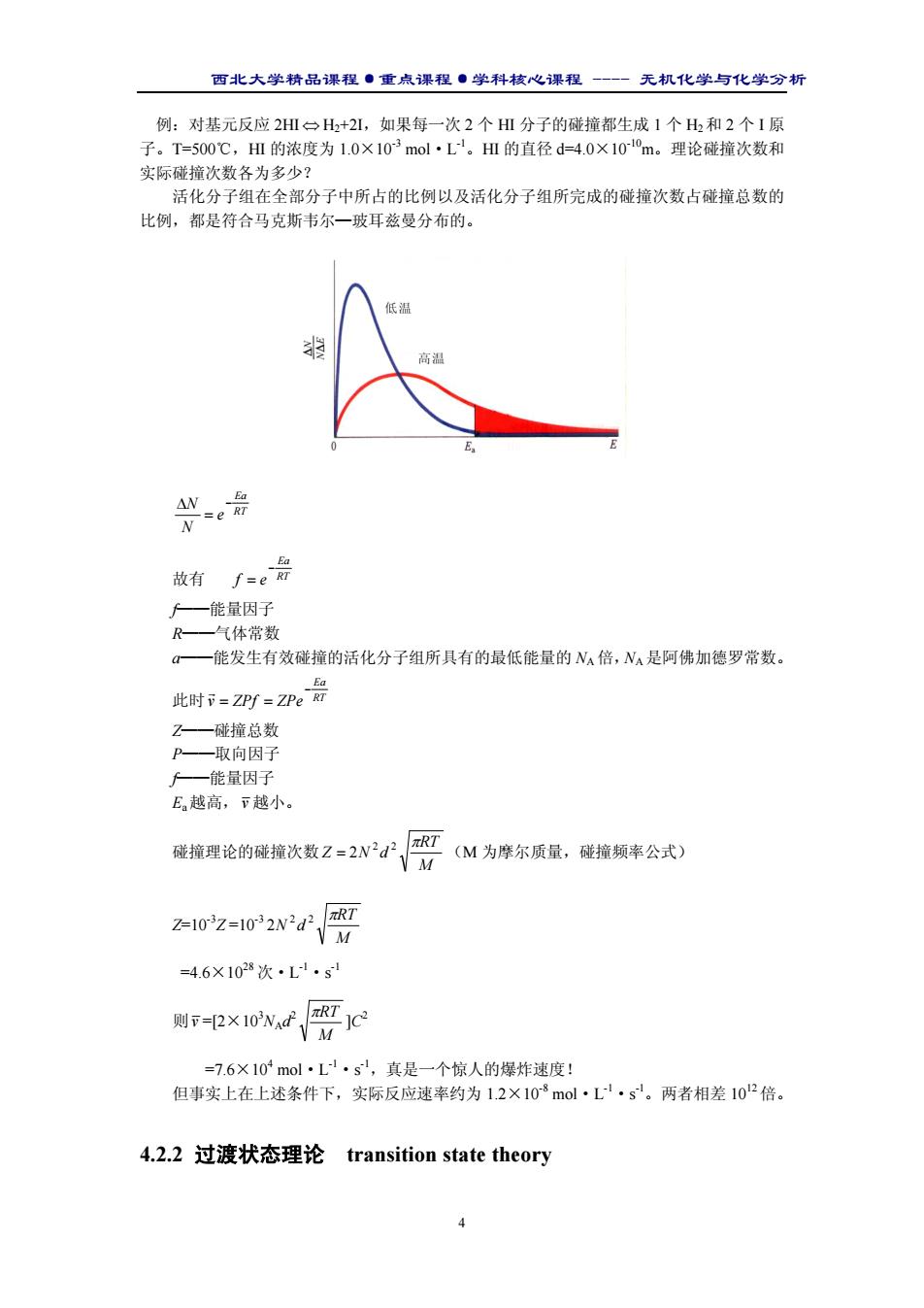
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 4 例:对基元反应 2HI ⇔ H2+2I,如果每一次 2 个 HI 分子的碰撞都生成 1 个 H2和 2 个 I 原 子。T=500℃,HI 的浓度为 1.0×10-3 mol·L-1。HI 的直径 d=4.0×10-10 m。理论碰撞次数和 实际碰撞次数各为多少? 活化分子组在全部分子中所占的比例以及活化分子组所完成的碰撞次数占碰撞总数的 比例,都是符合马克斯韦尔—玻耳兹曼分布的。 RT Ea e N N − = ∆ 故有 RT Ea f e − = f——能量因子 R——气体常数 a——能发生有效碰撞的活化分子组所具有的最低能量的 NA倍,NA是阿佛加德罗常数。 此时 RT Ea v ZPf ZPe − = = r Z——碰撞总数 P——取向因子 f——能量因子 Ea越高,v 越小。 碰撞理论的碰撞次数 M RT Z N d 2 2 π = 2 (M 为摩尔质量,碰撞频率公式) Z=10-3Z =10-3 M RT N d 2 2 π 2 =4.6×1028 次·L-1·s -1 则v =[2×103 NAd2 M πRT ]C2 =7.6×104 mol·L-1·s -1,真是一个惊人的爆炸速度! 但事实上在上述条件下,实际反应速率约为 1.2×10-8 mol·L-1·s -1。两者相差 1012 倍。 4.2.2 过渡状态理论 transition state theory
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 4 例:对基元反应 2HI ⇔ H2+2I,如果每一次 2 个 HI 分子的碰撞都生成 1 个 H2和 2 个 I 原 子。T=500℃,HI 的浓度为 1.0×10-3 mol·L-1。HI 的直径 d=4.0×10-10 m。理论碰撞次数和 实际碰撞次数各为多少? 活化分子组在全部分子中所占的比例以及活化分子组所完成的碰撞次数占碰撞总数的 比例,都是符合马克斯韦尔—玻耳兹曼分布的。 RT Ea e N N − = ∆ 故有 RT Ea f e − = f——能量因子 R——气体常数 a——能发生有效碰撞的活化分子组所具有的最低能量的 NA倍,NA是阿佛加德罗常数。 此时 RT Ea v ZPf ZPe − = = r Z——碰撞总数 P——取向因子 f——能量因子 Ea越高,v 越小。 碰撞理论的碰撞次数 M RT Z N d 2 2 π = 2 (M 为摩尔质量,碰撞频率公式) Z=10-3Z =10-3 M RT N d 2 2 π 2 =4.6×1028 次·L-1·s -1 则v =[2×103 NAd2 M πRT ]C2 =7.6×104 mol·L-1·s -1,真是一个惊人的爆炸速度! 但事实上在上述条件下,实际反应速率约为 1.2×10-8 mol·L-1·s -1。两者相差 1012 倍。 4.2.2 过渡状态理论 transition state theory

西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 5 (1)P94 黑体字,活化络合物(activated complex) A + B—C→ [A.B.C]* →A—B + C 图空 被削弱但未完全断裂 新的化学键开始形成但尚未完全形成。 (2)是一种不稳定状态(P94) (3)这种理论还在发展,但在处理复杂分子间的反应却更有前途。 4.2.3.活化能 activation energy,用 Ea表示 (1)有不同的概念 a. 把反应物分子转变为活化分子所需要的能量。 b. 活化分子所具有的最低能量与反应物分子的平均能量之差。 c. 活化分子的平均能量与反应物分子的平均能量之差。 c 更合理,参考: [1] 韩德刚,印永嘉,化学教育,增刊 1:62(1981) [2] 李大珍,化学教育,1980,5:14 [3] 罗谕然,化学通报,1981,4:50 (2)反应历程(P100 图 4.6) Energy path of the reaction. (3)T 定,活化能一定 不同的反应,活化能不同;不同类型的反应、活化能 Ea相差很大。 2SO2 + O2→2SO3 Ea=251 kJ·mol-1 N2 + 3H2 →Fe 2NH3 Ea=175.5 kJ·mol-1 HCl + NaOH→NaCl + H2O Ea≈20 kJ·mol-1 离子反应和沉淀反应的 Ea都较小。 (4)Ea与反应热效应的关系
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 5 (1)P94 黑体字,活化络合物(activated complex) A + B—C→ [A.B.C]* →A—B + C 图空 被削弱但未完全断裂 新的化学键开始形成但尚未完全形成。 (2)是一种不稳定状态(P94) (3)这种理论还在发展,但在处理复杂分子间的反应却更有前途。 4.2.3.活化能 activation energy,用 Ea表示 (1)有不同的概念 a. 把反应物分子转变为活化分子所需要的能量。 b. 活化分子所具有的最低能量与反应物分子的平均能量之差。 c. 活化分子的平均能量与反应物分子的平均能量之差。 c 更合理,参考: [1] 韩德刚,印永嘉,化学教育,增刊 1:62(1981) [2] 李大珍,化学教育,1980,5:14 [3] 罗谕然,化学通报,1981,4:50 (2)反应历程(P100 图 4.6) Energy path of the reaction. (3)T 定,活化能一定 不同的反应,活化能不同;不同类型的反应、活化能 Ea相差很大。 2SO2 + O2→2SO3 Ea=251 kJ·mol-1 N2 + 3H2 →Fe 2NH3 Ea=175.5 kJ·mol-1 HCl + NaOH→NaCl + H2O Ea≈20 kJ·mol-1 离子反应和沉淀反应的 Ea都较小。 (4)Ea与反应热效应的关系
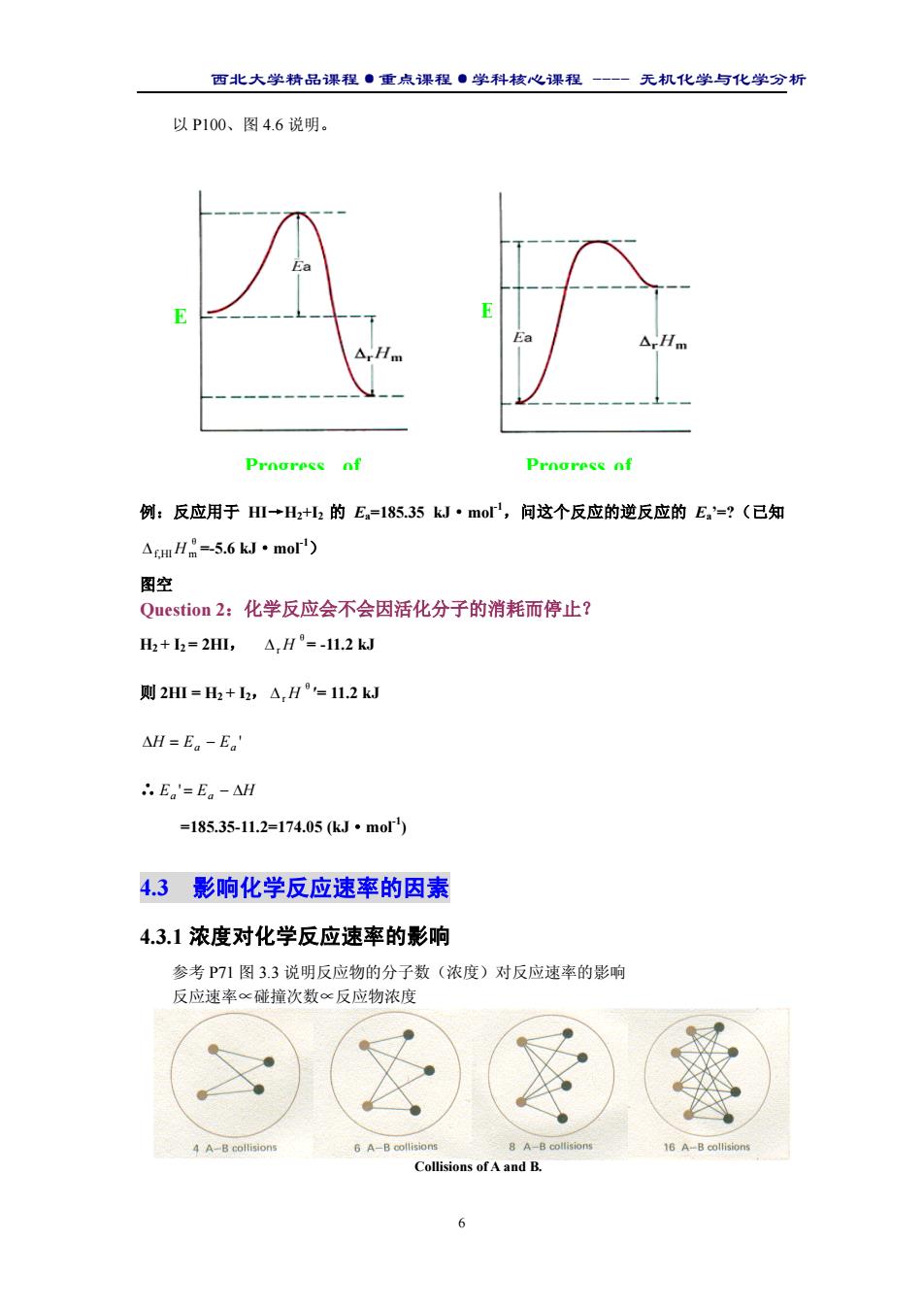
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 6 以 P100、图 4.6 说明。 例:反应用于 HI→H2+I2 的 Ea=185.35 kJ·mol-1,问这个反应的逆反应的 Ea’=?(已知 θ ∆f,HIH m =-5.6 kJ·mol-1) 图空 Question 2:化学反应会不会因活化分子的消耗而停止? H2 + I2 = 2HI, θ ∆r H = -11.2 kJ 则 2HI = H2 + I2, θ ∆r H ′= 11.2 kJ ' ∆H = Ea − Ea ∴ Ea '= Ea − ∆H =185.35-11.2=174.05 (kJ·mol-1) 4.3 影响化学反应速率的因素 4.3.1 浓度对化学反应速率的影响 参考 P71 图 3.3 说明反应物的分子数(浓度)对反应速率的影响 反应速率∝碰撞次数∝反应物浓度 Collisions of A and B. Progress of E Progress of E
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 6 以 P100、图 4.6 说明。 例:反应用于 HI→H2+I2 的 Ea=185.35 kJ·mol-1,问这个反应的逆反应的 Ea’=?(已知 θ ∆f,HIH m =-5.6 kJ·mol-1) 图空 Question 2:化学反应会不会因活化分子的消耗而停止? H2 + I2 = 2HI, θ ∆r H = -11.2 kJ 则 2HI = H2 + I2, θ ∆r H ′= 11.2 kJ ' ∆H = Ea − Ea ∴ Ea '= Ea − ∆H =185.35-11.2=174.05 (kJ·mol-1) 4.3 影响化学反应速率的因素 4.3.1 浓度对化学反应速率的影响 参考 P71 图 3.3 说明反应物的分子数(浓度)对反应速率的影响 反应速率∝碰撞次数∝反应物浓度 Collisions of A and B. Progress of E Progress of E

西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 7 (1) 基元反应的速率方程 rate equation(反应物浓度与反应速率之间的定量关系 (2) 建立在有效碰撞的基础上。 基元反应 elementary reaction(简单反应或元反应):反应物分子在有效碰撞中一步直接 转化为产物的反应。 见 P96~98 及图 4.4 导出速率方程,即说明质量作用定律:v=kC2 (A) 由此可说明v = kCa [A]Cb [B]L 速率常数 rate constant: a. 只与 T 有关而与浓度无关。 b. 若浓度均为单位浓度时,则称为比速率,k 大,速率就大。 c. 注意量纲的问题,n=a+b。 dm3(n-1) • mol-(n-1) • s -1 d. 用不同物质的浓度表示 v 时,k 也不同。 (2)复杂反应(complex reaction 或非基元反应 nonelementary reaction) 即由两个或多个基元反应步骤完成的复杂反应: 如: H2 (g) + I2 (g) = 2HI (g) 由 I2 (g) = I (g) + I (g) H2 (g) + I (g) + I (g) = HI (g) + HI (g) 自然就不能用反应式直接导出速率方程,因为复杂反应式只表达反应物之间的化学计量 关系,不能表达反应过程中质点之间的碰撞关系。 怎么办? a. 先找出决速步骤 rate determining step A2 + B→A2B + → → 2A B A B - (rapid reaction) A 2A 慢反应 (slow reaction) 2 2 快反应 瞬间完成 ∴ ( ) A2 v = kC b. 只能由实验来确定(即使由实验测得的反应级数与反应式中反应物计量之和相等, 该反应也不一定就是基元反应) 例如:H2(g) + I2(g) → 2HI(g) 当反应容积缩小一半,即各反应物浓度扩大 2 倍,v 扩大 4 倍, [H ] [I ] 2 C 2 v = kC 实际上是: I2 = I + I(慢) ① H2 + 2I →v 2HI (快) ② ①是定速步骤,因此这一步骤的 [H ][I ] 1 2 2 v = k ,对①, 1 v = v + k+ [I2]=k- [I]2 [I]2 = − + k k [I2] 代入上式得 − + = k k k v 1 [H2][I2] 令 − + k k k1 =k,得 [H ][I ] 1 2 2 v = k
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 7 (1) 基元反应的速率方程 rate equation(反应物浓度与反应速率之间的定量关系 (2) 建立在有效碰撞的基础上。 基元反应 elementary reaction(简单反应或元反应):反应物分子在有效碰撞中一步直接 转化为产物的反应。 见 P96~98 及图 4.4 导出速率方程,即说明质量作用定律:v=kC2 (A) 由此可说明v = kCa [A]Cb [B]L 速率常数 rate constant: a. 只与 T 有关而与浓度无关。 b. 若浓度均为单位浓度时,则称为比速率,k 大,速率就大。 c. 注意量纲的问题,n=a+b。 dm3(n-1) • mol-(n-1) • s -1 d. 用不同物质的浓度表示 v 时,k 也不同。 (2)复杂反应(complex reaction 或非基元反应 nonelementary reaction) 即由两个或多个基元反应步骤完成的复杂反应: 如: H2 (g) + I2 (g) = 2HI (g) 由 I2 (g) = I (g) + I (g) H2 (g) + I (g) + I (g) = HI (g) + HI (g) 自然就不能用反应式直接导出速率方程,因为复杂反应式只表达反应物之间的化学计量 关系,不能表达反应过程中质点之间的碰撞关系。 怎么办? a. 先找出决速步骤 rate determining step A2 + B→A2B + → → 2A B A B - (rapid reaction) A 2A 慢反应 (slow reaction) 2 2 快反应 瞬间完成 ∴ ( ) A2 v = kC b. 只能由实验来确定(即使由实验测得的反应级数与反应式中反应物计量之和相等, 该反应也不一定就是基元反应) 例如:H2(g) + I2(g) → 2HI(g) 当反应容积缩小一半,即各反应物浓度扩大 2 倍,v 扩大 4 倍, [H ] [I ] 2 C 2 v = kC 实际上是: I2 = I + I(慢) ① H2 + 2I →v 2HI (快) ② ①是定速步骤,因此这一步骤的 [H ][I ] 1 2 2 v = k ,对①, 1 v = v + k+ [I2]=k- [I]2 [I]2 = − + k k [I2] 代入上式得 − + = k k k v 1 [H2][I2] 令 − + k k k1 =k,得 [H ][I ] 1 2 2 v = k

西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 8 与从方程式书写一致,但它绝不是基元反应! 光化学实验证明: 1967 年有人在低温下、光照进行反应,发现可以加速反应,λ=578nm,只能使 I2分子 裂解,并不能裂解 H2 分子,结构理论认为 H2 和 I2 直接反应是禁阻的。 (3)反应分子数和反应级数 reaction order 反应级数:速率方程中各反应物浓度的指数和。 注意: a. 反应 H2 + Br2→2HBr Br [HBr] 1 [H ][Br ] d d[ ] 0.5 2 2 k' k t HBr + = 就属于不能纳入通式的形式,反应级数无意义。 b. 反应级数是几,就是几级反应。 c. 允许值是由于反应的复杂性,有的反应是由某种因素所控制,有的反应是由许多基 元反应组成,因此出现一、零、分数、负数或其它更复杂的情况就不足为奇了。(可 有许多不同的测定如 TG、DTG、DSG、DTA 等) d. k 的单位与 n 有关。 一级反应:k 的单位为 s -1 或 min-1 等; 二级反应:dm3 ·mol-1、s -1 或 dm3 ·mol-1、min-1 等。 三级反应:dm6 ·mol-2、s -1 或 dm6 ·mol-2、min-1 等。 (4)书写速率方程式要注意的(P71~72) 例题:测定反应 2H2+2NO→2H2O+N2 速率的实验如下: No C(NO)初 C(H2)初/mol·dm-3 形成 N2(g)的起始速率 v/mol·dm-3 1 6.00×10 –3 1.00×10 –3 3.19×10 –3 2 6.00×10 –3 2.00×10 –3 6.36×10 –3 3 6.00×10 –3 3.00×10 –3 9.56×10 –3 4 1.00×10 –3 6.00×10 –3 0.48×10 –3 5 2.00×10 –3 6.00×10 –3 1.92×10 –3 6 3.00×10 -3 6.00×10 -3 4.30×10 -3 T=1073K 比较 1,2,3,C(NO)一定,v∝[H2] 比较 4,5,6,C(NO)一定,v∝[NO]2 一并考虑的 v∝[H2][NO]2 ∴v=k[H2][NO]2 而不是 v=k[H2] 2 [NO]2 ,反应级数为 3 而不是 4。 将 No.1 的数据代入(用那个算都一样,说明 T 定 v 不因 C 变而变) 3 3 1 3 3 1 2 3 3 1 (1.00 10 mol dm s )(6.00 10 mol dm s ) 3.19 10 mol dm s − − − − − − − − − × ⋅ ⋅ × ⋅ ⋅ × ⋅ ⋅ k = =8.86×104 dm6 ·mol-2·s -1
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 8 与从方程式书写一致,但它绝不是基元反应! 光化学实验证明: 1967 年有人在低温下、光照进行反应,发现可以加速反应,λ=578nm,只能使 I2分子 裂解,并不能裂解 H2 分子,结构理论认为 H2 和 I2 直接反应是禁阻的。 (3)反应分子数和反应级数 reaction order 反应级数:速率方程中各反应物浓度的指数和。 注意: a. 反应 H2 + Br2→2HBr Br [HBr] 1 [H ][Br ] d d[ ] 0.5 2 2 k' k t HBr + = 就属于不能纳入通式的形式,反应级数无意义。 b. 反应级数是几,就是几级反应。 c. 允许值是由于反应的复杂性,有的反应是由某种因素所控制,有的反应是由许多基 元反应组成,因此出现一、零、分数、负数或其它更复杂的情况就不足为奇了。(可 有许多不同的测定如 TG、DTG、DSG、DTA 等) d. k 的单位与 n 有关。 一级反应:k 的单位为 s -1 或 min-1 等; 二级反应:dm3 ·mol-1、s -1 或 dm3 ·mol-1、min-1 等。 三级反应:dm6 ·mol-2、s -1 或 dm6 ·mol-2、min-1 等。 (4)书写速率方程式要注意的(P71~72) 例题:测定反应 2H2+2NO→2H2O+N2 速率的实验如下: No C(NO)初 C(H2)初/mol·dm-3 形成 N2(g)的起始速率 v/mol·dm-3 1 6.00×10 –3 1.00×10 –3 3.19×10 –3 2 6.00×10 –3 2.00×10 –3 6.36×10 –3 3 6.00×10 –3 3.00×10 –3 9.56×10 –3 4 1.00×10 –3 6.00×10 –3 0.48×10 –3 5 2.00×10 –3 6.00×10 –3 1.92×10 –3 6 3.00×10 -3 6.00×10 -3 4.30×10 -3 T=1073K 比较 1,2,3,C(NO)一定,v∝[H2] 比较 4,5,6,C(NO)一定,v∝[NO]2 一并考虑的 v∝[H2][NO]2 ∴v=k[H2][NO]2 而不是 v=k[H2] 2 [NO]2 ,反应级数为 3 而不是 4。 将 No.1 的数据代入(用那个算都一样,说明 T 定 v 不因 C 变而变) 3 3 1 3 3 1 2 3 3 1 (1.00 10 mol dm s )(6.00 10 mol dm s ) 3.19 10 mol dm s − − − − − − − − − × ⋅ ⋅ × ⋅ ⋅ × ⋅ ⋅ k = =8.86×104 dm6 ·mol-2·s -1

西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 9 此题要求: (1)决定反应级数; (2)写出速率方程; (3)求 k。 4.3.2 温度对化学反应速率的影响 温度对不同反应的影响是不同的: 原因:(1) a 分子运动速率加快,反应物分子碰撞频率增大。 b 活化分子组的百分数增大,有效碰撞的百分数增加。 粗略的估计(Vant Hoff 规则) 2 ~ 4 10 = + t t k k (2)无论吸热还是放热反应,温度升高反应速率都是加快,反应中反应物必须爬过一 个能垒才能进行,升高温度有利于反应物能量的提高,可加快反应的进行。 (3)Arrhenius 的反应速率指数定律(v 与 T 的定量关系) RT Ea k Ae− = A——指前因子或频率因子 a. 对指定反应,A 与 C、T 无关的常数; b. 不同的反应,A 不同; c. A 一般是个较大数值,如二级简反应为 1012·mol-1·dm-3·s -1 d. A 与 k 有相同的单位。 指数形式 对数形式 ln( /[ ]) 1 ln( /[ ]) A A R T E k k a + = − lg( /[ ]) 1 2.303 lg( /[ ]) A A R T E k k a + = − Ea即活化能,与温度有关(可有不同的情况) 求 Ea: a. 实验作图法(P72 之步骤) b. 代入法(由不同 T 值的 k 计算) c. 从键能估算(物化课再讲) 解释 P73 图 3.4 4.3.3 反应物之间的接触状况对反应速率的影响 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ 铁 铁
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 9 此题要求: (1)决定反应级数; (2)写出速率方程; (3)求 k。 4.3.2 温度对化学反应速率的影响 温度对不同反应的影响是不同的: 原因:(1) a 分子运动速率加快,反应物分子碰撞频率增大。 b 活化分子组的百分数增大,有效碰撞的百分数增加。 粗略的估计(Vant Hoff 规则) 2 ~ 4 10 = + t t k k (2)无论吸热还是放热反应,温度升高反应速率都是加快,反应中反应物必须爬过一 个能垒才能进行,升高温度有利于反应物能量的提高,可加快反应的进行。 (3)Arrhenius 的反应速率指数定律(v 与 T 的定量关系) RT Ea k Ae− = A——指前因子或频率因子 a. 对指定反应,A 与 C、T 无关的常数; b. 不同的反应,A 不同; c. A 一般是个较大数值,如二级简反应为 1012·mol-1·dm-3·s -1 d. A 与 k 有相同的单位。 指数形式 对数形式 ln( /[ ]) 1 ln( /[ ]) A A R T E k k a + = − lg( /[ ]) 1 2.303 lg( /[ ]) A A R T E k k a + = − Ea即活化能,与温度有关(可有不同的情况) 求 Ea: a. 实验作图法(P72 之步骤) b. 代入法(由不同 T 值的 k 计算) c. 从键能估算(物化课再讲) 解释 P73 图 3.4 4.3.3 反应物之间的接触状况对反应速率的影响 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ 铁 铁

西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 10 P99~100 4.3.4 催化剂对反应速率的影响 (1)Catalyst 的定义(P74) 正催化剂与负催化剂 助催化剂 promoter (2)催化作用机理:降低活化能,改变了反应机理,但对热力学上不能进行的反应是 无能为力的。P73 图 3.6(催化剂不会改变体系的平衡状态,因为它同等程度地降 低正逆反应的活化能,不能改变反应的热效应。) (3)均相催化与多相催化 a. 物理吸附和化学吸附 b. 解释图 3.6(P75) c. 催化剂的中毒和活化 d. 催化剂载体(多孔物质、增大吸附表面积) e. 催化剂的选择性 Energy path of the decomposition of H2O2, catalyzed and uncatalyzed
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 10 P99~100 4.3.4 催化剂对反应速率的影响 (1)Catalyst 的定义(P74) 正催化剂与负催化剂 助催化剂 promoter (2)催化作用机理:降低活化能,改变了反应机理,但对热力学上不能进行的反应是 无能为力的。P73 图 3.6(催化剂不会改变体系的平衡状态,因为它同等程度地降 低正逆反应的活化能,不能改变反应的热效应。) (3)均相催化与多相催化 a. 物理吸附和化学吸附 b. 解释图 3.6(P75) c. 催化剂的中毒和活化 d. 催化剂载体(多孔物质、增大吸附表面积) e. 催化剂的选择性 Energy path of the decomposition of H2O2, catalyzed and uncatalyzed