
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 1 第 1 章 原子结构和元素周期表 Chapter 1 Atomic Structure and Periodic Table of Elements 教学要求 1. 初步了解原子核外电子运动的近代概念、原子能级、波粒二象性、原子轨道(波函 数)和电子云概念。 2. 熟悉四个量子数对核外电子运动状态的描述,掌握四个量子数的物理意义、取值范 围; 3. 熟悉 s、p、d 原子轨道的形状和方向; 4. 理解原子结构的近似能级图,掌握原子核外电子排布的一般规则和 s、p、d、f 区 元素的原子结构特点; 5. 会从原子的电子层结构了解元素性质,熟悉原子半径、电离能、电子亲合能和电负 性的周期性变化。 课时分配(8 学时) 1.原子结构理论的发展和亚原子粒子(3 学时) 微观粒子的波粒二象性: 玻尔模型 波动力学模型 2.原子轨道概念的图形描述及四个量子数(3 学时) 对核外电子运动状态的描述 3.周期表与原子结构(2 学时) 原子参数 1.1 亚原子粒子 化学是一门发展极为迅速而其信息量又十分巨大的学科。就化学研究的对象,可分为下 面的各个层次: 夸克 质子 中子 原子核 电子 原子 (离子) 分子 微观 (宇观) 宇宙 单质 化合物 星体 宏观 纳 米 材料 (介观) 夸克 质子 中子 原子核 电子 原子 (离子) 分子 微观 夸克 质子 中子 原子核 电子 原子 (离子) 分子 微观 夸克 质子 中子 原子核 电子 原子 (离子) 分子 微观 (宇观) 宇宙 单质 化合物 星体 宏观 纳 米 材料 (介观)
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 1 第 1 章 原子结构和元素周期表 Chapter 1 Atomic Structure and Periodic Table of Elements 教学要求 1. 初步了解原子核外电子运动的近代概念、原子能级、波粒二象性、原子轨道(波函 数)和电子云概念。 2. 熟悉四个量子数对核外电子运动状态的描述,掌握四个量子数的物理意义、取值范 围; 3. 熟悉 s、p、d 原子轨道的形状和方向; 4. 理解原子结构的近似能级图,掌握原子核外电子排布的一般规则和 s、p、d、f 区 元素的原子结构特点; 5. 会从原子的电子层结构了解元素性质,熟悉原子半径、电离能、电子亲合能和电负 性的周期性变化。 课时分配(8 学时) 1.原子结构理论的发展和亚原子粒子(3 学时) 微观粒子的波粒二象性: 玻尔模型 波动力学模型 2.原子轨道概念的图形描述及四个量子数(3 学时) 对核外电子运动状态的描述 3.周期表与原子结构(2 学时) 原子参数 1.1 亚原子粒子 化学是一门发展极为迅速而其信息量又十分巨大的学科。就化学研究的对象,可分为下 面的各个层次: 夸克 质子 中子 原子核 电子 原子 (离子) 分子 微观 (宇观) 宇宙 单质 化合物 星体 宏观 纳 米 材料 (介观) 夸克 质子 中子 原子核 电子 原子 (离子) 分子 微观 夸克 质子 中子 原子核 电子 原子 (离子) 分子 微观 夸克 质子 中子 原子核 电子 原子 (离子) 分子 微观 (宇观) 宇宙 单质 化合物 星体 宏观 纳 米 材料 (介观)
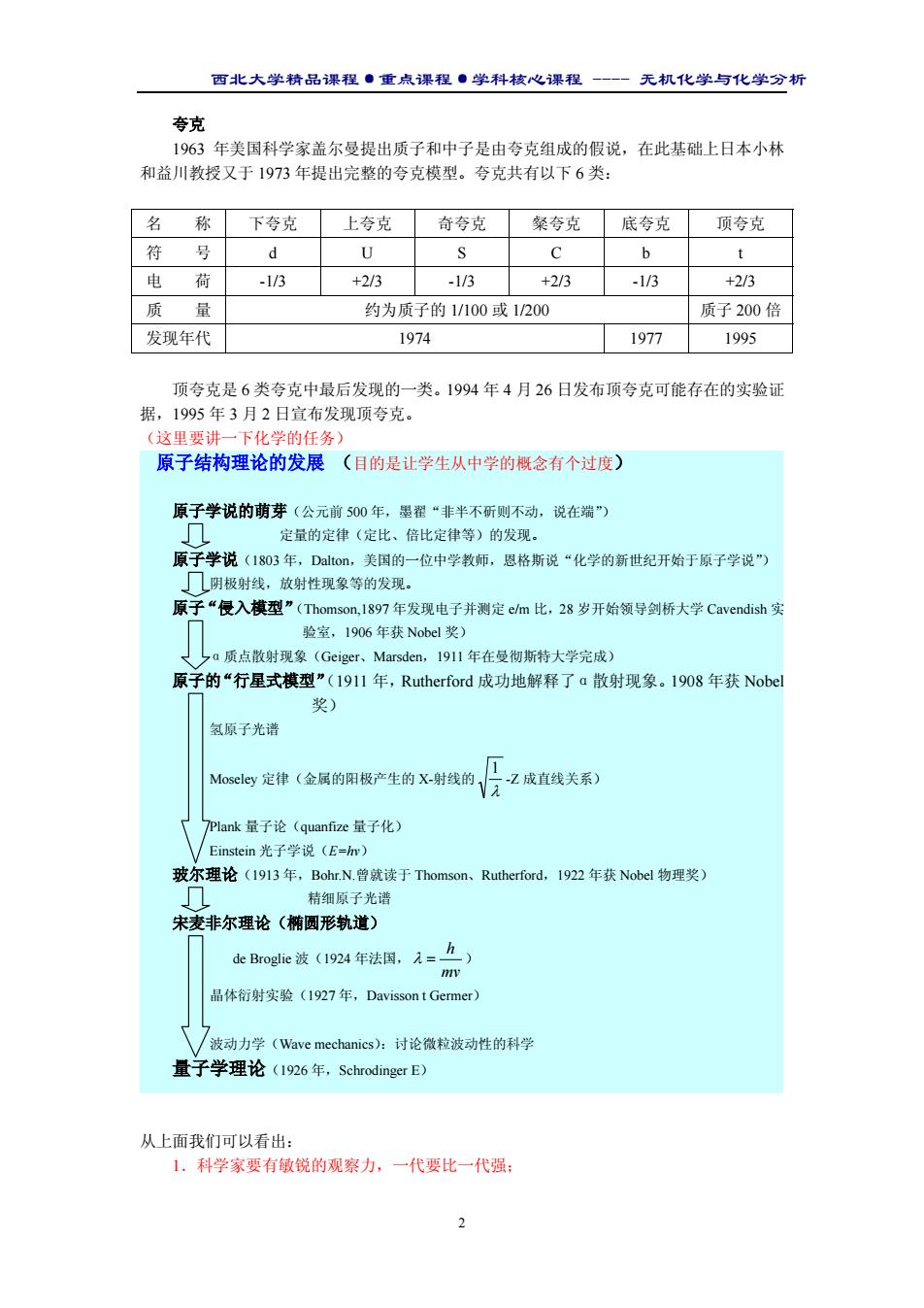
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 2 夸克 1963 年美国科学家盖尔曼提出质子和中子是由夸克组成的假说,在此基础上日本小林 和益川教授又于 1973 年提出完整的夸克模型。夸克共有以下 6 类: 名 称 下夸克 上夸克 奇夸克 粲夸克 底夸克 顶夸克 符 号 d U S C b t 电 荷 -1/3 +2/3 -1/3 +2/3 -1/3 +2/3 质 量 约为质子的 1/100 或 1/200 质子 200 倍 发现年代 1974 1977 1995 顶夸克是 6 类夸克中最后发现的一类。1994 年 4 月 26 日发布顶夸克可能存在的实验证 据,1995 年 3 月 2 日宣布发现顶夸克。 (这里要讲一下化学的任务) 原子结构理论的发展 (目的是让学生从中学的概念有个过度) 原子学说的萌芽(公元前 500 年,墨翟“非半不斫则不动,说在端”) 定量的定律(定比、倍比定律等)的发现。 原子学说(1803 年,Dalton,美国的一位中学教师,恩格斯说“化学的新世纪开始于原子学说”) 阴极射线,放射性现象等的发现。 原子“侵入模型”(Thomson,1897 年发现电子并测定 e/m 比,28 岁开始领导剑桥大学 Cavendish 实 验室,1906 年获 Nobel 奖) α质点散射现象(Geiger、Marsden,1911 年在曼彻斯特大学完成) 原子的“行星式模型”(1911 年,Rutherford 成功地解释了α散射现象。1908 年获 Nobel 奖) 氢原子光谱 Moseley 定律(金属的阳极产生的 X-射线的 λ 1 -Z 成直线关系) Plank 量子论(quanfize 量子化) Einstein 光子学说(E=hv) 玻尔理论(1913 年,Bohr.N.曾就读于 Thomson、Rutherford,1922 年获 Nobel 物理奖) 精细原子光谱 宋麦非尔理论(椭圆形轨道) de Broglie 波(1924 年法国, mv h λ = ) 晶体衍射实验(1927 年,Davisson t Germer) 波动力学(Wave mechanics):讨论微粒波动性的科学 量子学理论(1926 年,Schrodinger E) 从上面我们可以看出: 1.科学家要有敏锐的观察力,一代要比一代强;
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 2 夸克 1963 年美国科学家盖尔曼提出质子和中子是由夸克组成的假说,在此基础上日本小林 和益川教授又于 1973 年提出完整的夸克模型。夸克共有以下 6 类: 名 称 下夸克 上夸克 奇夸克 粲夸克 底夸克 顶夸克 符 号 d U S C b t 电 荷 -1/3 +2/3 -1/3 +2/3 -1/3 +2/3 质 量 约为质子的 1/100 或 1/200 质子 200 倍 发现年代 1974 1977 1995 顶夸克是 6 类夸克中最后发现的一类。1994 年 4 月 26 日发布顶夸克可能存在的实验证 据,1995 年 3 月 2 日宣布发现顶夸克。 (这里要讲一下化学的任务) 原子结构理论的发展 (目的是让学生从中学的概念有个过度) 原子学说的萌芽(公元前 500 年,墨翟“非半不斫则不动,说在端”) 定量的定律(定比、倍比定律等)的发现。 原子学说(1803 年,Dalton,美国的一位中学教师,恩格斯说“化学的新世纪开始于原子学说”) 阴极射线,放射性现象等的发现。 原子“侵入模型”(Thomson,1897 年发现电子并测定 e/m 比,28 岁开始领导剑桥大学 Cavendish 实 验室,1906 年获 Nobel 奖) α质点散射现象(Geiger、Marsden,1911 年在曼彻斯特大学完成) 原子的“行星式模型”(1911 年,Rutherford 成功地解释了α散射现象。1908 年获 Nobel 奖) 氢原子光谱 Moseley 定律(金属的阳极产生的 X-射线的 λ 1 -Z 成直线关系) Plank 量子论(quanfize 量子化) Einstein 光子学说(E=hv) 玻尔理论(1913 年,Bohr.N.曾就读于 Thomson、Rutherford,1922 年获 Nobel 物理奖) 精细原子光谱 宋麦非尔理论(椭圆形轨道) de Broglie 波(1924 年法国, mv h λ = ) 晶体衍射实验(1927 年,Davisson t Germer) 波动力学(Wave mechanics):讨论微粒波动性的科学 量子学理论(1926 年,Schrodinger E) 从上面我们可以看出: 1.科学家要有敏锐的观察力,一代要比一代强;
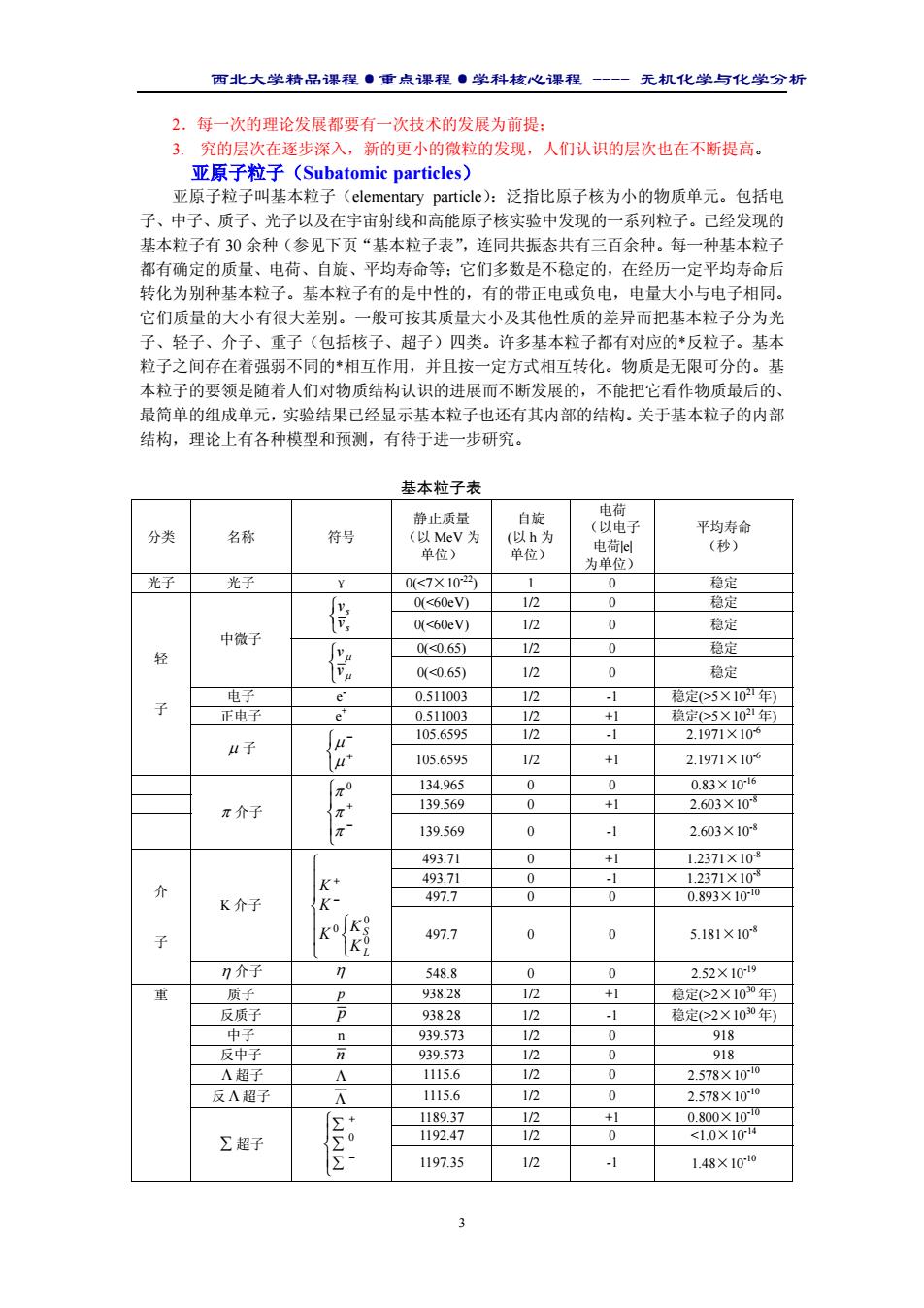
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 3 2.每一次的理论发展都要有一次技术的发展为前提; 3. 究的层次在逐步深入,新的更小的微粒的发现,人们认识的层次也在不断提高。 亚原子粒子(Subatomic particles) 亚原子粒子叫基本粒子(elementary particle):泛指比原子核为小的物质单元。包括电 子、中子、质子、光子以及在宇宙射线和高能原子核实验中发现的一系列粒子。已经发现的 基本粒子有 30 余种(参见下页“基本粒子表”,连同共振态共有三百余种。每一种基本粒子 都有确定的质量、电荷、自旋、平均寿命等;它们多数是不稳定的,在经历一定平均寿命后 转化为别种基本粒子。基本粒子有的是中性的,有的带正电或负电,电量大小与电子相同。 它们质量的大小有很大差别。一般可按其质量大小及其他性质的差异而把基本粒子分为光 子、轻子、介子、重子(包括核子、超子)四类。许多基本粒子都有对应的*反粒子。基本 粒子之间存在着强弱不同的*相互作用,并且按一定方式相互转化。物质是无限可分的。基 本粒子的要领是随着人们对物质结构认识的进展而不断发展的,不能把它看作物质最后的、 最简单的组成单元,实验结果已经显示基本粒子也还有其内部的结构。关于基本粒子的内部 结构,理论上有各种模型和预测,有待于进一步研究。 基本粒子表 分类 名称 符号 静止质量 (以 MeV 为 单位) 自旋 (以 h 为 单位) 电荷 (以电子 电荷|e| 为单位) 平均寿命 (秒) 光子 光子 γ 0(5×1021年) 正电子 e+ 0.511003 1/2 +1 稳定(>5×1021年) 105.6595 1/2 -1 2.1971×10-6 轻 子 µ 子 + − µ µ 105.6595 1/2 +1 2.1971×10-6 134.965 0 0 0.83×10-16 139.569 0 +1 2.603×10-8 π 介子 − + π π π0 139.569 0 -1 2.603×10-8 493.71 0 +1 1.2371×10-8 493.71 0 -1 1.2371×10-8 497.7 0 0 0.893×10-10 K 介子 − + 0 0 0 L S K K K K K 497.7 0 0 5.181×10-8 介 子 η 介子 η 548.8 0 0 2.52×10-19 质子 p 938.28 1/2 +1 稳定(>2×1030年) 反质子 p 938.28 1/2 -1 稳定(>2×1030年) 中子 n 939.573 1/2 0 918 反中子 n 939.573 1/2 0 918 Λ 超子 Λ 1115.6 1/2 0 2.578×10-10 反 Λ 超子 Λ 1115.6 1/2 0 2.578×10-10 1189.37 1/2 +1 0.800×10-10 1192.47 1/2 0 <1.0×10-14 重 ∑ 超子 ∑ ∑ ∑ − + 0 1197.35 1/2 -1 1.48×10-10
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 3 2.每一次的理论发展都要有一次技术的发展为前提; 3. 究的层次在逐步深入,新的更小的微粒的发现,人们认识的层次也在不断提高。 亚原子粒子(Subatomic particles) 亚原子粒子叫基本粒子(elementary particle):泛指比原子核为小的物质单元。包括电 子、中子、质子、光子以及在宇宙射线和高能原子核实验中发现的一系列粒子。已经发现的 基本粒子有 30 余种(参见下页“基本粒子表”,连同共振态共有三百余种。每一种基本粒子 都有确定的质量、电荷、自旋、平均寿命等;它们多数是不稳定的,在经历一定平均寿命后 转化为别种基本粒子。基本粒子有的是中性的,有的带正电或负电,电量大小与电子相同。 它们质量的大小有很大差别。一般可按其质量大小及其他性质的差异而把基本粒子分为光 子、轻子、介子、重子(包括核子、超子)四类。许多基本粒子都有对应的*反粒子。基本 粒子之间存在着强弱不同的*相互作用,并且按一定方式相互转化。物质是无限可分的。基 本粒子的要领是随着人们对物质结构认识的进展而不断发展的,不能把它看作物质最后的、 最简单的组成单元,实验结果已经显示基本粒子也还有其内部的结构。关于基本粒子的内部 结构,理论上有各种模型和预测,有待于进一步研究。 基本粒子表 分类 名称 符号 静止质量 (以 MeV 为 单位) 自旋 (以 h 为 单位) 电荷 (以电子 电荷|e| 为单位) 平均寿命 (秒) 光子 光子 γ 0(5×1021年) 正电子 e+ 0.511003 1/2 +1 稳定(>5×1021年) 105.6595 1/2 -1 2.1971×10-6 轻 子 µ 子 + − µ µ 105.6595 1/2 +1 2.1971×10-6 134.965 0 0 0.83×10-16 139.569 0 +1 2.603×10-8 π 介子 − + π π π0 139.569 0 -1 2.603×10-8 493.71 0 +1 1.2371×10-8 493.71 0 -1 1.2371×10-8 497.7 0 0 0.893×10-10 K 介子 − + 0 0 0 L S K K K K K 497.7 0 0 5.181×10-8 介 子 η 介子 η 548.8 0 0 2.52×10-19 质子 p 938.28 1/2 +1 稳定(>2×1030年) 反质子 p 938.28 1/2 -1 稳定(>2×1030年) 中子 n 939.573 1/2 0 918 反中子 n 939.573 1/2 0 918 Λ 超子 Λ 1115.6 1/2 0 2.578×10-10 反 Λ 超子 Λ 1115.6 1/2 0 2.578×10-10 1189.37 1/2 +1 0.800×10-10 1192.47 1/2 0 <1.0×10-14 重 ∑ 超子 ∑ ∑ ∑ − + 0 1197.35 1/2 -1 1.48×10-10
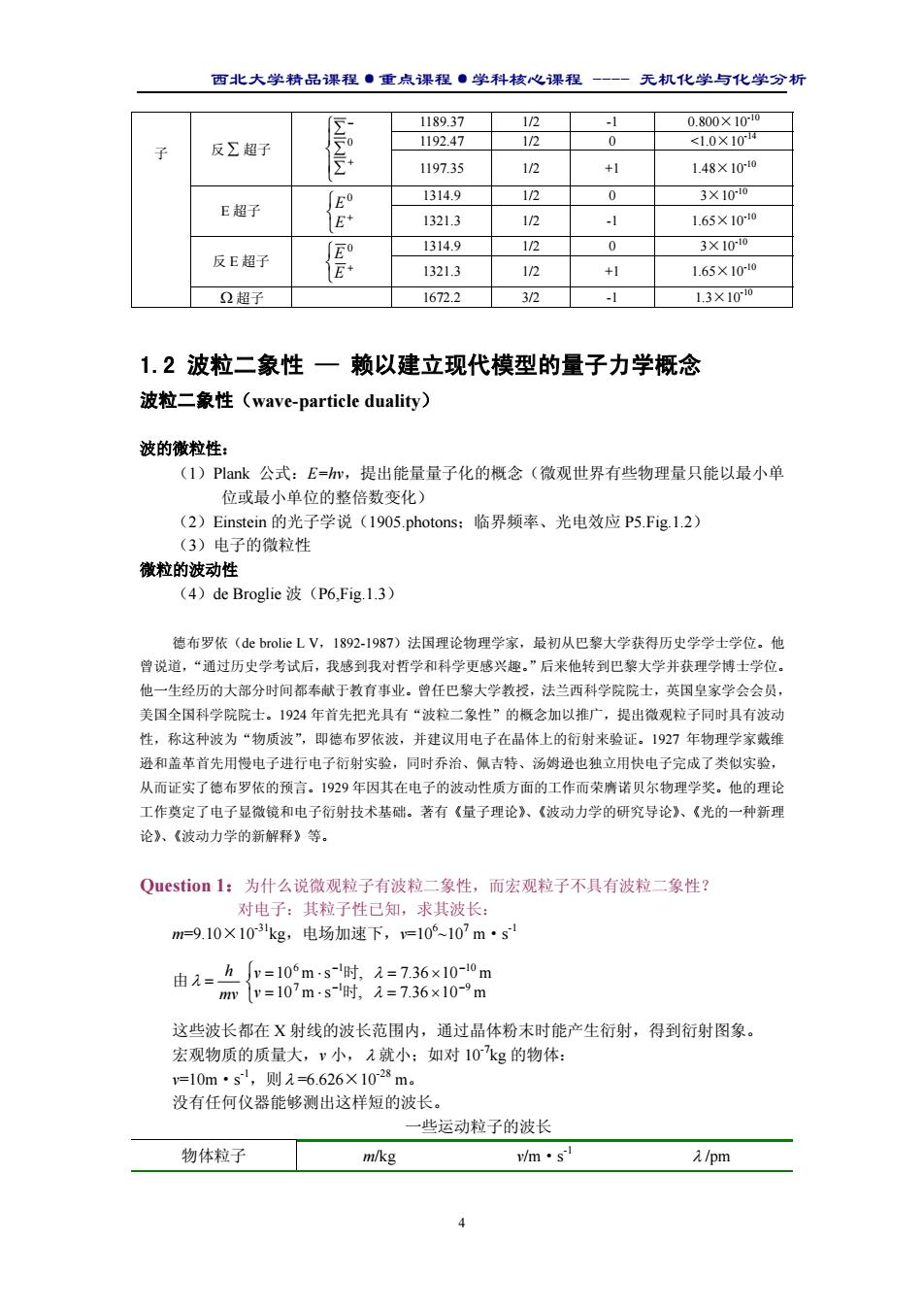
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 4 1189.37 1/2 -1 0.800×10-10 1192.47 1/2 0 <1.0×10-14 反 ∑ 超子 ∑ ∑ ∑ + − 0 1197.35 1/2 +1 1.48×10-10 1314.9 1/2 0 3×10-10 E 超子 + E E0 1321.3 1/2 -1 1.65×10-10 1314.9 1/2 0 3×10-10 反 E 超子 + E E 0 1321.3 1/2 +1 1.65×10-10 子 Ω 超子 1672.2 3/2 -1 1.3×10-10 1.2 波粒二象性 — 赖以建立现代模型的量子力学概念 波粒二象性(wave-particle duality) 波的微粒性: (1)Plank 公式:E=hv,提出能量量子化的概念(微观世界有些物理量只能以最小单 位或最小单位的整倍数变化) (2)Einstein 的光子学说(1905.photons;临界频率、光电效应 P5.Fig.1.2) (3)电子的微粒性 微粒的波动性 (4)de Broglie 波(P6,Fig.1.3) 德布罗依(de brolie L V,1892-1987)法国理论物理学家,最初从巴黎大学获得历史学学士学位。他 曾说道,“通过历史学考试后,我感到我对哲学和科学更感兴趣。”后来他转到巴黎大学并获理学博士学位。 他一生经历的大部分时间都奉献于教育事业。曾任巴黎大学教授,法兰西科学院院士,英国皇家学会会员, 美国全国科学院院士。1924 年首先把光具有“波粒二象性”的概念加以推广,提出微观粒子同时具有波动 性,称这种波为“物质波”,即德布罗依波,并建议用电子在晶体上的衍射来验证。1927 年物理学家戴维 逊和盖革首先用慢电子进行电子衍射实验,同时乔治、佩吉特、汤姆逊也独立用快电子完成了类似实验, 从而证实了德布罗依的预言。1929 年因其在电子的波动性质方面的工作而荣膺诺贝尔物理学奖。他的理论 工作奠定了电子显微镜和电子衍射技术基础。著有《量子理论》、《波动力学的研究导论》、《光的一种新理 论》、《波动力学的新解释》等。 Question 1:为什么说微观粒子有波粒二象性,而宏观粒子不具有波粒二象性? 对电子:其粒子性已知,求其波长: m=9.10×10-31kg,电场加速下,v=106 ~107 m·s -1 由 mv h λ = = ⋅ = × = ⋅ = × − − − − 10 m s , 7.36 10 m 10 m s , 7.36 10 m 7 1 9 6 1 10 λ λ 时 时 v v 这些波长都在 X 射线的波长范围内,通过晶体粉末时能产生衍射,得到衍射图象。 宏观物质的质量大,v 小,λ 就小;如对 10-7kg 的物体: v=10m·s -1,则λ =6.626×10-28 m。 没有任何仪器能够测出这样短的波长。 一些运动粒子的波长 物体粒子 m/kg v/m·s -1 λ /pm
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 4 1189.37 1/2 -1 0.800×10-10 1192.47 1/2 0 <1.0×10-14 反 ∑ 超子 ∑ ∑ ∑ + − 0 1197.35 1/2 +1 1.48×10-10 1314.9 1/2 0 3×10-10 E 超子 + E E0 1321.3 1/2 -1 1.65×10-10 1314.9 1/2 0 3×10-10 反 E 超子 + E E 0 1321.3 1/2 +1 1.65×10-10 子 Ω 超子 1672.2 3/2 -1 1.3×10-10 1.2 波粒二象性 — 赖以建立现代模型的量子力学概念 波粒二象性(wave-particle duality) 波的微粒性: (1)Plank 公式:E=hv,提出能量量子化的概念(微观世界有些物理量只能以最小单 位或最小单位的整倍数变化) (2)Einstein 的光子学说(1905.photons;临界频率、光电效应 P5.Fig.1.2) (3)电子的微粒性 微粒的波动性 (4)de Broglie 波(P6,Fig.1.3) 德布罗依(de brolie L V,1892-1987)法国理论物理学家,最初从巴黎大学获得历史学学士学位。他 曾说道,“通过历史学考试后,我感到我对哲学和科学更感兴趣。”后来他转到巴黎大学并获理学博士学位。 他一生经历的大部分时间都奉献于教育事业。曾任巴黎大学教授,法兰西科学院院士,英国皇家学会会员, 美国全国科学院院士。1924 年首先把光具有“波粒二象性”的概念加以推广,提出微观粒子同时具有波动 性,称这种波为“物质波”,即德布罗依波,并建议用电子在晶体上的衍射来验证。1927 年物理学家戴维 逊和盖革首先用慢电子进行电子衍射实验,同时乔治、佩吉特、汤姆逊也独立用快电子完成了类似实验, 从而证实了德布罗依的预言。1929 年因其在电子的波动性质方面的工作而荣膺诺贝尔物理学奖。他的理论 工作奠定了电子显微镜和电子衍射技术基础。著有《量子理论》、《波动力学的研究导论》、《光的一种新理 论》、《波动力学的新解释》等。 Question 1:为什么说微观粒子有波粒二象性,而宏观粒子不具有波粒二象性? 对电子:其粒子性已知,求其波长: m=9.10×10-31kg,电场加速下,v=106 ~107 m·s -1 由 mv h λ = = ⋅ = × = ⋅ = × − − − − 10 m s , 7.36 10 m 10 m s , 7.36 10 m 7 1 9 6 1 10 λ λ 时 时 v v 这些波长都在 X 射线的波长范围内,通过晶体粉末时能产生衍射,得到衍射图象。 宏观物质的质量大,v 小,λ 就小;如对 10-7kg 的物体: v=10m·s -1,则λ =6.626×10-28 m。 没有任何仪器能够测出这样短的波长。 一些运动粒子的波长 物体粒子 m/kg v/m·s -1 λ /pm

西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 5 1V 电子 9.1×10-31 5.9×105 1 200 10 000V 电子 9.1×10-31 5.9×107 12 垒 球 2.0×10-1 30 1.1×10-22 枪 弹 1.0×10-2 1.0×103 6.6×10-23 从这里可以看出 h 的重要性,h 是个很小的值,m 接近于 h 时,λ 不能忽略;当 m>>h 时,因λ 很小,波动性失去了意义。 波粒二象性对化学的重要性在于:玻尔以波的微粒性(即能量量 子化概念)为基础建立了他的氢原子模型;薛定锷等以微粒波动性为 基础建立起原子的波动力学模型。 薛定谔(Schrodinger E, 1887-1961)奥地利物理学家,量子力学奠基人之一。出生于维也纳,并受教 于维也纳大学。历任德国、波兰和瑞士几所大学教授。自 1940 年 1956 年在爱尔兰都柏林高等研究院任教 授。其主要工作在数学物理学,特别是在原子物理学方面。在德布罗依的物质波理论的基础上,建立了波 动力学。由他所建立的薛定谔方程是量子力学中描述微观粒子(如电子等)运动状态的基本定律,在粒子 运动速度远小于光速的的条件下适用。它在量子力学中的地位大致相似于牛顿运动定律在经典力学中的地 位。因发展了原子理论,于 1933 年与狄拉克共获诺贝尔物理学奖。1944 年薛氏著有一部极有影响的著作 ——《生命是什么?》。 1.3 波尔模型(P19-P21) (1)连续光谱和线状光谱 a.光和电磁辐射 见图 1.1 b.氢原子光谱 见图 1.5 氢原子光谱特征:不连续的,线状的;有规律 Th l t ti
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 5 1V 电子 9.1×10-31 5.9×105 1 200 10 000V 电子 9.1×10-31 5.9×107 12 垒 球 2.0×10-1 30 1.1×10-22 枪 弹 1.0×10-2 1.0×103 6.6×10-23 从这里可以看出 h 的重要性,h 是个很小的值,m 接近于 h 时,λ 不能忽略;当 m>>h 时,因λ 很小,波动性失去了意义。 波粒二象性对化学的重要性在于:玻尔以波的微粒性(即能量量 子化概念)为基础建立了他的氢原子模型;薛定锷等以微粒波动性为 基础建立起原子的波动力学模型。 薛定谔(Schrodinger E, 1887-1961)奥地利物理学家,量子力学奠基人之一。出生于维也纳,并受教 于维也纳大学。历任德国、波兰和瑞士几所大学教授。自 1940 年 1956 年在爱尔兰都柏林高等研究院任教 授。其主要工作在数学物理学,特别是在原子物理学方面。在德布罗依的物质波理论的基础上,建立了波 动力学。由他所建立的薛定谔方程是量子力学中描述微观粒子(如电子等)运动状态的基本定律,在粒子 运动速度远小于光速的的条件下适用。它在量子力学中的地位大致相似于牛顿运动定律在经典力学中的地 位。因发展了原子理论,于 1933 年与狄拉克共获诺贝尔物理学奖。1944 年薛氏著有一部极有影响的著作 ——《生命是什么?》。 1.3 波尔模型(P19-P21) (1)连续光谱和线状光谱 a.光和电磁辐射 见图 1.1 b.氢原子光谱 见图 1.5 氢原子光谱特征:不连续的,线状的;有规律 Th l t ti

西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 6 s 1 2 1 3.289 10 1 2 2 15 − = × − n v s 1 1 3.289 10 1 2 2 2 1 15 − = × − n n v n=3,4,5,6 n2>n1 因此有里德堡方程式: = ∞ − 2 2 2 1 1 1 n n σ R (2)玻尔理论 玻尔理论的主要假设(P19) (a)核外电子只能在有确定半径和能量的轨道上(空态 stationary states)上运动, 且不辐射能量; (b)通常保持能量最低——基态(ground state) (c)获能量激发——激发态(excited state) (d)从激发态回到基态释放光能 hv = E2 − E1 E:轨道的能量 h E E v 2 − 1 = v:光的频率 h:Planck 常数 玻尔理论的成功之处: ·满意地解释了实验观察的氢原子光谱和类氢原子(He+ , Li2+, B3+)光谱,把 P9Fig.1.5 展开(出现能级 energy level): 波长数据来源 Hα Hβ Hγ Hδ 用玻尔理论的计算值/nm 656.2 486.1 434.0 410.1 实验测得值/nm 656.3 486.1 434.1 410.2 ·说明原子的稳定性; 对其他发光现象(如 X 光的形成)也能给予解释。 X 光:原子获得能量后,最内层 (K 层)的电子被激发跃迁到外层轨道,随后 L 层或 M 层的电子立即跳到 K 层空位,同时 以光子的形式放出能量。因能量大,λ 很小,不可见。 ·计算氢原子的电离能 电子由 n=1→n=∞,即电子脱离原子核的引力。 13.6 1 2 0 2 2 2 2 2 4 ∆ = ∞ − 1 = − = h k mz e E E E π e V (13.6×6.02×1023=1311.6 kJ·mol-1) 实验值 1312 kJ·mol-1
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 6 s 1 2 1 3.289 10 1 2 2 15 − = × − n v s 1 1 3.289 10 1 2 2 2 1 15 − = × − n n v n=3,4,5,6 n2>n1 因此有里德堡方程式: = ∞ − 2 2 2 1 1 1 n n σ R (2)玻尔理论 玻尔理论的主要假设(P19) (a)核外电子只能在有确定半径和能量的轨道上(空态 stationary states)上运动, 且不辐射能量; (b)通常保持能量最低——基态(ground state) (c)获能量激发——激发态(excited state) (d)从激发态回到基态释放光能 hv = E2 − E1 E:轨道的能量 h E E v 2 − 1 = v:光的频率 h:Planck 常数 玻尔理论的成功之处: ·满意地解释了实验观察的氢原子光谱和类氢原子(He+ , Li2+, B3+)光谱,把 P9Fig.1.5 展开(出现能级 energy level): 波长数据来源 Hα Hβ Hγ Hδ 用玻尔理论的计算值/nm 656.2 486.1 434.0 410.1 实验测得值/nm 656.3 486.1 434.1 410.2 ·说明原子的稳定性; 对其他发光现象(如 X 光的形成)也能给予解释。 X 光:原子获得能量后,最内层 (K 层)的电子被激发跃迁到外层轨道,随后 L 层或 M 层的电子立即跳到 K 层空位,同时 以光子的形式放出能量。因能量大,λ 很小,不可见。 ·计算氢原子的电离能 电子由 n=1→n=∞,即电子脱离原子核的引力。 13.6 1 2 0 2 2 2 2 2 4 ∆ = ∞ − 1 = − = h k mz e E E E π e V (13.6×6.02×1023=1311.6 kJ·mol-1) 实验值 1312 kJ·mol-1

西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 7 2 13.6 h E = − eV 那么,n=1, r1=52.9pm, E1=-13.6 eV n=2, r2=212pm, E2=-3.4 eV n=3, r3=477pm, E3=-1.5 eV M M n=∞ E∞=0 或者:v=3.289×1015 ∞ − 2 2 1 1 1 =3.289×1015 s -1 代入 E=hv=3.289×1015×6.626×10-34 =2.179×10-18(J) 再乘 6.02×10-23 得 1312 kJ·mol-1。 玻尔理论的局限性: ·不能解释精细结构(每条谱线是由二条紧邻的谱线组成) ·不能解释原子光谱在磁场中的分裂 ·不能解释多电子原子的光谱 玻尔(Bohr N H D, 1885-1962)丹麦原子物理学家。1885 年 10 月 7 日出生于哥本哈根,1911 年获物 理学博士学位。随后在剑桥大学卡文迪什实验室工作。1912 年在曼彻斯特卢瑟福实验室工作。1916 年任哥 本哈根大学物理学教授,1920-1956 年任该校理论物理研究所所长。1939-1962 年,任丹麦皇家科学院院长。 还曾为丹麦原子能委员会主席和许多国家的科学院名誉院士。 他的卓越贡献是 1913 年提出玻尔原子模型,成功地解释了氢原子光谱,圆满地解释了元素的周期性。 把化学推进到更深的层次,使物理和化学统一到量子理论的基础上来。该模型的提出,是原子结构理论发 展史上的一个里程碑。虽然原子的波动模型出现后,该模型已过时,但其结果在定性方面还是正确的。1939 年还提出原子核液滴模型,对理解裂变机理有很大帮助。 二次大战期间到美国参加原子弹研制工作。战后,致力于原子能的和平利用。因在研究原子结构和辐 射方面的贡献荣获 1922 年诺言贝尔物理学奖。发表论文 115 篇。主要著作有《原子学说与自然界的描述》 (1939)和《知识的统一性》(1955)。 1.4 波动力学模型——迄今最成功的原子结构模型 1.4.1 测不准原理和波动力学模型轨道概念的形成 a.uncertainty priciple(Heisenberg w) 可通俗地表达为:不可能同时测得电子的精确位置和动量(由于电子具有波粒二象 性) ∆x ⋅ ∆p ≈ h b.从理论上讲,任何运动物体(包括宏观物体)都得服从 Heigenberg principle,但只 有在处理微观世界的运动时,才显得不可忽视。 c.重要暗示:不可能存在 Ruther ford 和 Bohr 模型中行星绕太阳那样的电子轨道! d.重要提示:对于电子衍射的解释,即电子的波动性与微粒行为的统计规律相联系。 人们无法知道每个电子落在感光屏的哪个位置,但统计结果却能显示电子在不同区域出现的 机会,出现机会多(概率较大)的,区域内花纹较深,出现机会少(概率较小)的,区域内
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 7 2 13.6 h E = − eV 那么,n=1, r1=52.9pm, E1=-13.6 eV n=2, r2=212pm, E2=-3.4 eV n=3, r3=477pm, E3=-1.5 eV M M n=∞ E∞=0 或者:v=3.289×1015 ∞ − 2 2 1 1 1 =3.289×1015 s -1 代入 E=hv=3.289×1015×6.626×10-34 =2.179×10-18(J) 再乘 6.02×10-23 得 1312 kJ·mol-1。 玻尔理论的局限性: ·不能解释精细结构(每条谱线是由二条紧邻的谱线组成) ·不能解释原子光谱在磁场中的分裂 ·不能解释多电子原子的光谱 玻尔(Bohr N H D, 1885-1962)丹麦原子物理学家。1885 年 10 月 7 日出生于哥本哈根,1911 年获物 理学博士学位。随后在剑桥大学卡文迪什实验室工作。1912 年在曼彻斯特卢瑟福实验室工作。1916 年任哥 本哈根大学物理学教授,1920-1956 年任该校理论物理研究所所长。1939-1962 年,任丹麦皇家科学院院长。 还曾为丹麦原子能委员会主席和许多国家的科学院名誉院士。 他的卓越贡献是 1913 年提出玻尔原子模型,成功地解释了氢原子光谱,圆满地解释了元素的周期性。 把化学推进到更深的层次,使物理和化学统一到量子理论的基础上来。该模型的提出,是原子结构理论发 展史上的一个里程碑。虽然原子的波动模型出现后,该模型已过时,但其结果在定性方面还是正确的。1939 年还提出原子核液滴模型,对理解裂变机理有很大帮助。 二次大战期间到美国参加原子弹研制工作。战后,致力于原子能的和平利用。因在研究原子结构和辐 射方面的贡献荣获 1922 年诺言贝尔物理学奖。发表论文 115 篇。主要著作有《原子学说与自然界的描述》 (1939)和《知识的统一性》(1955)。 1.4 波动力学模型——迄今最成功的原子结构模型 1.4.1 测不准原理和波动力学模型轨道概念的形成 a.uncertainty priciple(Heisenberg w) 可通俗地表达为:不可能同时测得电子的精确位置和动量(由于电子具有波粒二象 性) ∆x ⋅ ∆p ≈ h b.从理论上讲,任何运动物体(包括宏观物体)都得服从 Heigenberg principle,但只 有在处理微观世界的运动时,才显得不可忽视。 c.重要暗示:不可能存在 Ruther ford 和 Bohr 模型中行星绕太阳那样的电子轨道! d.重要提示:对于电子衍射的解释,即电子的波动性与微粒行为的统计规律相联系。 人们无法知道每个电子落在感光屏的哪个位置,但统计结果却能显示电子在不同区域出现的 机会,出现机会多(概率较大)的,区域内花纹较深,出现机会少(概率较小)的,区域内

西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 8 花纹较浅。 从这个意义讲,实物的微粒波是概率波——性质上不同于光波的一种波, 1.4.2 描述电子运动状态的量子数 ·电子运动的状态服从 Schrodinger E 方程(奥地利物理学家,1926) ψ ψ ψ ψ π ( ) 8 2 2 2 2 2 2 2 2 E V h m x y z = − − ∂ ∂ + ∂ ∂ + ∂ ∂ 二阶偏微分方程 ψ 为描述特定微粒运动状态的波函数(wave functions),即电子在核外空间运动状态的 数学表达式,是空间坐标的函数。若确定了空间坐标,波函数也就有了一定的数值。绘出波 函数对空间坐标的图形,便能形象地反映出电子在核外空间运动状态。所以把一定量力化 条件下的波函数看作一个原子轨道(atomic orbitals)(与玻尔的轨道 orbit 不同)。 由于波强度大的地方,电子出现的几率也大,波的强度和|ψ | 2 成正比,则 |ψ | 2 ∝波的强度∝电子出现的几率。 综上讨论,核外电子运动状态的近代观点是: (1) 核外电子具有波粒二象性,它以确定的波函数形式在原子核外运动; (2)电子在原子核外空间有确定的几率分布。 ·求 Schrodinger 方程的解,就是求的描述微粒运动状态的波函数ψ 以及与该状态相对 应的能量 E。 ·解的ψ 不是一个具体数值,而是包括三个常数项(n,l,m)和三个变量(x,y,z)的函数 式,用 y=f(x) ψ n,l,m(x,y,z)表示。由于原子核具有球形对称的库仑场,人们更喜 欢用球坐标表示:ψ n,l,m(r,θ , ) ϕ 。 2 2 2 cos sin sin sin cos r x y z z r y r x r = + + = = = θ θ ϕ θ ϕ 变换后的 Schrodinger 方程为: ( ) 0 8 sin 1 sin sin 1 1 2 2 2 2 2 2 2 2 2 + − = ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ ϕ π ϕ ϕ θ θ ϕ θ θ θ ϕ E V h m r r r r r r 坐标变换后分离变量,即将一个含有三个变量的方程化成三个只含有一个变量的方程, 以便求解: 令ψ n,l,m(r, ,θ , )=R(r),Y( ϕ θ , )( ϕ 径向部分,角度部分) 再令 Y(θ ,ϕ )= ) Θ(θ )Φ(ϕ 即代入上式的三个只含一个变量的常微分方程 = Φ Φ− + = Θ + − = (3) 1 (sin ) sin (2) sin ( ) (1) 1 8 2 2 2 2 2 2 2 λ ϕ β θ γ θ θ θ θ β π d d d d d d E V h mr dr dR r dr d R n≠0,否则ψ(x) =0,不合理,也不能为分数,必须是量子化的。 为了保证解的合理性(或描述电子运动状态的合理性)需引入三个常数项(n,l,m),它
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 8 花纹较浅。 从这个意义讲,实物的微粒波是概率波——性质上不同于光波的一种波, 1.4.2 描述电子运动状态的量子数 ·电子运动的状态服从 Schrodinger E 方程(奥地利物理学家,1926) ψ ψ ψ ψ π ( ) 8 2 2 2 2 2 2 2 2 E V h m x y z = − − ∂ ∂ + ∂ ∂ + ∂ ∂ 二阶偏微分方程 ψ 为描述特定微粒运动状态的波函数(wave functions),即电子在核外空间运动状态的 数学表达式,是空间坐标的函数。若确定了空间坐标,波函数也就有了一定的数值。绘出波 函数对空间坐标的图形,便能形象地反映出电子在核外空间运动状态。所以把一定量力化 条件下的波函数看作一个原子轨道(atomic orbitals)(与玻尔的轨道 orbit 不同)。 由于波强度大的地方,电子出现的几率也大,波的强度和|ψ | 2 成正比,则 |ψ | 2 ∝波的强度∝电子出现的几率。 综上讨论,核外电子运动状态的近代观点是: (1) 核外电子具有波粒二象性,它以确定的波函数形式在原子核外运动; (2)电子在原子核外空间有确定的几率分布。 ·求 Schrodinger 方程的解,就是求的描述微粒运动状态的波函数ψ 以及与该状态相对 应的能量 E。 ·解的ψ 不是一个具体数值,而是包括三个常数项(n,l,m)和三个变量(x,y,z)的函数 式,用 y=f(x) ψ n,l,m(x,y,z)表示。由于原子核具有球形对称的库仑场,人们更喜 欢用球坐标表示:ψ n,l,m(r,θ , ) ϕ 。 2 2 2 cos sin sin sin cos r x y z z r y r x r = + + = = = θ θ ϕ θ ϕ 变换后的 Schrodinger 方程为: ( ) 0 8 sin 1 sin sin 1 1 2 2 2 2 2 2 2 2 2 + − = ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ ϕ π ϕ ϕ θ θ ϕ θ θ θ ϕ E V h m r r r r r r 坐标变换后分离变量,即将一个含有三个变量的方程化成三个只含有一个变量的方程, 以便求解: 令ψ n,l,m(r, ,θ , )=R(r),Y( ϕ θ , )( ϕ 径向部分,角度部分) 再令 Y(θ ,ϕ )= ) Θ(θ )Φ(ϕ 即代入上式的三个只含一个变量的常微分方程 = Φ Φ− + = Θ + − = (3) 1 (sin ) sin (2) sin ( ) (1) 1 8 2 2 2 2 2 2 2 λ ϕ β θ γ θ θ θ θ β π d d d d d d E V h mr dr dR r dr d R n≠0,否则ψ(x) =0,不合理,也不能为分数,必须是量子化的。 为了保证解的合理性(或描述电子运动状态的合理性)需引入三个常数项(n,l,m),它

西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 9 们只能按一定的规则取值,即三个量子数,与玻尔的量子数不同: 合理性: (1)ψ 必须是单值的,在空间任一点ψ 只能有一个值,否则|ψ 2 |值不只一个,显然不 可能。 (2)ψ 必须是有限的,否则|ψ | 2 是无限值,也不可能。 (3)ψ 必须是连续的,所有的波都是连续的。 (1)玻尔只用了一个量子数 n; (2)玻尔引入 n 是人为假定的。 ·四个量子数(见 P11-12) (1)主量子数(principal quantum number) n 符号 物理意义,取值范围: (2)角量子数(angula momentum quantum number)l 全称:轨道角动量量子数,直观地看作轨道形状的量子数,取值 0,1,2,3. (n-1),一个值对应一个亚层(subshell) (3)磁量子数(magnetic quantum number)m 原子轨道在空间的取向(角动量在空间的给定方向上的分量的大小)取值+l→0→ -l 间。 l 相同时,虽因 m 不同,原子轨道可能有不同的伸展方向,但并不影响电子的能量, 即 m 与能量无关。 等价轨道或简并轨道 (equivalent orbital) 简并态 degenerate state 简并度 degenracy 差别显示在外磁场存在下的光谱图上(Zeeman effect) 第 1 个电子 n=1, l=0, m=0, ms=+ 2 1 第 2 个电子 n=1, l=0, m=0, ms=- 2 1 (1,0,0, + 2 1 ) (1,0,0, - 2 1 ) (4)自旋量子数(Spin quantum number)ms 强磁场时光谱图上的每条谱线均由两条十分靠近的谱线组成,ms=± 2 1 ,用↑、↓表示
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 9 们只能按一定的规则取值,即三个量子数,与玻尔的量子数不同: 合理性: (1)ψ 必须是单值的,在空间任一点ψ 只能有一个值,否则|ψ 2 |值不只一个,显然不 可能。 (2)ψ 必须是有限的,否则|ψ | 2 是无限值,也不可能。 (3)ψ 必须是连续的,所有的波都是连续的。 (1)玻尔只用了一个量子数 n; (2)玻尔引入 n 是人为假定的。 ·四个量子数(见 P11-12) (1)主量子数(principal quantum number) n 符号 物理意义,取值范围: (2)角量子数(angula momentum quantum number)l 全称:轨道角动量量子数,直观地看作轨道形状的量子数,取值 0,1,2,3. (n-1),一个值对应一个亚层(subshell) (3)磁量子数(magnetic quantum number)m 原子轨道在空间的取向(角动量在空间的给定方向上的分量的大小)取值+l→0→ -l 间。 l 相同时,虽因 m 不同,原子轨道可能有不同的伸展方向,但并不影响电子的能量, 即 m 与能量无关。 等价轨道或简并轨道 (equivalent orbital) 简并态 degenerate state 简并度 degenracy 差别显示在外磁场存在下的光谱图上(Zeeman effect) 第 1 个电子 n=1, l=0, m=0, ms=+ 2 1 第 2 个电子 n=1, l=0, m=0, ms=- 2 1 (1,0,0, + 2 1 ) (1,0,0, - 2 1 ) (4)自旋量子数(Spin quantum number)ms 强磁场时光谱图上的每条谱线均由两条十分靠近的谱线组成,ms=± 2 1 ,用↑、↓表示

西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 10 注意:(1)量子力学原理包括: 原理 量子化 测不准原理 微观粒子的波粒二象性 Paali (2)解氢原子的 Schrodinger 方程只能得 n ,l ,m (3)四个量子数的取值和意义 四个量子数的取值和意义 量子数 可取值 意义 主量子数 n 1,2,3.n 正整数 (1) 确定电子的能量。 (2) 确定电子出现几率最大处离核的 距离 副量子数 l 每一个 n,可取 l 值为 0,1,2,.(n-1) (1) 确定原子轨道的形状。L 为 0,1,2, 3,.所对应的 s、p、d、f 电子 有一定的形状,见教材第 243 页图 9-12。 (2) 与 n 一起确定多电子原子的轨道能 量。 磁量子数 m 每一个 l,可取 m 值为 0,±1,±2,. ± l 确定原子轨道在空间的取向。 自旋量子数 ms 每一个 ms 可取 s 值为± 2 1 描述电子绕自轴旋转的状态。 核外电子运动 ms m l n 自旋运动 轨道运动 与一套量子数相对应(自然也各有 1 个能量 Ei) 轨道概念的图形描述 介绍波动力学模型的目的: a、从四个量子数→原子中电子排布 b、建立轨道形象化概念→理解化学键的形成及分子结构 ·波函数的图形描述 ( , , ) ( ) m ( , ) ψ n,l,m r θ ϕ = Rn,l r ⋅ rl, θ ϕ 径向分布函数(P13,图 1.7) 角度分布函数 ·电子云图象:物理意义更明确(P13~15) ψ ——微粒波的振幅 |ψ | 2 ——概率密度 电子云——|ψ | 2 的图象
西北大学精品课程·重点课程·学科核心课程 - 无机化学与化学分析 10 注意:(1)量子力学原理包括: 原理 量子化 测不准原理 微观粒子的波粒二象性 Paali (2)解氢原子的 Schrodinger 方程只能得 n ,l ,m (3)四个量子数的取值和意义 四个量子数的取值和意义 量子数 可取值 意义 主量子数 n 1,2,3.n 正整数 (1) 确定电子的能量。 (2) 确定电子出现几率最大处离核的 距离 副量子数 l 每一个 n,可取 l 值为 0,1,2,.(n-1) (1) 确定原子轨道的形状。L 为 0,1,2, 3,.所对应的 s、p、d、f 电子 有一定的形状,见教材第 243 页图 9-12。 (2) 与 n 一起确定多电子原子的轨道能 量。 磁量子数 m 每一个 l,可取 m 值为 0,±1,±2,. ± l 确定原子轨道在空间的取向。 自旋量子数 ms 每一个 ms 可取 s 值为± 2 1 描述电子绕自轴旋转的状态。 核外电子运动 ms m l n 自旋运动 轨道运动 与一套量子数相对应(自然也各有 1 个能量 Ei) 轨道概念的图形描述 介绍波动力学模型的目的: a、从四个量子数→原子中电子排布 b、建立轨道形象化概念→理解化学键的形成及分子结构 ·波函数的图形描述 ( , , ) ( ) m ( , ) ψ n,l,m r θ ϕ = Rn,l r ⋅ rl, θ ϕ 径向分布函数(P13,图 1.7) 角度分布函数 ·电子云图象:物理意义更明确(P13~15) ψ ——微粒波的振幅 |ψ | 2 ——概率密度 电子云——|ψ | 2 的图象