
第一章 概率论的基本概念 P&S §1随机事件的概率 目录索引 随机事件 二事件间的关系与运算 三 频率与概率 合】返回主目录
一 随 机 事 件 二 事件间的关系与运算 三 频 率 与 概 率 §1 随 机 事 件 的 概率 目录索引 第一章 概率论的基本概念 返回主目录

第一章 概率论的基本概念 随机事件 在生活当中,经常接触到事件的概率, 比如:隆水概率为30%, 某强队对弱队赢球的概率为80% 某个固定群体中男女比例为54:46; 这种在个别实验中其结果呈现出不确定性; 在大量重复实验中其结果又具有统计规律性的现象, 我们称之为随机现象,概率论与数理统计是研究和 揭示随机现象统计规律性的一门学科。 合】返回主目录
我们称之为随机现象,概率论与数理统计是研究和 揭示随机现象统计规律性的一门学科。 一 、 随 机 事 件 比如: 降水 概率为 30% , 某强队对弱队 赢球 的概率为 80% , 某个固定群体中 男女比例 为 54:46 ; 在生活当中,经常接触到事件的概率, 这种在个别实验中其结果呈现出不确定性; 在大量重复实验中其结果又具有统计规律性的现象, 第一章 概率论的基本概念 返回主目录

第一章 概率论的基本概念 随机试验(Experiment) 这里试验的含义十分广泛,它包括各种各样 的科学实验,也包括对事物的某一特征的观察。 其典型的例子有: E1:抛一枚硬币,观察正面H(Heads)、反面T (Tails)出现的情况。 E2:将一枚硬币抛掷三次,观察正面、反面出现 的情况。 E3:将一枚硬币抛掷三次,观察出现正面的次数。 E4:抛一颗骰子,观察出现的点数。 合】返回主目录
E1:抛一枚硬币,观察正面H(Heads)、反面T (Tails)出现的情况。 E2 :将一枚硬币抛掷三次,观察正面、反面出现 的情况。 E3:将一枚硬币抛掷三次,观察出现正面的次数。 E4:抛一颗骰子,观察出现的点数。 这里试验的含义十分广泛,它包括各种各样 的科学实验,也包括对事物的某一特征的观察。 其典型的例子有: 随机试验(Experiment ) 第一章 概率论的基本概念 返回主目录

第一章 概率论的基本概念 有儿式金险 E5:记录寻呼台一分钟内接到的呼唤次数。 E6:在一批灯泡中任意抽取一只,测试它的寿命。 E:记录某地一昼夜的最高温度和最高温度。 这些实验具有以下特点: •可以在相同的条件下重复进行: 每次实验的可能结果不止一个,并且能事先明确 实验的所有可能结果; •进行一次实验之前不能确定哪一个结果会出现。 合】返回主目录
E5:记录寻呼台一分钟内接到的呼唤次数。 E6:在一批灯泡中任意抽取一只,测试它的寿命。 E7:记录某地一昼夜的最高温度和最高温度。 这些实验具有以下特点: •可以在相同的条件下重复进行; •每次实验的可能结果不止一个,并且能事先明确 实验的所有可能结果; •进行一次实验之前不能确定哪一个结果会出现。 第一章 概率论的基本概念 返回主目录

第一章 概率论的基本慨念 样本空间(Space) 定义 将随机试验E的所有可能结果组成的集合 称为E的样本空间,记为S。样本空间的 元素,即E的每个结果,称为样本点。 S1:{H,T} S2:HHH,HHT,HTH,THH, HTT,THT,TTH,TTT S3:{0,1,2,3} S4:{1,2,3,4,5,6} 合】返回主目录
样本空间(Space) 定义 将随机试验 E 的所有可能结果组成的集合 称为 E 的样本空间, 记为 S 。样本空间的 元素,即 E 的每个结果,称为样本点。 S1 : { H , T } S2 : { HHH, HHT, HTH, THH, HTT, THT, TTH, TTT } S3 : { 0, 1, 2, 3 } S4 : { 1, 2, 3, 4, 5, 6 } 第一章 概率论的基本概念 返回主目录

第一章 概率论的基本概念 E:记录寻呼台一分钟内接到的呼唤次数。 E。:在一批灯泡中任意抽取一只,测试它的寿命。 E7:记录某地一昼夜的最高温度和最高温度。 S5:{0,1,23.} S6:{t|t≥0} S2:{(x,y)|T≤x,y≤T1} 合】返回主目录
S5 : {0,1,2,3.} S6 : { t | t 0 } S7 : { ( x , y ) | T 0 x , y T1 } E5:记录寻呼台一分钟内接到的呼唤次数。 E6:在一批灯泡中任意抽取一只,测试它的寿命。 E7:记录某地一昼夜的最高温度和最高温度。 第一章 概率论的基本概念 返回主目录

第一章 概率论的基本慨念 随机事件 定义: •随机事件:称试验E的样本空间S的子集为E的 随机事件; •基本事件:有一个样本点组成的单点集; •必然事件:样本空间S本身: ·不可能事件:空集⑦。 我们称一个随机事件发生当且仅当它所包 含的一个样本点在试验中出现. 合返回主目录
定义: •随机事件 : 称试验 E 的样本空间 S 的子集为 E 的 随机事件; •基本事件 : 有一个样本点组成的单点集; •必然事件 : 样本空间 S 本身; •不可能事件 : 空集。 随 机 事 件 我们称一个随机事件发生当且仅当它所包 含的一个样本点在试验中出现. 第一章 概率论的基本概念 返回主目录

第一章 概率论的基本概念 例如:S2中事件A={HHH,HHT,HTH,HTT} 表示“第一次出现的是正面” S6中事件B={t<1000} 表示“灯泡是次品” 事件B2={tt≥1000} 表示“灯泡是合格品” 事件B3={≥1500 表示“灯泡是一级品” 合】返回主目录
例如:S2 中事件 A={HHH,HHT,HTH,HTT} 表示 “第一次出现的是正面” S6 中事件 B1={t|t1000} 表示 “灯泡是次品” 事件 B2={t|t 1000} 表示 “灯泡是合格品” 事件 B3={t|t1500} 表示“灯泡是一级品” 第一章 概率论的基本概念 返回主目录

第一章概率论的基本慨念 事件间的关系与运算 10包含关系AcB 20和事件 AU B 30 积事件 A∩B 40差事件 A-B 50 互不相容 A0B=0 60 对立事件A∩B=0 AU B=S 合】返回主目录
1 0 包含关系 二 、 事件间的关系与运算 2 0 和事件 3 0 积事件 4 0 差事件 5 0 互不相容 6 0 对立事件 S A B A B A B A B A − B A B = A B S A B = = 第一章 概率论的基本概念 返回主目录
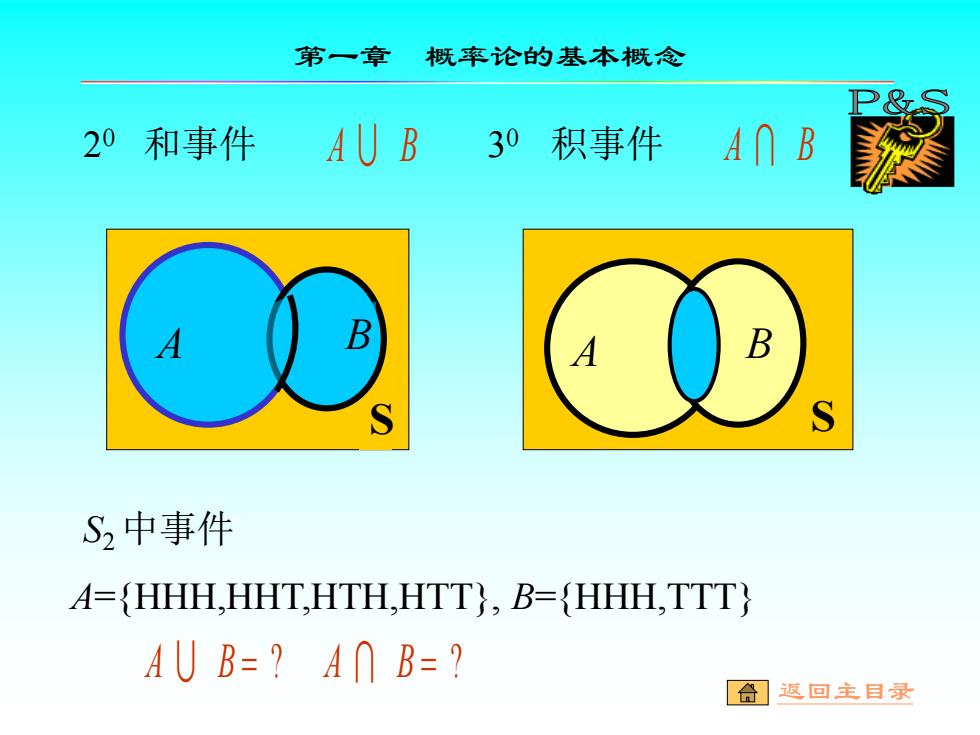
第一章 概率论的基本概念 20和事件 AU B 3 30积事件 A∩B B S2中事件 4=HHH,HHT,HTH,HTT,B=HHH,TTT AUB=?A∩B=? 合】返回主目录
S A B S2 中事件 A={HHH,HHT,HTH,HTT}, B={HHH,TTT} 2 0 和事件 3 A B 0 积事件 A B A B = ? A B = ? 第一章 概率论的基本概念 S A B 返回主目录