
§6.4正态总体 6.4.1x2分布 它是由正态分布派生出来的一种分布。 定义1:设X,X,.,X相互独立,且均 服从正态分布NO,1),则称随机变量 X2=X+X,2++X 服从自由度为n的卡方分布,记成x
§6.4 正态总体 6.4.1 χ 2分布 它是由正态分布派生出来的一种分布。 定义1: 设 X1 , X2 , . , Xn 相互独立,且均 服从正态分布 N(0, 1), 则称随机变量 2 2 2 2 1 2 = X + X ++ Xn 服从自由度为 n 的卡方分布,记成 。 2 n χ

x分布的密度函数为 2 -x2 e x≥0, 0 x0 来定义。 @四的
2 n 分布的密度函数为 = − − 0, 0. , 0, 2 ( 2) 1 ( ; ) 2 1 2 2 x x e x n f x n n x n 其中Γ()为伽玛(Gamma)函数, 通过积分 来定义。 ( ) , 0 0 1 = − − x e d x x

由X分布的定义,不难得到其如下性质: (1).设X,X2,.,Xn独立同分布,且共同分布为 N(4,σ2),则 。三X-w-z2 (2).设y~,Y,~x,且二者相互独立,则 Y+Y~ 性质2称为2x2分布的可加性
2 由 分布的定义,不难得到其如下性质: ; 则 设 独立同分布,且共同分布为 ( ) ~ 1 ( , ), (1). , , , 2 1 2 2 2 1 2 n n i i n X N X X X = − ~ . (2). ~ ~ 2 1 2 2 2 2 1 n n n m Y Y Y Y + + 设 , ,且二者相互独立,则 性质2称为 2 分布的可加性

(3).若X~x,则E(X)=n,Var(X)=2n 进一步,由中心极限定理可以推出,n充 X-n 分大时,2n 近似于标准正态分布N(0,1)。 @四的
进一步,由中心极限定理可以推出, n 充 分大时, n X n 2 − 近似于标准正态分布N(0,1)。 (3). ~ ( ) Var( ) 2 . 2 若 X n ,则E X = n , X = n
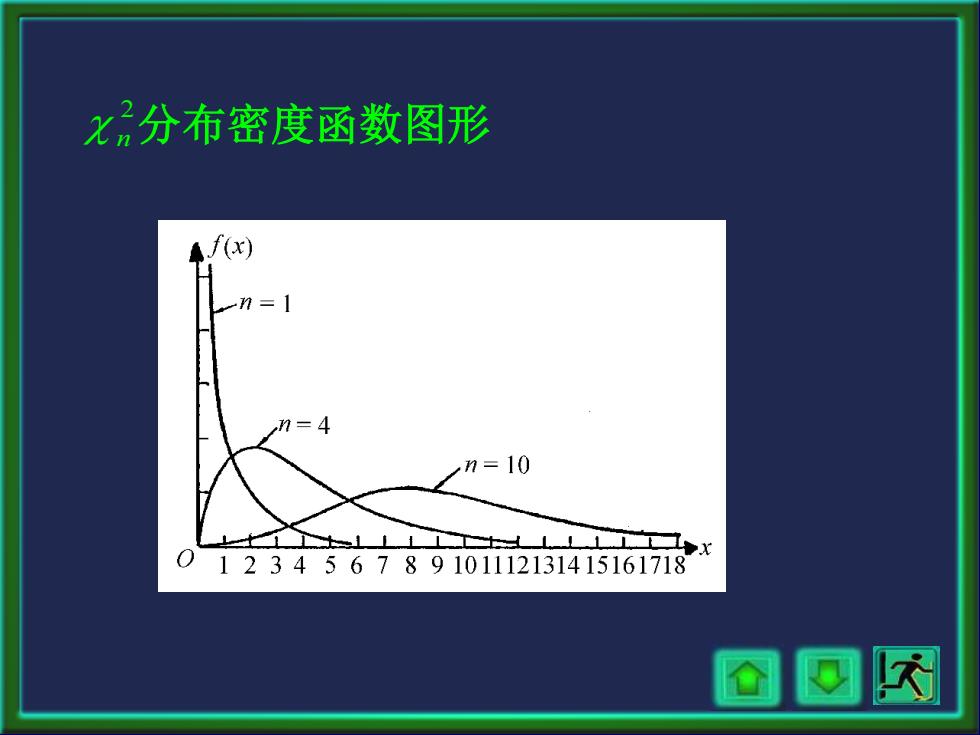
x分布密度函数图形 f(x) n= ,n=4 n=10 0123456789101112131415161718 @回冈
分布密度函数图形 2 n
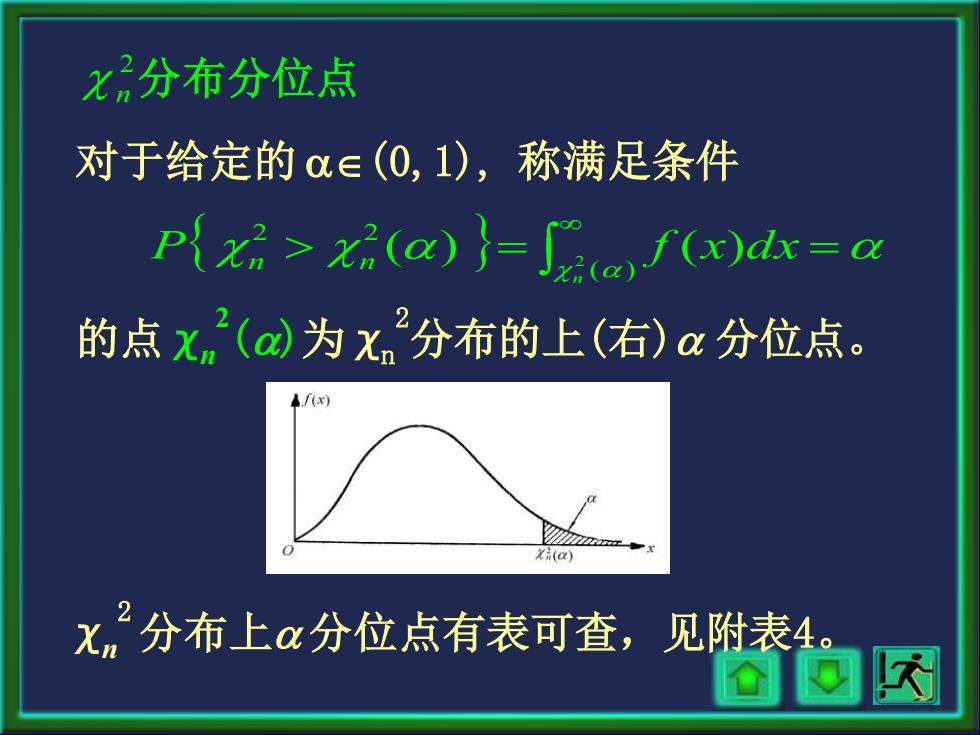
x分布分位点 对于给定的c∈(0,1),称满足条件 p{(a)=Sif(x)dx=a 的点x(a为X,分布的上(右)a分位点。 ◆./(x) Xi(a) Xm分布上a分位点有表可查,见附表4
χn 2分布上 分位点有表可查,见附表4。 对于给定的 (0,1), 称满足条件 = = ( ) 2 2 ( ) 2 ( ) n P n n f x d x 的点 χn 2 ()为 χn 2分布的上(右) 分位点。 n 2 分布分位点

6.4.2t分布 定义2:设X~N0,1),Y>xn2,且X与Y 相互独立,则称随机变量 X Yin 为服从自由度n的t分布,记为T一tn。 t分布的概率密度为 n+ -0<X<0
t分布的概率密度为 1 , . ( 2) ( 1) 2 ( ; ) 2 1 2 − + + = + − x n x n n n f x n n 为服从自由度 n 的 t 分布,记为 T ~ tn。 6.4.2 t 分布 Y n X T = 定义2: 设 X ~N(0, 1) , Y ~χn 2 , 且 X与Y 相互独立,则称随机变量
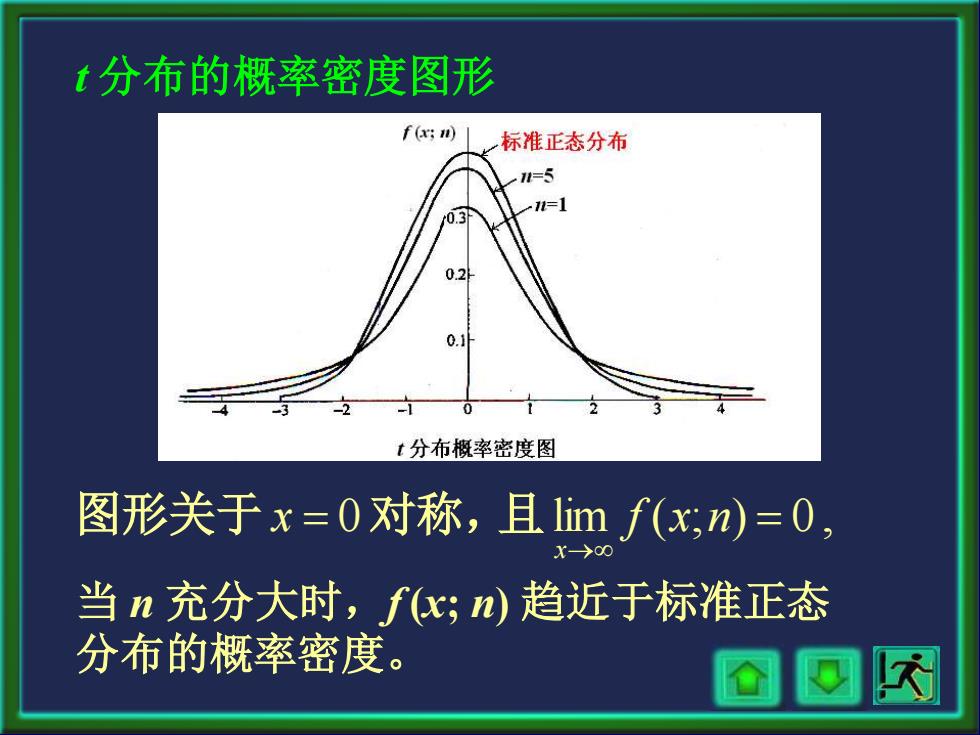
t分布的概率密度图形 f(x;n) 标准正态分布 =5 =] 0.3 0.2 t分布概率密度图 图形关于x=0对称,且1limf(x,n)=0, X→00 当n充分大时,fx;n)趋近于标准正态 分布的概率密度
t 分布的概率密度图形 当 n 充分大时,f (x; n) 趋近于标准正态 分布的概率密度。 = 0 lim ( ; ) = 0 , → x f x n x 图形关于 对称,且

数学期望与方差 不存在,n=1, E,)F0, n=2,3,.; Var(L,)= 不存在,n=1,2 n/(n-2),n=3,4,. @@风
数学期望与方差 − = = = = = = /( 2) n 3, 4, . n 1, 2, ( ) 0 2, 3, 1 ( ) , 不存在, , ; 不存在, , n n Var t n n E t n n
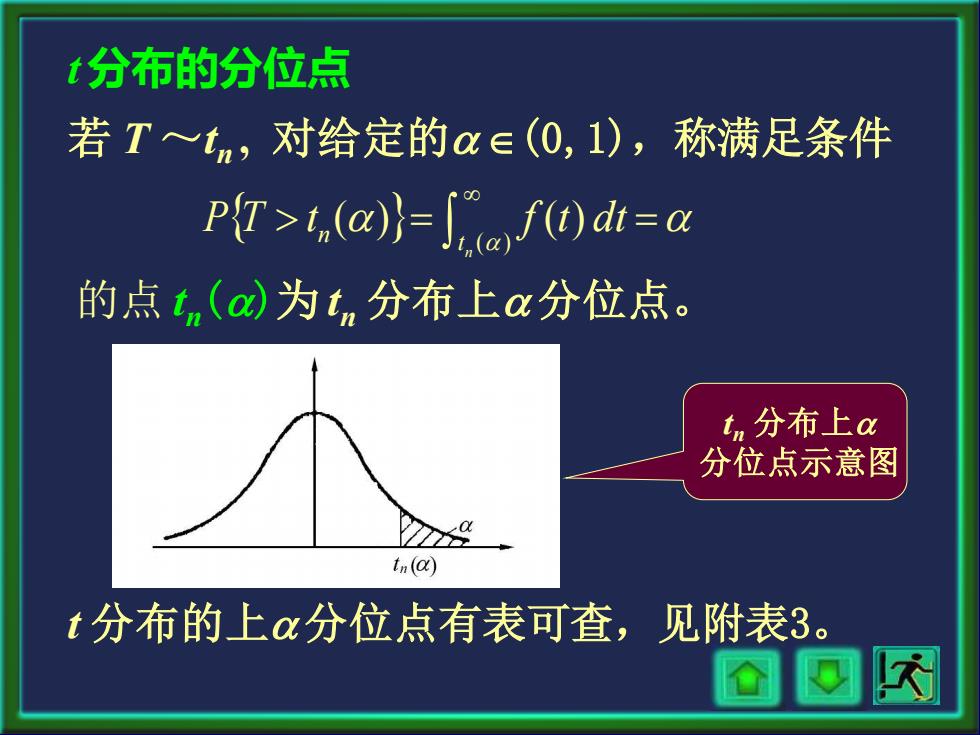
t分布的分位点 若T~tn,对给定的a∈(0,1),称满足条件 PT>i,(a)=f()di=a 的点tn(a为tn分布上x分位点。 tn分布上a 分位点示意图 in(a) t分布的上a分位点有表可查,见附表3
若 T ~tn , 对给定的 (0,1),称满足条件 t分布的分位点 的点 tn()为 tn 分布上 分位点。 = = ( ) ( ) ( ) n t n P T t f t dt t 分布的上分位点有表可查,见附表3。 tn 分布上 分位点示意图