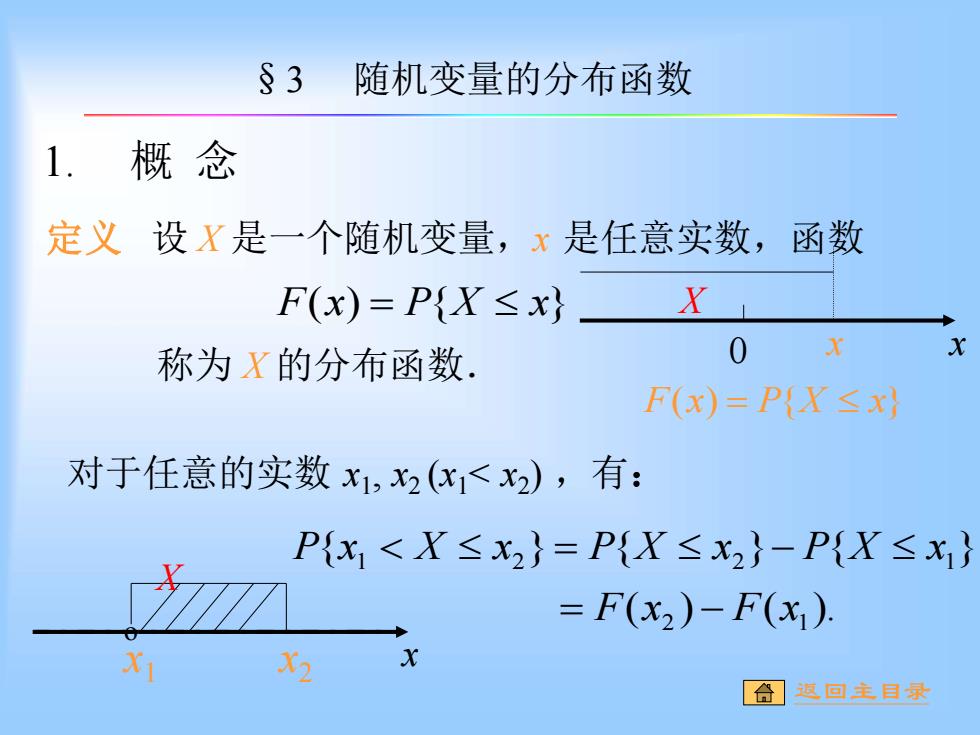
§3 随机变量的分布函数 1.概念 定义设X是一个随机变量,x是任意实数,函数 F(x)=P{X≤x} X 称为X的分布函数 0 Fx)=P{X≤x 对于任意的实数x1,2(x1<x2),有: P{x1<X≤x2}=P{X≤x2}-P{X≤x1} =F(x2)-F(x) X1 [合速回主自最
1. 概 念 定义 设 X 是一个随机变量,x 是任意实数,函数 F(x) = P{X x} 称为 X 的分布函数. 对于任意的实数 x1 , x2 (x1< x2 ) ,有: ( ) ( ). { } { } { } 2 1 1 2 2 1 F x F x P x X x P X x P X x = − = − x1 x2 x X o F(x) = P{X x} 0 x x X §3 随机变量的分布函数 返回主目录

§3随机变量的分布函数 2.例子 X-1 2 3 例1设随机变量X的分布律 为:求X的分布函数. P 4 4 解:当x<1时,满足X≤x的X的集合为⑦, F(x)=P{X≤x}=P{O}=0. X X-1023 合】这回主目
例 1 设随机变量 X 的分布律 为: 求 X 的分布函数. X pk 2 1 -1 2 3 4 1 4 1 解:当 x <-1 时,满足 X x的 X 的集合为, 0 2 x X x -1 3 F(x) = P{X x} = P{} = 0. 2. 例 子 §3 随机变量的分布函数 返回主目录
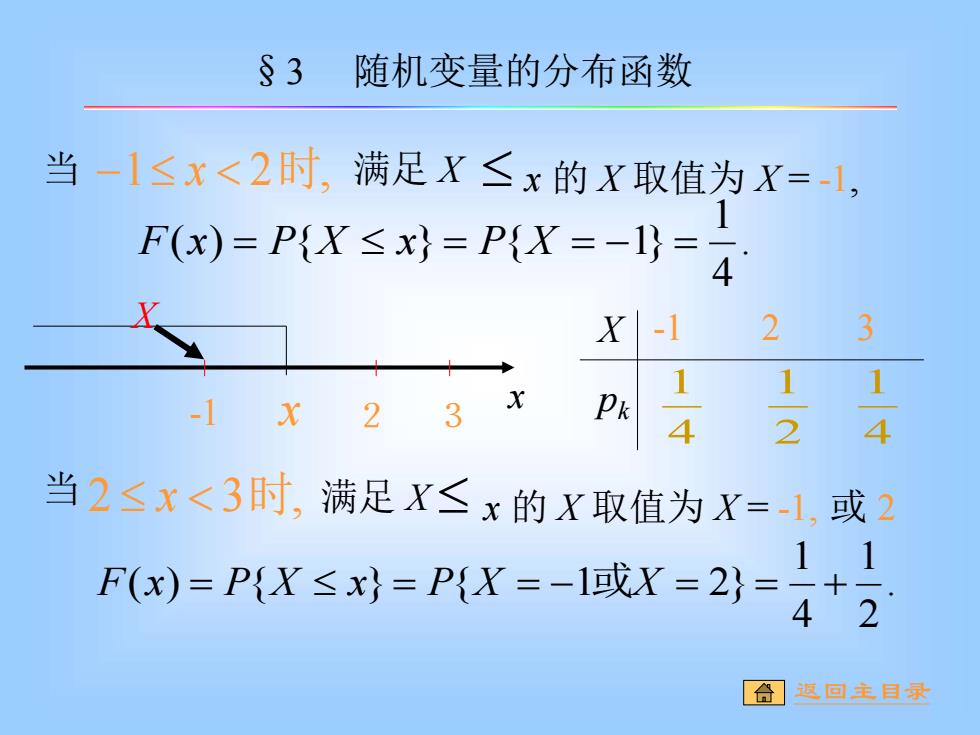
§3 随机变量的分布函数 当-1≤X<2时,满足X≤x的X取值为X=-1, FN=PX≤xy=PX=-l=4 X-1 23 1 1 1 23x Pk 4 2 4 当2≤X<3时,满足X≤x的X取值为X=-1,或2 F(N=PX≤x=PX=-l或X=2y=4+2 11 [合遵回主自零
当 −1 x 2时, 满足 X x 的 X 取值为 X = -1, . 4 1 F(x) = P{X x} = P{X = −1} = 2 x X -1 x 3 当 2 x 3时, 满足 X x 的 X 取值为 X = -1, 或 2 . 2 1 4 1 F(x) = P{X x} = P{X = −1或X = 2} = + X pk 2 1 -1 2 3 4 1 4 1 §3 随机变量的分布函数 返回主目录

§3 随机变量的分布函数 同理当3≤x时, F(x)=P{X≤x}=P{X=-1或X=2或X=3}=1. x<-1, F(x)= -1≤x<2, 3 4 2≤x<3, x≥3. 合这回主目是
同理当 3 x 时, F(x) = P{X x}= P{X = −1或X = 2或X = 3}=1. − − = 1, 3. , 2 3, 4 3 , 1 2, 4 1 0, 1, ( ) x x x x F x -1 0 1 2 3 x 1 §3 随机变量的分布函数 返回主目录
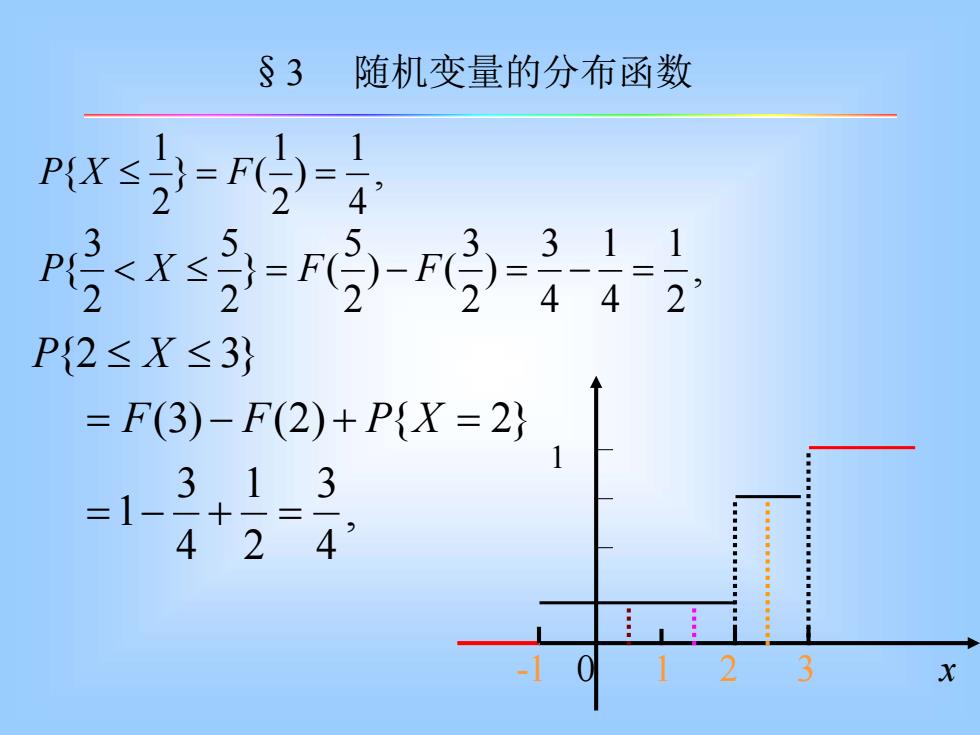
§3 随机变量的分布函数 PX≤=r=4 x P2≤X≤3} =F(3)-F2)+PX=2, -1-313 424?
, 4 1 ) 2 1 } ( 2 1 P{X = F = , 2 1 4 1 4 3 ) 2 3 ) ( 2 5 } ( 2 5 2 3 P{ X = F − F = − = , 4 3 2 1 4 3 1 (3) (2) { 2} {2 3} = − + = = − + = F F P X P X -1 0 1 2 3 x 1 §3 随机变量的分布函数
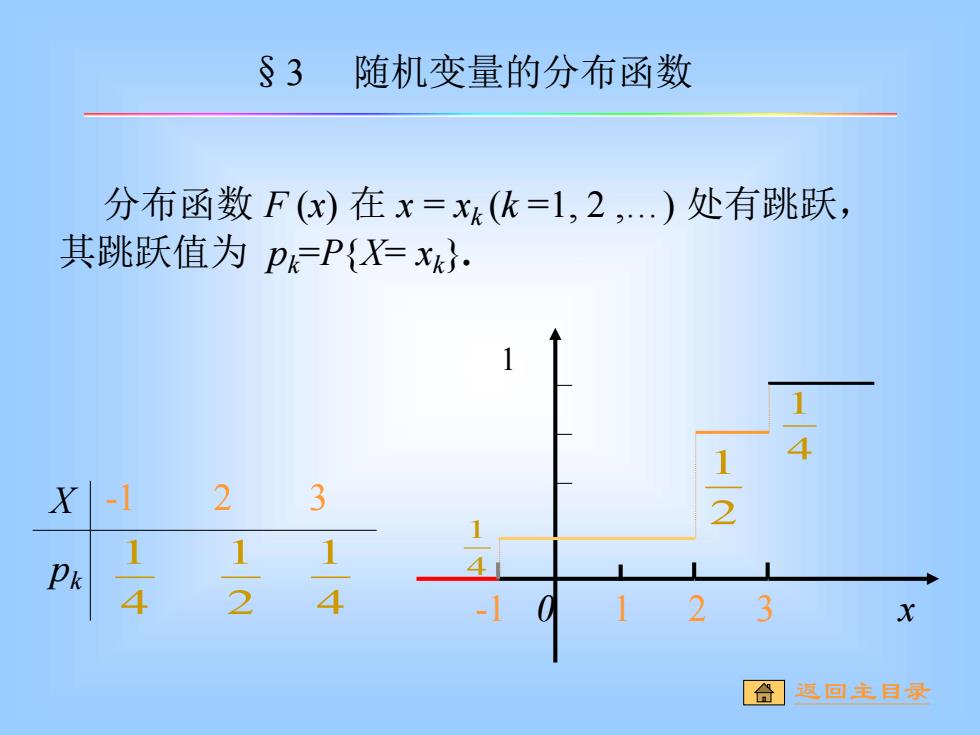
§3 随机变量的分布函数 分布函数F(x)在x=x(k=1,2,)处有跳跃, 其跳跃值为PP{X=xk: 1 4 X-1 2 3 2 1 Pk 14 2 4 2 3 合这回主目起
-1 0 1 2 3 x 1 2 1 4 1 4 1 分布函数 F (x) 在 x = xk (k =1, 2 ,.) 处有跳跃, 其跳跃值为 pk=P{X= xk}. X pk 2 1 -1 2 3 4 1 4 1 §3 随机变量的分布函数 返回主目录
§3 随机变量的分布函数 例2一个靶子是半径为2米的圆盘,设击中靶上 任一同心圆盘上的点的概率与该圆盘的面积成正比, 并设射击都能中靶,以X表示弹着点与圆心的距离. 试求随机变量X的分布函数. 解:(1)若x<0,则{X≤x)是不可能事件,于是 F(x)=P{X≤x}=P(O)=0. (2)若0≤x≤2,由题意, P{0≤X≤x}=kx2
例 2 一个靶子是半径为 2 米的圆盘,设击中靶上 任一同心圆盘上的点的概率与该圆盘的面积成正比, 并设射击都能中靶,以 X 表示弹着点与圆心的距离. 试求随机变量X的分布函数. 解:(1) 若 x < 0, 则 {X x} 是不可能事件,于是 F(x) = P{X x} = P() = 0. (2) {0 } , 0 2, 2 P X x k x x = 若 由题意, X §3 随机变量的分布函数

§3 随机变量的分布函数 取x=2,由已知得P0≤x≤2}=1,与上式对比 得k=114,即P0≤x≤2)=4 于是,0≤x≤2时 F(X)=P{X≤x}=P{X<O}+P{0≤X≤x} x2 4 (3)若x≥2,则{X≤x是必然事件,于是 F(x)=P{X≤x}=1. 合】这回主目
于是,0 x 2时 . 4 ( ) { } { 0} {0 } 2 x F X P X x P X P X x = = = + (3) 若 x 2 , 则 {X x} 是必然事件,于是 F(x) = P{X x} =1. . 4 1/ 4, {0 2} 2 x 得k = 即P x = 取x = 2,由已知得P{0 x 2}=1,与上式对比 §3 随机变量的分布函数 返回主目录
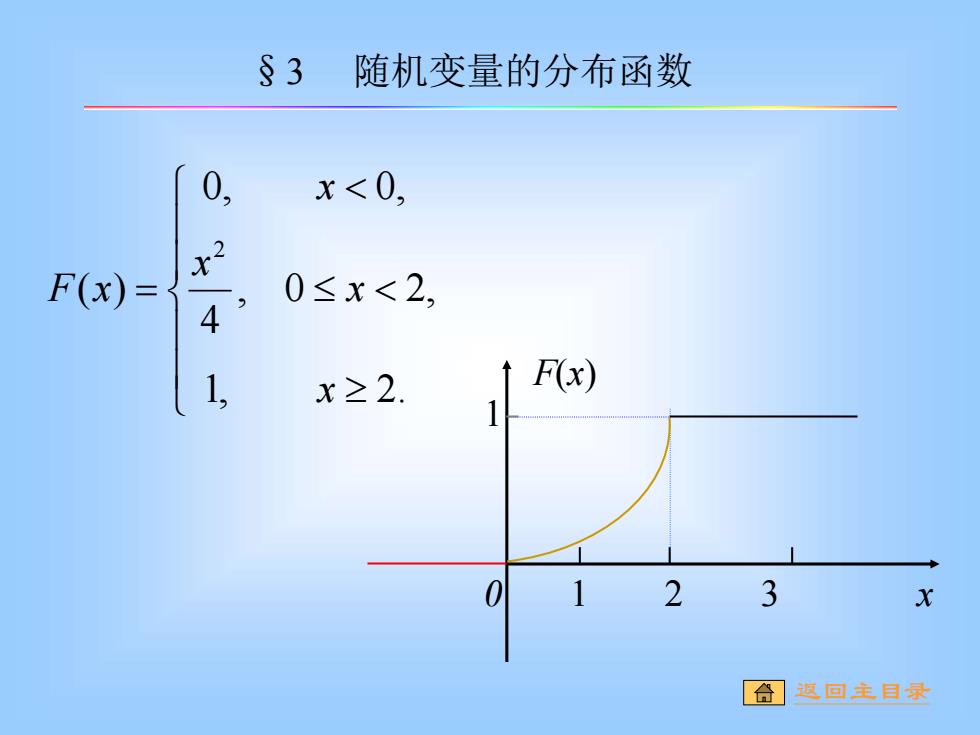
§3 随机变量的分布函数 0, x<0, F(x)=了 4 0≤x<2, 1, x≥2. F(x) 23 合遵回主自最
= 1, 2. , 0 2, 4 0, 0, ( ) 2 x x x x F x 0 1 2 3 1 F(x) x §3 随机变量的分布函数 返回主目录
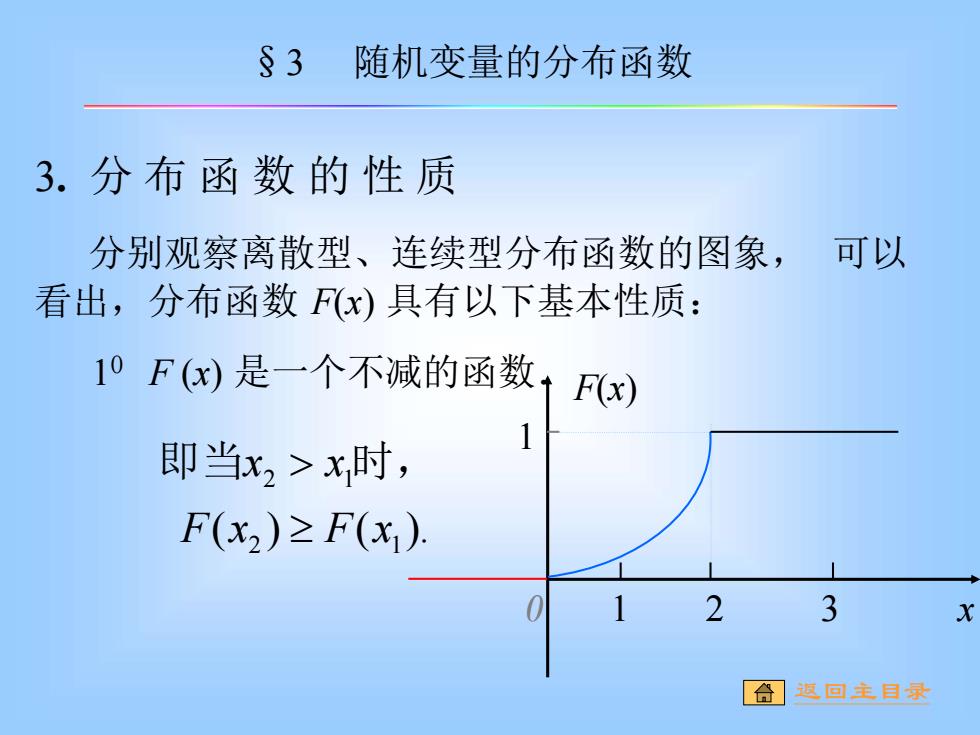
§3 随机变量的分布函数 3.分布函数的性质 分别观察离散型、连续型分布函数的图象,可以 看出,分布函数Fx)具有以下基本性质: 10F()是一个不减的函数1F) 即当x2>x时, F(x2)≥F(x). 2 3 合巡回主目暴
3. 分 布 函 数 的 性 质 分别观察离散型、连续型分布函数的图象, 可以 看出,分布函数 F(x) 具有以下基本性质: ( ) ( ). 2 1 2 1 F x F x x x 即当 时, 1 0 F (x) 是一个不减的函数. 0 1 2 3 1 F(x) x §3 随机变量的分布函数 返回主目录