新疆大学：《概率与数理统计》课程授课教案（PPT教学课件）第三章 随机变量及其分布 第5节 多维随机变量函数的分布

第三章 随机变量及其分布 一.和的分布 §5多维随机变量函数的分布 例1 设二维离散型随机变量(X,Y)的联合分布律为 2 3 4 X 4 0 0 0 2 18 名 0 0 3 0 4 6 6 6 令：Z=X+Y,试求随机变量Z的分布律 合返回主目录

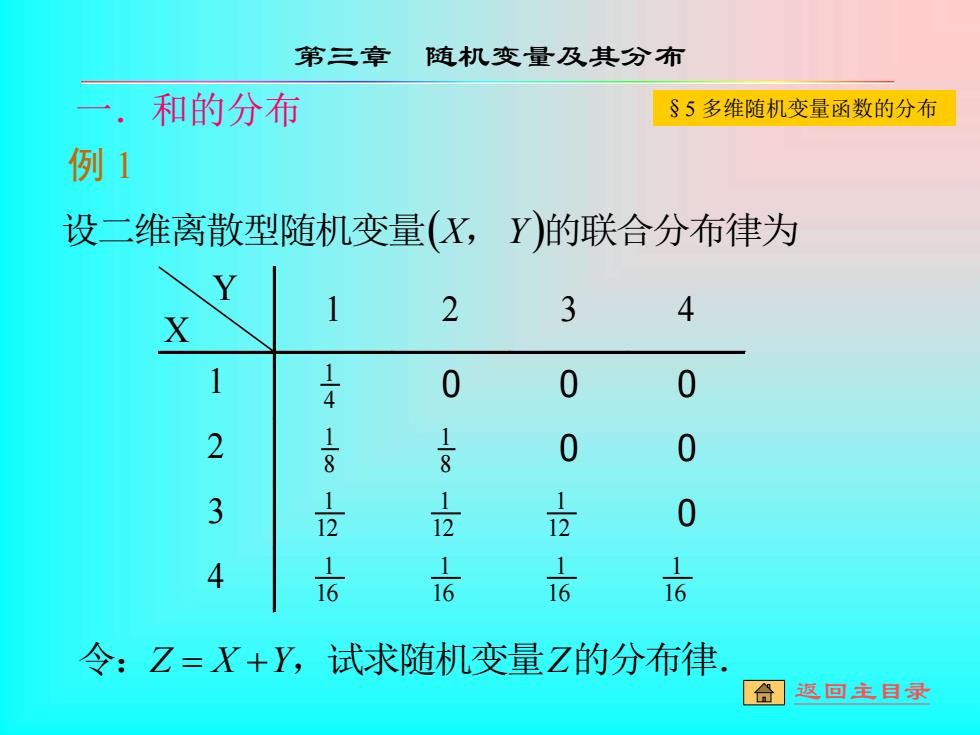
一．和的分布 第三章 随机变量及其分布 §5 多维随机变量函数的分布 例 1 Y X 1 2 3 4 1 4 1 0 0 0 2 8 1 8 1 0 0 3 12 1 12 1 12 1 0 4 16 1 16 1 16 1 16 1 设二维离散型随机变量(X，Y)的联合分布律为 令：Z = X +Y，试求随机变量Z的分布律． 返回主目录

第三章随机变量及其分布 例1（续） §5多维随机变量函数的分布 解： 由于X与Y的取值都是1,2,3,4， 可知随机变量Z=X+Y的取值为2,3,4,5,6,7,8. P2-=2-=PK=y- ,11 P{Z=3}=PX=1,Y=2+P{X=2,Y=1}=0+。 '88 P{Z=4}》 =P{X=1,Y=3}+P{X=2,Y=2+P{X-3,Y=1} .115 =0+二+ 81224 合】返回主目录

例 1（续） 解： 可知随机变量Z = X +Y的取值为2，3， 4，5， 6， 7，8． 由于X 与Y的取值都是1， 2，3， 4， PZ = 2= PX =1，Y =1 ； 4 1 = PZ = 3= PX =1，Y = 2+ PX = 2，Y =1 ； 8 1 8 1 = 0 + = PZ = 4 = PX =1，Y = 3+ PX = 2，Y = 2+ PX = 3，Y =1 ； 24 5 12 1 8 1 = 0 + + = 第三章 随机变量及其分布 §5 多维随机变量函数的分布 返回主目录

第三章随机变量及其分布 例1（续） §5多维随机变量函数的分布 P{Z=5} = P{X=1,Y=4}+P{X=2,Y=3} +P{X=3,Y=2+P{X=4,Y=1} =0+0+1+17 121648 P{Z=6} =P{X=2,Y=4+P{X=3,Y=3+P{X=4,Y=2} 117 =0+ 1216481 PZ=7}=PX=3,Y=4+PX=4,y=3}=0+= 1616 合返回主目录

例 1（续） PZ = 7 = PX = 3，Y = 4+ PX = 4，Y = 3 ； 16 1 16 1 = 0 + = PZ = 6 = PX = 2，Y = 4+ PX = 3，Y = 3+ PX = 4，Y = 2 ； 48 7 16 1 12 1 = 0 + + = PZ = 5      3 2  4 1 1 4 2 3 + = = + = = = = = + = = P X Y P X Y P X Y P X Y ， ， ， ， ； 48 7 16 1 12 1 = 0 + 0 + + = 第三章 随机变量及其分布 §5 多维随机变量函数的分布 返回主目录

第三章 随机变量及其分布 例1（续） §5多维随机变量函数的分布 P2=8=PX=4,y=46 由此得Z=X+Y的分布律为 2345678 P4令舞锅衣6名 合返回主目录

例 1（续） 由此得Z = X +Y的分布律为 PZ = 8 = PX = 4，Y = 4 ． 16 1 = Z 2 3 4 5 6 7 8 P 4 1 8 1 24 5 48 7 48 7 16 1 16 1 第三章 随机变量及其分布 §5 多维随机变量函数的分布 返回主目录

第三章 随机变量及其分布 例2 §5多维随机变量函数的分布 设随机变量X与Y相互独立，且分别服从参数为 元，与，的Poisson分布，令Z=X+Y,试求随 机变量Z的分布律. 解： 由随机变量X与Y的取值都是0,12，.， 可知随机变量Z=X+Y的取值也是0,1,2，.， 而且， P(Z=m)=P(X+Y=n)-PU(X=k.Y-n-A) 合返回主目录

例 2 机变量 的分布律． 与 的 分布，令 ，试求随 设随机变量 与 相互独立，且分别服从参数为 Z Z X Y X Y  1  2 Poisson = + 解：由随机变量X 与Y的取值都是0，1， 2，， 可知随机变量Z = X +Y的取值也是0，1， 2，， 而且， PZ = n= PX +Y = n 第三章 随机变量及其分布 §5 多维随机变量函数的分布 返回主目录 ( )       = = = − =  n k P X k Y n k 0

第三章 随机变量及其分布 例2（续） §5多维随机变量函数的分布 =>p(X=k,Y=n-k} k=0 -ΣPX-kPY=n-k} (随机变量X与Y的独立性 k=0 e - (n-k) =e2sn-y n! 名eA n 合返回主目录

例 2（续）    = = = = − n k P X k Y n k 0 ， (随机变量X 与Y的独立性) ( ) = − − − − =  n k k n k e n k e 0 k 1 1 2 2 ! !          = = = = − n k P X k P Y n k 0 ( ) = ( ) − + −  − = n k k n k k n k e 0 1 2 ! ! 1 1 2     ( ) ( ) = − − +  − = n k k n k k n k n n e 0 1 2 ! ! ! ! 1 2     第三章 随机变量及其分布 §5 多维随机变量函数的分布 返回主目录

第三章 随机变量及其分布 例2（续） §5多维随机变量函数的分布 e+a2) n 8 即， p(z=n)=Aem) n (n=0,1,2,.） 由Poisson分布的定义，知Z=X+Y服从参数为 +元，的Poisson分布. 合】返回主目录

例 2（续） ( ) = − − + =   n k k k n k Cn n e 0 1 2 ! 1 2     ( ) ( ) n n e 1 2 ! 1 2     = + − + 即，  ( ) ( ) 1 2 !  1 +  2 −  + = = e n P Z n n (n = 0，1， 2， ) 的 分布． 由 分布的定义，知 服从参数为 Poisson Poisson  1 +  2 Z = X +Y 第三章 随机变量及其分布 §5 多维随机变量函数的分布 返回主目录

第三章 随机变量及其分布 连续型随机变量和的分布 §5多维随机变量函数的分布 设(X,Y)是二维连续型随机变量，其联合密度函 数为f(x,y), 令：Z=X+Y, 下面计算随机变量Z=X+Y的密度函数f(2): 首先计算随机变量Z=X+Y的分布函数F(2): F)=P{Z≤z}=P{X+Y≤z =「fx,yd x+≤2 合返回主目录

连续型随机变量和的分布 ( ) 数为 ( ， )， 设 ， 是二维连续型随机变量，其联合密度函 f x y X Y 令： Z = X +Y， 下面计算随机变量Z = X +Y的密度函数 f Z (z)． 首先计算随机变量Z = X +Y的分布函数FZ (z)． FZ (z) = PZ  z = PX +Y  z ( )  +  = x y z f x， y dxdy 第三章 随机变量及其分布 §5 多维随机变量函数的分布 返回主目录

第三章 随机变量及其分布 连续型随机变量和的分布 §5多维随机变量函数的分布 =j了f, 作变换：y=u-x y 则有 x+y=z F,e)=j了f,u-xa Jduf f(x.u-xyds 合返回主目录

连续型随机变量和的分布 ( )   − − + − = z x dx f x， y dy x y O 作变换：y = u − x 则有( ) ( )   − + − = − z FZ z dx f x， u x du ( )   + − − = du f x u − x dx z ， 第三章 随机变量及其分布 §5 多维随机变量函数的分布 返回主目录

第三章 随机变量及其分布 连续型随机变量和的分布 §5多维随机变量函数的分布 注意里层的积分是u的函数： gu)=∫f(x,u-x 即有 F(=)=[g(u)du 由分布函数与密度函数之间的关系，上式对z求 导，可得Z=X+Y的密度函数为 6-g6-是joa=6 合】返回主目录

连续型随机变量和的分布 注意里层的积分是u的函数： ( ) ( )  − = z 即有 FZ z g u du ( ) ( )  + − g u = f x， u − x dx 导，可得 的密度函数为 由分布函数与密度函数之间的关系，上式对 求 Z X Y z = + f (z) F (z) Z Z =  ( )         =  − z g u du dz d = g(z) 第三章 随机变量及其分布 §5 多维随机变量函数的分布 返回主目录