
第四章 随机变量的数字特征 §1数学期望 §1数学期望 例1:某班有N个人,其中有n个人为a,分,i=1,2,.k, 求平均成绩。 解: 平均成绩为: 2an立贤 若用X表示成绩,则PX=a为 立是立x=a i-1 合】返回主目录
例 1:某班有 N 个人,其中有 i n 个人为 i a 分,i = 1,2,k , n N k i i = =1 , 求平均成绩。 第四章 随机变量的数字特征 §1 数学期望 §1 数学期望 解: 平均成绩为: = = = k i i i k i i i N n a n a N 1 1 1 若用 X表示成绩,则 N n P X a i { = i } = = = k i i i k i i i a P X a N n a 1 1 { } 返回主目录

第四章 随机变量的数字特征 1、数学期望定义 §1数学期望 (1)离散型 设离散型随机变量X的分布律为: P{X=x}=Pk,k=1,2,., 若级数∑xP:绝对收敛, 则称级数∑xP:的和为随机变量X的数学期望。 记为EX,即EX=∑xP& 数学期望也称为均值。 合】返回主目录
1、数学期望定义 设离散型随机变量 X 的分布律为: k pk P{X = x } = ,k = 1,2, , 若级数 i=1 k pk x 绝对收敛, 则称级数 i=1 k pk x 的和为随机变量 X 的数学期望。 记为 EX,即 EX= k=1 k pk x 。 (1) 离散型 第四章 随机变量的数字特征 §1 数学期望 数学期望也称为均值。 返回主目录

第四章 随机变量的数字特征 §1数学期望 (2)、连续型 设连续型随机变量X的概率密度为f(x), 若积分∫xx)dk绝对收敛,则称积分∫x) 的值为X的数学期望。记为EX=x)dk, 数学期望也称为均值。 合】返回主目录
设连续型随机变量 X 的概率密度为 f (x), 若积分 − x f (x)dx绝对收敛,则称积分 − x f (x)dx 的值为 X 的数学期望。记为 EX= − x f (x)dx, 数学期望也称为均值。 (2)、连续型 第四章 随机变量的数字特征 §1 数学期望 返回主目录

第四章 随机变量的数字特征 说明 §1数学期望 ()X的熟桌钼盾]1X企的的厚 取恤关1 叫:ys世理群察2心阳圳甲f额粱∑x 蚕尔阳太阅厚·国耶·丫电泉孤∑6源4 (⑤)甲土闺企雪的素钼羊业的晋谭企雪X 合】返回主目录
第四章 随机变量的数字特征 说 明 §1 数学期望 (1) X的数学期望刻划了X 变化的平均值. 的求和顺序无关. 时,才能保证级数 的和与其级数 变化的平均值,因此,只有当级数 绝对收敛 由于随机变量 的数学期望表示的是随机变量 = = = 1 1 1 (2) n n n n n n n n n x p x p x p X X 返回主目录

第四章 随机变量的数字特征 例2 §1数学期望 由’了¥丫平邶]的斟平火本甲上肇总用: :由平中的议熟: 人:了平中的业 X 8 9 10 P 0.1 0.3 0.6 Y 8 9 10 P 0.2 0.5 0.3 回一火丫的朗平K本s受 合】返回主目录
第四章 随机变量的数字特征 §1 数学期望 甲、乙两人射击,他们的射击水平由下表给出: X:甲击中的环数; Y:乙击中的环数; X 8 9 10 P 0.1 0.3 0.6 Y 8 9 10 P 0.2 0.5 0.3 试问哪一个人的射击水平较高? 例2 返回主目录

第四章 随机变量的数字特征 例2(续) §1数学期望 由了的丛问业2 EX=8×0J+∂×03+J0×0Q=∂2 EX=8×0下+∂×02+J0×03=òJ ☑吓·Y本问业下昌·由的斟里水本垂R了的社 合】返回主目录
第四章 随机变量的数字特征 §1 数学期望 解: 例2(续) 甲、乙的平均环数可写为 EX = 80.1+ 90.3+10 0.6 = 9.5 EY =80.2+90.5+100.3= 9.1 因此,从平均环数上看,甲的射击水平要比乙的好. 返回主目录

第四章 随机变量的数字特征 例3 §1数学期望 夺厘『企雪X胳YC9cY业·首最A尿P “+灯 1T司 (0<<+o) 甲1 =十00 -00 深举诅斗丸()业银4·图业E以业基年 +00 合】返回主目录
第四章 随机变量的数字特征 §1 数学期望 设随机变量X 服从Cauchy分布,其密度函数为 由于 ( ) + − x f x dx ( ) (− +) + = x x f x 2 1 1 1 + − + = dx x x 2 1 1 + + = 0 2 1 2 dx x x ( ) + = + 0 2 ln 1 1 x = + 这表明积分 ( ) 不绝对收敛, + − xf x d x 因而EX 不存在. 例3 返回主目录

第四章 随机变量的数字特征 §1数学期望 例4 设离散型随机变量X的分布律为: 1 2 P0.1 0.20.7 则 EX=0*0.1+1*0.2+2*0.7=1.6 若离散型随机变量X的分布律为: X012 P0.70.20.1 则 EX=0*0.7+1*0.2+2*0.1=0.4 此例说明了数学期望更完整地刻化了x的均值状态。 合]返回主目录
设离散型随机变量 X 的分布律为: X 0 1 2 P 0.1 0.2 0.7 例 4 则 EX = 0*0.1+1*0.2+2*0.7 =1.6 若离散型随机变量 X 的分布律为: X 0 1 2 P 0.7 0.2 0.1 则 EX = 0*0.7+1*0.2+2*0.1 =0.4 第四章 随机变量的数字特征 §1 数学期望 此例说明了数学期望更完整地刻化了x的均值状态。 返回主目录
第四章 随机变量的数字特征 例5 按规定,火车站每天800~900,9001000都恰 有一辆客车到站,但到站的时刻是随机的,且两 者到站的时间相互独立,其规律为: 到站时间8:10,9:10 830,930 8:50.9:50 概率 1/6 3/6 2/6 (1)旅客8:00到站,求他侯车时间的数学期望。 (2)旅客820到站,求他侯车时间的数学期望。 解:设旅客的候车时间为X(以分记) (1)X的分布律:X103050 P1/63/62/6 EX=10*(1/6)+30*(376)+50*(2/6)=33.33(分) 合】返回主目录
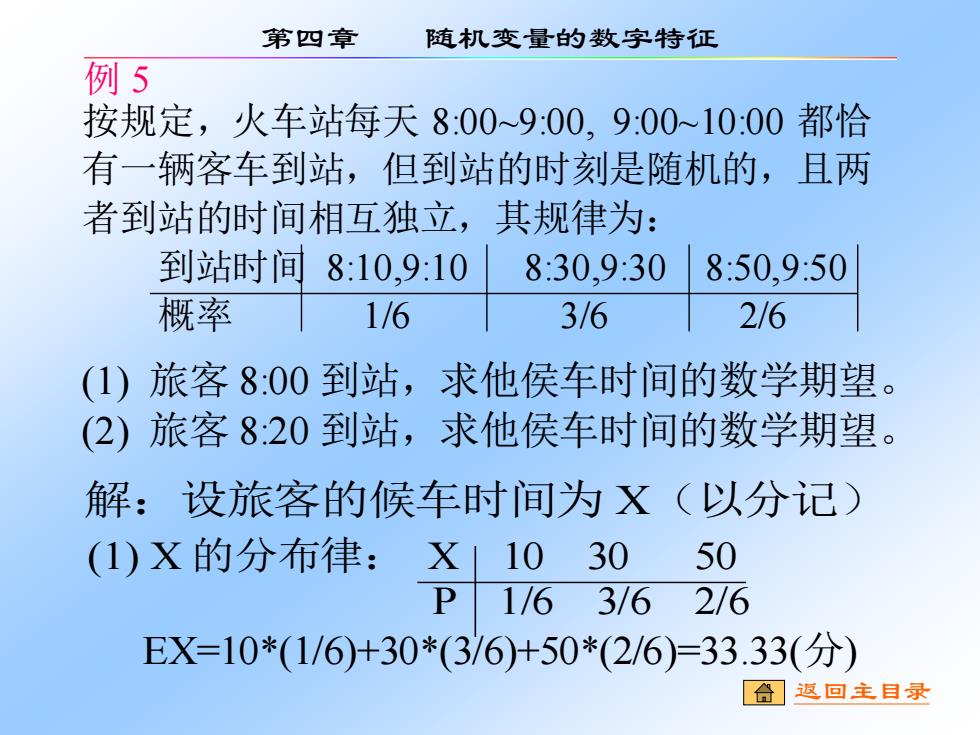
按规定,火车站每天 8:00~9:00, 9:00~10:00 都恰 有一辆客车到站,但到站的时刻是随机的,且两 者到站的时间相互独立,其规律为: 到站时间 8:10,9:10 8:30,9:30 8:50,9:50 概率 1/6 3/6 2/6 例 5 解:设旅客的候车时间为 X(以分记) (1) X 的分布律: X 10 30 50 P 1/6 3/6 2/6 EX=10*(1/6)+30*(3/6)+50*(2/6)=33.33(分) 第四章 随机变量的数字特征 (1) 旅客 8:00 到站,求他侯车时间的数学期望。 (2) 旅客 8:20 到站,求他侯车时间的数学期望。 返回主目录

第四章 随机变量的数字特征 §1数学期望 (2)旅客8.20分到达 X的分布率为 X103050 70 90 P3/62/6(1/6)*(1/6)(3/6)*(1/6)(2/6)*(1/6) EX=10*(3/6)+30*(2/6)+50*(1/36)+70*(3/36)+90*(2/36) =27.22(分) 到站时间 8:10.910 830.930 850.9:50 概率 1/6 316 216 合 返回主目录
X 10 30 50 70 90 P 3/6 2/6 (1/6)*(1/6) (3/6)*(1/6) (2/6)*(1/6) EX=10*(3/6)+30*(2/6)+50*(1/36) +70*(3/36) +90*(2/36) =27.22(分) 第四章 随机变量的数字特征 §1 数学期望 到站时间 8:10,9:10 8:30,9:30 8:50,9:50 概率 1/6 3/6 2/6 (2)旅客8:20分到达 X的分布率为 返回主目录