
§3.6随机变量的独立性 事件A与B独立的定义是: 若PAB)=P(A)P(B),则称事件A与B相互 独立。 设X,Y是两个随即变量,对任意的x,y,若 PX≤x,Y≤y)=P(X≤x)P(Y≤y) 则称X与Y相互独立。用联合分布函数与边缘 分布函数表示上式,就是 F(x,y)=Fx(x)Fy(y)
§3.6 随机变量的独立性 事件A与 B独立的定义是: 若 P(AB) = P(A)P(B),则称事件A与B相互 独立 。 设 X, Y是两个随即变量, 对任意的x, y, 若 P(X x, Y y) = P(X x) P(Y y), 则称 X与Y 相互独立。用联合分布函数与边缘 分布函数表示上式, 就是 F(x, y) F (x) F (y). = X Y

若X,)是连续型随机向量,上述独立性 定义等价于:对任意x,y∈R,有 f(x,y)=f(x)f (y) 几乎总成立,则称X与相互独立 其中f(x,y)是X,)的联合密度,fx(x)与f(y) 分别是的边缘密度和Y的边缘密度。 这里“几乎总成立”的含义是:在平面上 除去一个面积为零的集合外,公式成立
其中 f (x, y) 是(X,Y)的联合密度, 若 (X,Y) 是连续型随机向量,上述独立性 定义等价于:对任意x, y∈ R, 有 这里“几乎总成立”的含义是:在平面上 除去一个面积为零的集合外,公式成立。 f (x) f (y) X 与 Y 分别是X的边缘密度和Y 的边缘密度。 f (x, y) f (x) f (y) = X Y 几乎总成立, 则称X与Y相互独立

若X,)是离散型随机变量,则上述独立性 定义等价于:对X,)所有可能取值化,),有 P(X=xY=y)=P(X=x)P(Y=Y) 成立,则称X与Y相互独立。 @@的
若 (X,Y)是离散型随机变量,则上述独立性 定义等价于:对(X,Y) 所有可能取值 (xi , yj ), 有 ( , ) ( ) ( ) i j i j P X =x Y = y = P X =x P Y = y 成立,则称 X与Y 相互独立
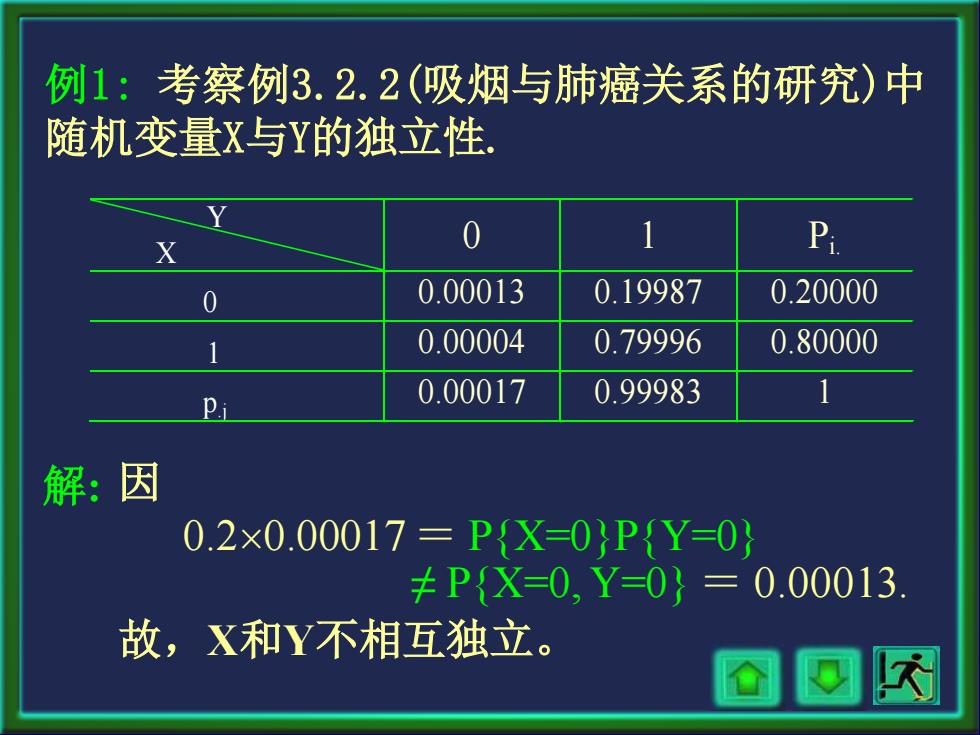
例1:考察例3.2.2(吸烟与肺癌关系的研究)中 随机变量X与Y的独立性 0 P 0 0.00013 0.19987 0.20000 0.00004 0.79996 0.80000 0.00017 0.99983 1 解:因 0.2×0.00017=PX=0}PY=0 ≠PX=0,Y=0}=0.00013 故,X和Y不相互独立
解: 例1: 考察例3.2.2(吸烟与肺癌关系的研究)中 随机变量X与Y的独立性. Y X 0 1 Pi. 0 0.00013 0.19987 0.20000 1 0.00004 0.79996 0.80000 p.j 0.00017 0.99983 1 因 0.20.00017 = P{X=0}P{Y=0} ≠ P{X=0, Y=0} = 0.00013. 故,X和Y不相互独立

例2:设(X,)~N(1,山2,1,o2,p),求证: X与Y独立的充要条件为p=0。 证明:因 fx,)= 1-02) 0101 2π2V1- fx()=2πo 2o2 (y-42)2 f,(y)=2元o2 @四的
证明:因 例2:设(X,Y)∼N(1,2,1,2,), 求证: X与Y 独立的充要条件为 = 0。 , 2 1 1 ( , ) 2 2 2 2 1 2 1 2 2 1 2 1 2 ( )( ) ( ) 2 ( ) 2(1 ) 1 2 1 2 − + − − − − − − − = x u x u y u y u f x y e , 2 1 ( ) 2 1 2 1 1 2 ( ) 1 − − = x f X x e . 2 1 ( ) 2 2 2 2 2 ( ) 2 − − = y f Y y e

“=”将p=0代入联合概率密度函数,得 fx,)= 2π002 (x-4)2 1 (y-42)2 2o1 2o3 J2π01 √2π02 =fx(x)fy(). 所以,X与Y相互独立。 @@函
“” 将=0代入联合概率密度函数,得 − + − − = 2 2 2 2 2 1 2 1 ( ) ( ) 2 1 1 2 2 1 ( , ) x u y u f x y e ( ) ( ). 2 1 2 1 2 2 2 2 2 1 2 1 2 ( ) 2 2 ( ) 1 f x f y e e X Y x u y u = = − − − − 所以,X与Y相互独立

→”若X和Y相互独立,则V(x,)∈R2,有 f(x,y)=fx (x)fy (p). 特别地,将x=4,y=42代入上式,有 f012)=f41f2), 即 2πoo2V1-p2 √J2元01√2π02 从而,p=0。 @回风
“” 若X和Y相互独立,则 (x, y)R 2,有 f (x, y)=f X(x) f Y(y). 从而, = 0。 . 2 1 2 1 2 1 1 1 2 2 1 2 = − 特别地,将 x =μ1, y =μ 2 代入上式,有 f (μ1 ,μ2 ) = fX(μ1 )fY(μ2 ), 即

例3:设X,)的概率密度为 /n= xe-(x+r) x>0,y>0, 0, 其他 问:X与Y是否独立? 解:fx(x)=xe(xdy=xe,x>0, fy(y)=[xed =e,y>0. 从而,对一切x,y∈R,均有 f(化,y)fxc)fv): 故,X与Y是否相互独立
解: − + = 0 ( ) f (x) xe dy x y X − + = 0 ( ) f ( y) xe dx x y Y = , 0, − xe x x = , 0. − e y y 从而,对一切 x, y∈R , 均有 f (x, y)=f X(x) f Y(y). 故,X与Y是否相互独立。 例3: 设(X,Y) 的概率密度为 = − + 0, . , 0, 0, ( , ) ( ) 其他 xe x y f x y x y 问:X与Y是否独立?

例4:若CX,)的概率密度为 2,0<x<y,0<y<1, f(x,y)= o其他 问X与Y是否独立? 解:f(x)=2d=21-x,0<x<1, f(y)=2k=2y,0<y<1. 由于存在面积不为零的区域D,使得 f(x,y)≠fx(x)f(y),(x,y)∈D 故,X与不相互独立
解: ( ) 2 2(1 ), 0 1, 1 = = − f x dy x x x X ( ) 2 2 , 0 1. 0 = = f y dx y y y Y 由于存在面积不为零的区域 D,使得 f (x, y) f (x) f (y), (x, y) D. X Y 故,X与Y不相互独立 。 例4:若(X,Y)的概率密度为 = 0, . 2, 0 , 0 1, ( , ) 其他 x y y f x y 问X与Y是否独立?

§3.7 随机变量函数的分布 3.7.1离散型分布情形 例1:若X与Y独立,且PX=)=4k,k=0,1,2,., P(Y=k)=b.,=0,1,2,求Z=X+Y的概率分布。 解:P(Z=)=P(X+Y=r) = ∑P(X=i,Y=r-) ∑PX=0PCY=r-) i= =ab,+ab,1+.+a,-b+a,b, r=0,1,2,. @四风
3.7.1 离散型分布情形 例1:若X与Y独立,且P(X=k)=ak , k=0,1,2, . , P(Y=k)=bk , k=0,1,2, ., 求 Z=X+Y 的概率分布。 解: P(Z = r) = P(X +Y = r) = = = = − r i P X i P Y r i 0 ( ) ( ) = = = = − r i P X i Y r i 0 ( , ) §3.7 随机变量函数的分布 , = a0 br + a1 br−1 ++ ar−1 b1 + ar b0 r = 0,1,2,