
§4.2方差 前面介绍了随机变量的数学期望。数 学体现了随机变量取值的平均水平,是随 机变量的重要的数字特征。 但在一些场合,仅仅知道平均值是不够 的,还需了解其他数字特征
前面介绍了随机变量的数学期望。数 学体现了随机变量取值的平均水平,是随 机变量的重要的数字特征。 但在一些场合,仅仅知道平均值是不够 的,还需了解其他数字特征。 §4.2 方差
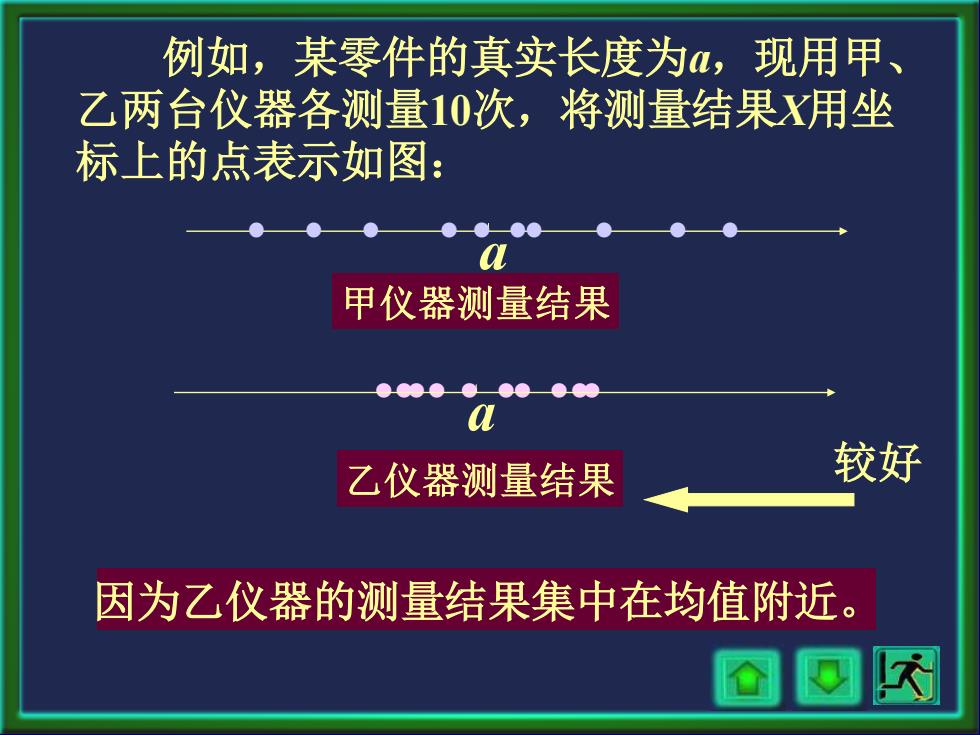
例如,某零件的真实长度为α,现用甲、 乙两台仪器各测量10次,将测量结果X用坐 标上的点表示如图: 甲仪器测量结果 乙仪器测量结果 较好 因为乙仪器的测量结果集中在均值附近
例如,某零件的真实长度为a,现用甲、 乙两台仪器各测量10次,将测量结果X用坐 标上的点表示如图: a •••• • •• ••• 乙仪器测量结果 a • • • • • •• • • • 甲仪器测量结果 较好 因为乙仪器的测量结果集中在均值附近
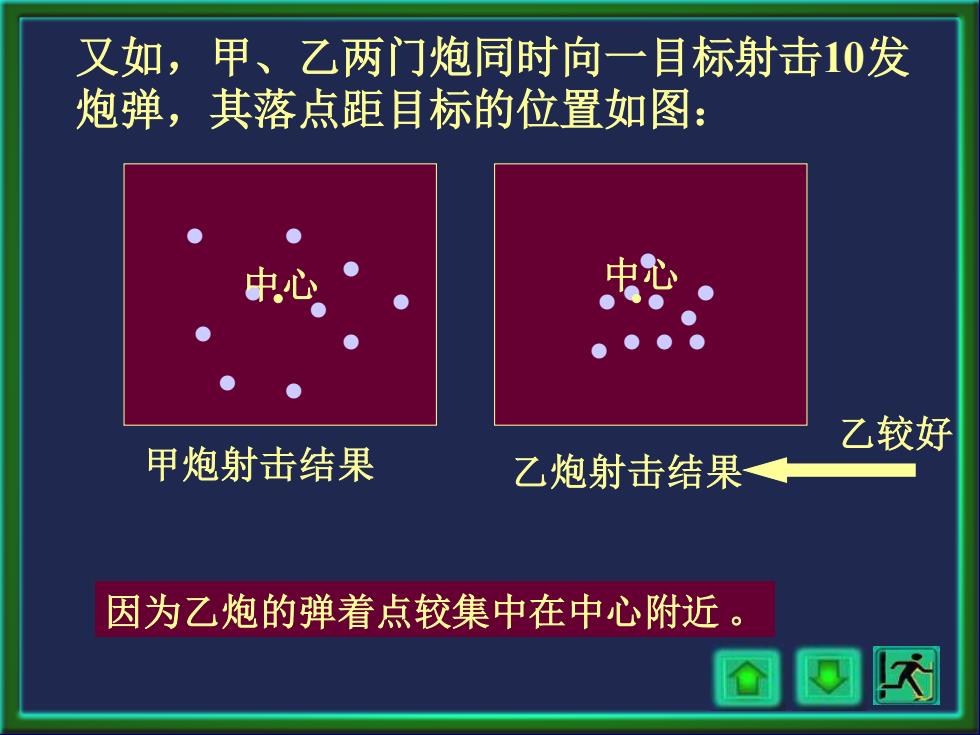
又如,甲、乙两门炮同时向一目标射击10发 炮弹,其落点距目标的位置如图: 乙较好 甲炮射击结果 乙炮射击结果 因为乙炮的弹着点较集中在中心附近
又如,甲、乙两门炮同时向一目标射击10发 炮弹,其落点距目标的位置如图: 甲炮射击结果 乙炮射击结果 乙较好 因为乙炮的弹着点较集中在中心附近 。 • • • • • • • • • • • • • • • • • • • • 中心 中心

为此需要引进另一个数字特征,用它来 度量随机变量取值偏离其中心(均值)的程度。 这个数字特征就是我们要介绍的方差
为此需要引进另一个数字特征,用它来 度量随机变量取值偏离其中心(均值)的程度。 这个数字特征就是我们要介绍的方差

4.2.1方差的定义 采用平方是为了保证一切 差值X-EX)都起正的作用 定义1:设X是一随机变量,若EX-EX)P 存在,则称其为X的方差,记成Var),即 Var(X)=E[X-E(X)2; 并称Wa(X)为X的标准差。 注:有的书上也将Var记成D)
4.2.1 方差的定义 注: 有的书上也将Var(X)记成D(X)。 定义1: 设X 是一随机变量,若E[X-E(X)]2 存在, 则称其为X 的方差,记成Var(X),即 Var(X)= E[X-E(X)]2 ; (1) 并称 Var(X) 为X的标准差。 采用平方是为了保证一切 差值[X-E(X)]都起正的作用

方差刻划了随机变量的取值对于其数学 期望的偏离程度。 若X的取值比较集中,则方差较小; 若X的取值比较分散,则方差较大。 若方差arX=0,则X以概率1取常数。 均值E)
若X 的取值比较分散,则方差较大。 若方差Var(X)=0,则 X 以概率1取常数。 方差刻划了随机变量的取值对于其数学 期望的偏离程度。 若X 的取值比较集中,则方差较小; 均值E(X)

由定义知,方差是随机变量的函数 g)=X-E)1P的数学期望。 为离散型, P(X-XR)-PK ∑Ix&-E(XP [x-E(X)P'f(x)dx, X为连续型, fc)为密度
X为离散型, P{X=xk }=pk 由定义知,方差是随机变量X的函数 g(X)=[X-E(X)]2的数学期望 。 − − = − = [ ( )] ( ) , [ ( )] , ( ) 2 1 2 x E X f x dx x E X p Var X k k k X为连续型, f (x)为密度

计算方差的一个简化公式 Var(X)=E(X2-E(X)2. 证:arX)=EX-EX凶2 展开 利用期 望性质 =E{X2-2XE凶+[EX]2} =EX)-2IEX12+[E12 =E2)-E]2. @@风
计算方差的一个简化公式 Var(X)=E(X2 )-[E(X)]2 . 证:Var(X)=E[X-E(X)] 展开 2 =E{X2-2X E(X)+[E(X)]2} =E(X2 )-2[E(X)]2+[E(X)]2 =E(X2 )-[E(X)]2 . 利用期 望性质

例1:设X服从几何分布,概率分布为 PX=k=p(1-p)1,k=1,2, 其中0<p<1,求Var)。 解:记-1-p,则 E(X)=∑g=P∑(q) 无穷递缩等比 级数求和公式 =r*y八1 交换求和与 求导次序 @回的
例1:设 X 服从几何分布,概率分布为 P(X=k) = p(1- p) k-1 , k=1, 2, ., 其中 0<p<1, 求 Var(X)。 解: 记 q=1-p,则 = − = 1 1 ( ) k k E X kpq = = 1 ( )' k k p q = = 1 ( )' k k p q )' 1 ( q q p − = , 1 p = 交换求和与 求导次序 无穷递缩等比 级数求和公式

00 E(X)=∑kFpg k=1 =Σkk-I)pg+∑pg =pq∑q)”+E(X)) y+ 2-卫 Tarx=瓦x]-[ExT=2-2 1q p
= − = 1 2 2 1 ( ) k k E X k pq = − = − = − + 1 1 1 1 ( 1) k k k k k k p q kpq ( ) ( ) 1 p q q E X k k = + = q p q pq 1 ) 1 ( + − = , 2 2 p − p = . 2 1 ( ) [ ] [ ( )] 2 2 2 2 2 p q p p p Var X E X E X − = − = − =