
§2.2 离散型随机变量 设X是一个离散型随机变量,其可能取 值为X1,X2,.。 为描述随机变量X,我们不仅要知道其 所有可能的取值,还应知道取各值的概率
设X是一个离散型随机变量,其可能取 值为 x1 , x2 , . 。 为描述随机变量 X ,我们不仅要知道其 所有可能的取值,还应知道取各值的概率。 §2.2 离散型随机变量

例1:从盒中任取3球,记X为取 到白球数。则X是一随机变量。 X可能取的值为:0,1,2。取各值的概率为 P(X=0)片 Px 1 :_6 1 C 10 P(X-2)-9C 3 10 且 PX=k)=I· k三0 这样,我们就掌握了X这个取值的概率分布
这样,我们就掌握了X 这个取值的概率分布。 例1:从盒中任取3 球, 记 X 为取 到白球数。则 X 是一随机变量。 X 可能取的值为: 0, 1, 2。取各值的概率为 , 10 1 ( 0) 3 5 3 3 = = = C C P X , 10 6 ( 1) 3 5 1 2 2 3 = = = C C C P X , 10 3 ( 2) 3 5 2 2 1 3 = = = C C C P X 且 ( ) 1。 2 0 = = = k P X k

2.2.1离散型随机变量概率分布的定义 定义1:设离散型随机变量X所有可能取 的值为X1,x2,且有 PX=x=p,k=1,2,.。 则称p,P2,.为离散型随机变量X的概率分布 或分布律,也称概率函数。其中p1,P,.满足 (1).2≥0,k=1,2,. 用这两条性质判断 (2).∑P1 一个数列是否是概 率分布
用这两条性质判断 一个数列是否是概 率分布。 2.2.1 离散型随机变量概率分布的定义 定义1 :设离散型随机变量X 所有可能取 的值为 x1 , x2 , , 且有 P(X=xk )=pk , k =1,2, 。 则称p1 , p2 , .为离散型随机变量X 的概率分布 或分布律,也称概率函数。其中 p1 , p2 , .满足 (1). p 0, k =1,2, ; k (2). =1. k pk

概率分布也可用下面表格的形式给出: X X2 Pk P1 P2 @@的
概率分布也可用下面表格的形式给出:

例2:设随机变量X的概率分布为 2 P(X=k)=a k=0,1,2,.,2>0为常数。 确定常数a。 解: 依据概率分布的性质 P(X=k)≥0, 2PX=)=1 欲使上述数列为概率分布,应有
解:依据概率分布的性质 欲使上述数列为概率分布,应有 例2:设随机变量X 的概率分布为 , 0,1, 2, , 0为常数。 ! ( = ) = = k k P X k a k 确定常数 a 。 ( ) 1. ( ) 0 , = = = k P X k P X k

a≥0与 _=ae"=1 1k=0 从中解得a=e2 这里用到了幂级数展开式 @四的
. − 从中解得 a = e 1. 0 ! = = = ae k a k k a 0 与 这里用到了幂级数展开式 . 0 ! e k k k = =

例3:某篮球运动员投中篮圈概率是0.9,求其 两次独立投篮后,投中次数X的概率分布。 解:X可取的值为:0,1,2,且 PX=0)=(0.1)0.1)=0.01, PX=1)=2(0.9)0.1)=0.18, P=2)=(0.9)0.9)=0.81. 易见:PX=0)+PX=1)+PX=2)=1. @@网
例3:某篮球运动员投中篮圈概率是0.9,求其 两次独立投篮后,投中次数 X 的概率分布。 解:X 可取的值为 :0, 1, 2,且 P(X=0) = (0.1)(0.1) = 0.01, P(X=1) = 2(0.9)(0.1) = 0.18 , P(X=2) = (0.9)(0.9) = 0.81 . 易见: P(X=0) + P(X=1) + P(X=2) = 1
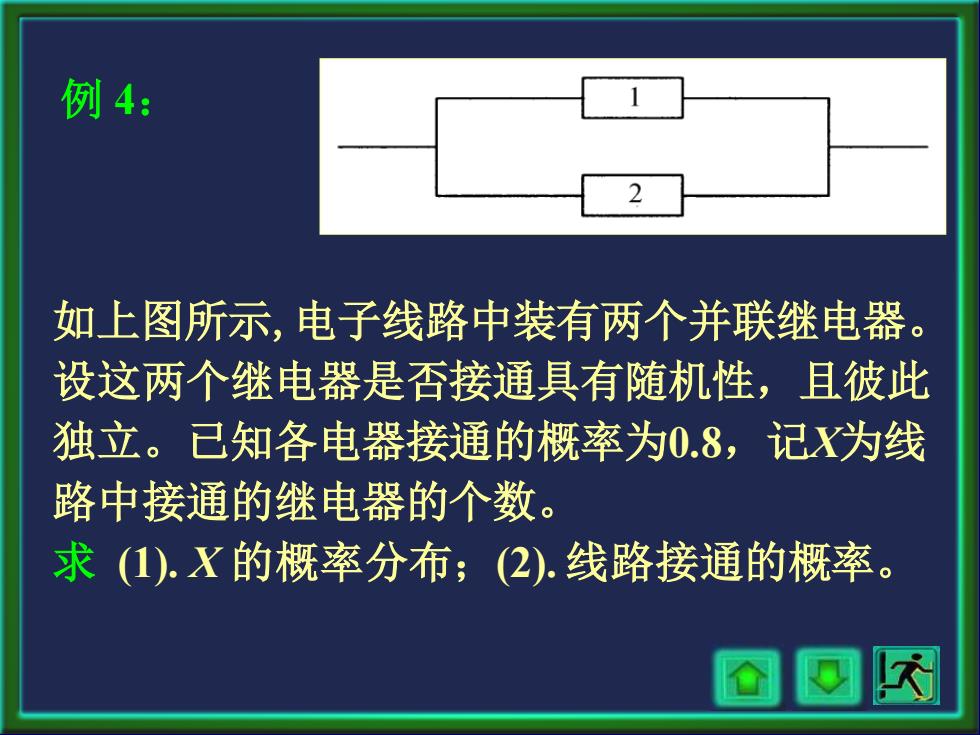
例4: 如上图所示,电子线路中装有两个并联继电器。 设这两个继电器是否接通具有随机性,且彼此 独立。已知各电器接通的概率为0.8,记X为线 路中接通的继电器的个数。 求(1).X的概率分布;(2).线路接通的概率
例 4: 如上图所示,电子线路中装有两个并联继电器。 设这两个继电器是否接通具有随机性,且彼此 独立。已知各电器接通的概率为0.8,记X为线 路中接通的继电器的个数。 求 (1). X 的概率分布;(2). 线路接通的概率
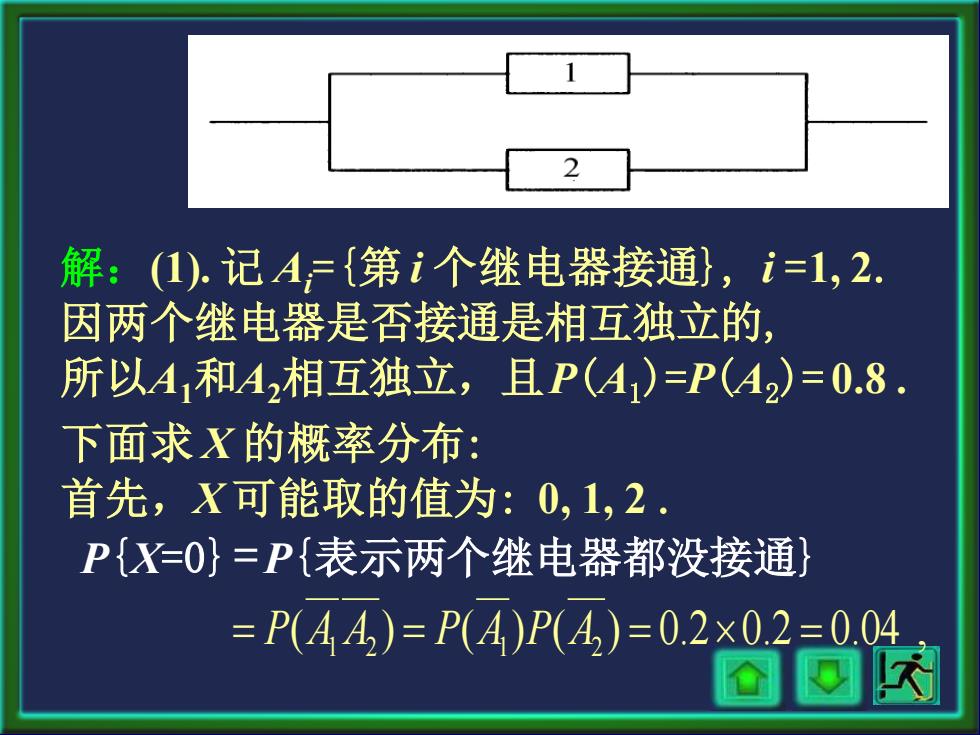
2 解:(1).记A={第i个继电器接通},i=1,2. 因两个继电器是否接通是相互独立的, 所以A和A相互独立,且P(A1)=P(4)=0.8. 下面求X的概率分布: 首先,X可能取的值为:0,1,2. P{X=0}=P{表示两个继电器都没接通} =P(A4)=P(A)P4)=0.2x0.2=0.04
解:(1). 记 Ai={第 i 个继电器接通}, i =1, 2. 因两个继电器是否接通是相互独立的, 所以A1和A2相互独立,且P(A1)=P(A2)= 0.8 . 下面求 X 的概率分布: 首先,X 可能取的值为: 0, 1, 2 . P{X=0} =P{表示两个继电器都没接通} ( ) ( ) ( ) 0.2 0.2 0.04 , = P A1 A2 = P A1 P A2 = =

P{X=1}=P{恰有一个继电器接通} =P(A4)+P(AA) =P(A)P(A)+P(A)P(A) =0.8×0.2+0.2×0.8=0.32 P{X=2}=P{两个继电器都接通} =P(A4) =P(A)P(A) =0.8×0.8 =0.64. @@的
0.8 0.2 0.2 0.8 0.32 , ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 2 1 2 1 2 = + = = + = + P A P A P A P A P A A P A A P{X=1}=P{恰有一个继电器接通} 0.64 . 0.8 0.8 ( ) ( ) ( ) 1 2 1 2 = = = = P A P A P A A P{X=2}= P{两个继电器都接通}