
§1.2事件的概率 1.2.1事件的频率 L.频率定义 设A是一个事件,在相同条件下进行n次试 验,A发生了m次。则称m为事件A在n次试验 中发生的频数或频次,称m与n之比n为事 件A在n次试验中发生的频率,记为f(4)
§1.2 事件的概率 1.2.1 事件的频率 I. 频率定义 设A是一个事件, 在相同条件下进行n次试 验,A发生了m次。则称m为事件A在n次试验 中发生的频数或频次,称m与n之比 m/n 为事 件A在n次试验中发生的频率,记为fn (A)

当试验次数n充分大时,事件的频率总在 一个定值附近摆动,而且,试验次数越多, 一 般说来摆动的幅度越小。这一性质称频率 的稳定性。 频率在一定程度上反映了事件在一次试 验中发生的可能性大小。尽管每进行一连n次 试验,所得到的频率可能各不相同,但只要n 足当大,频率就会非常接近一个固定值 概率。 因此,概率可以通过频率来“度量”,频率 是概率的近似,概率是频率某种意义下的极限
当试验次数 n充分大时,事件的频率总在 一个定值附近摆动,而且,试验次数越多, 一般说来摆动的幅度越小。这一性质称频率 的稳定性。 频率在一定程度上反映了事件在一次试 验中发生的可能性大小。尽管每进行一连 n次 试验,所得到的频率可能各不相同,但只要 n 足当大,频率就会非常接近一个固定值—— 概率。 因此, 概率可以通过频率来“度量” , 频率 是概率的近似, 概率是频率某种意义下的极限
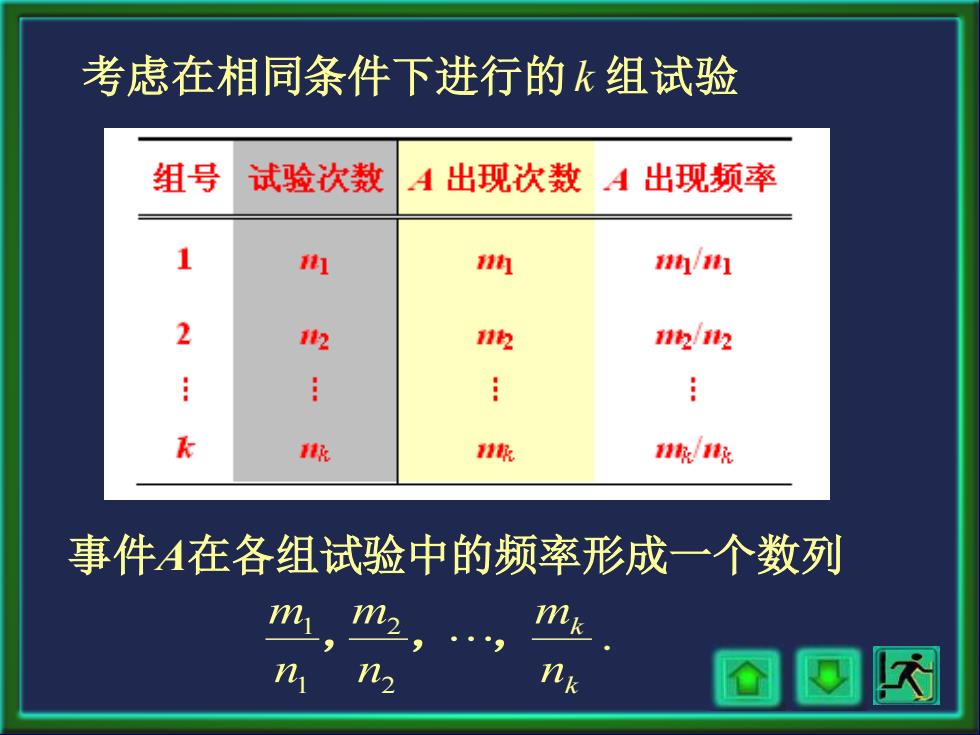
考虑在相同条件下进行的k组试验 组号 试验次数 A出现次数A出现频率 钩 /1 2 2 112 12/12 级 11k 1/11k 事件A在各组试验中的频率形成一个数列 m m n n2
考虑在相同条件下进行的k 组试验 事件A在各组试验中的频率形成一个数列 . 2 2 1 1 k k n m n m n m , ,
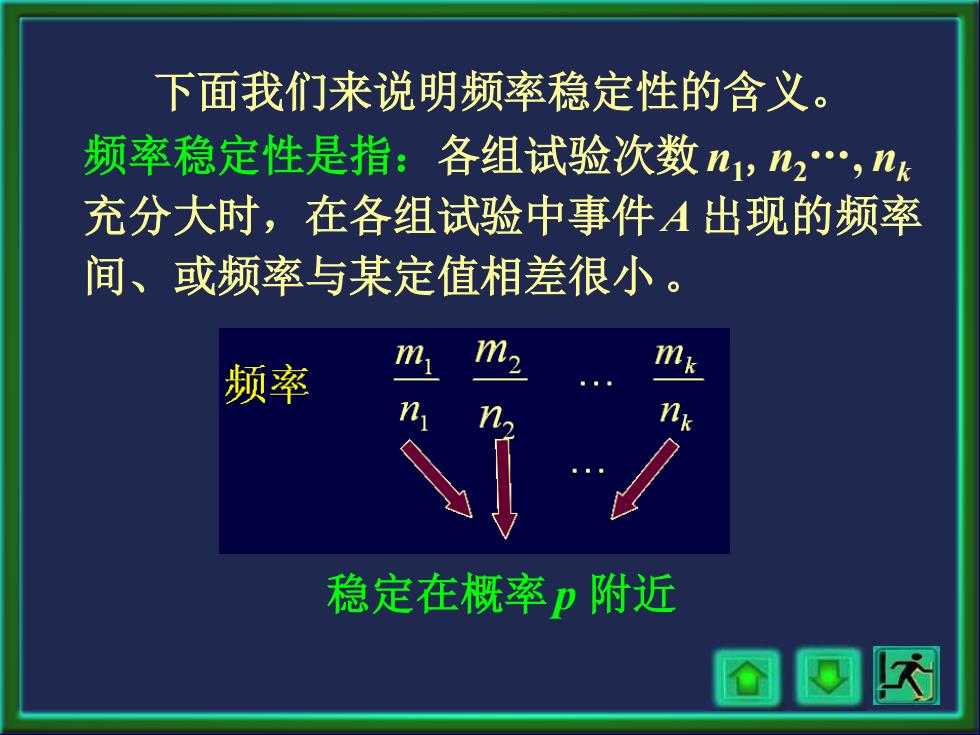
下面我们来说明频率稳定性的含义。 频率稳定性是指:各组试验次数n1,n2.,nk 充分大时,在各组试验中事件A出现的频率 间、或频率与某定值相差很小。 m 频率 稳定在概率p附近 @@
频率稳定性是指:各组试验次数n1,n2 . , nk 充分大时,在各组试验中事件A 出现的频率 间、或频率与某定值相差很小 。 稳定在概率p 附近 下面我们来说明频率稳定性的含义

在实际问题中,当概率不易求出时,人 们在试验次数很大情况下,常用事件的频率 作为概率的估计,并称此概率为统计概率。 这种确定概率的方法为频率法。 例如:若需了解某射箭运动员中10环的概率, 应对该运动员在相同条件下的多次射箭情况 进行观测、统计。 假设其射击n次,中10环m次,当n很大 时,就m/n作为其命中10环的概率
在实际问题中,当概率不易求出时,人 们在试验次数很大情况下,常用事件的频率 作为概率的估计,并称此概率为统计概率。 这种确定概率的方法为频率法。 例如: 若需了解某射箭运动员中10环的概率, 应对该运动员在相同条件下的多次射箭情况 进行观测、统计。 假设其射击n次,中10环m次,当n很大 时,就 m/n 作为其命中10环的概率

又如:进行产品检验时,如果检验了n件产品, 其中m件为次品,则当n很大时,可用mln作 为产品的次品率(概率)的估计值。 @@风
又如:进行产品检验时,如果检验了n 件产品, 其中m 件为次品,则当n 很大时,可用m/n 作 为产品的次品率(概率)的估计值

1.频率性质 (1).0≤f(A)≤1; (2).fn(2)=1,f(0)=0; (3).若事件A1,A2,.,Ak两两互斥,则: .g-名4 @四的
(1) 0≤ fn(A)≤1; (2) fn(Ω)=1, fn(Ø)=0; (3).若事件 A1,A2, . ,Ak 两两互斥,则: II. 频率性质 。 = = = k i n i k i f n Ai f A 1 1 ( )

1.2.2事件概率 L.概率定义 柯尔莫哥洛夫,AH 1933年,前苏联数学家(概率统计学家)柯 尔莫哥洛夫(Kolmogorov)给出了概率如下公理 化定义
1933年,前苏联数学家(概率统计学家)柯 尔莫哥洛夫 (Kolmogorov) 给出了概率如下公理 化定义。 1.2.2 事件概率 I. 概率定义

概率的公理化定义 设E是随机试验,2是样本空间,对2中 的每个事件A,赋予一个实数P(4),如果事 件(集合)函数P(4A)满足下述三条: (1).PA≥0; 2).P(2)=1; (3).若事件A,A2.两两互斥,则有 P(AUAU)=P(A)+P(A)+. 则称P(A)为事件A的概率
概率的公理化定义 (2). P(Ω)=1 ; (3). 若事件A1 , A2 ,. 两两互斥,则有 设E是随机试验,Ω是样本空间,对Ω中 的每个事件A,赋予一个实数P(A) ,如果事 件(集合)函数P(A) 满足下述三条: (1). P(A)≥0; 则称P(A)为事件A的概率。 ( ) ( ) ( ) . P A1 A2 = P A1 + P A2 +

注意:这里的函数P(4)与以前所学过的函 数不同。不同之处在于:P(4)的自变量是事件 (集合)。 不难看出:这里事件概率的定义是在频率 性质的基础之上提出的。在§5.1中,我们将看 到:频率f(4)在某种意义下收敛到概率P(4)的 结论。基于这一点,我们有理由用上述定义的 概率P(A)来度量事件A在一次试验中发生的可 能性大小
注意:这里的函数P(A)与以前所学过的函 数不同。不同之处在于:P(A)的自变量是事件 ( 集合 )。 不难看出:这里事件概率的定义是在频率 性质的基础之上提出的。在§5.1中, 我们将看 到:频率fn (A)在某种意义下收敛到概率P(A)的 结论。基于这一点,我们有理由用上述定义的 概率 P(A)来度量事件A在一次试验中发生的可 能性大小