
§1微分方程及其解的定义 第一章 F(K,y,y0)=0 1.D 应该掌握的基本内容 0 理解微分方程的基本概念:微分方程的定义,微分方程的解,通解特解,初 始条件,线性与非线性方程等概念 1包含自变量,未知函数以及未知函数的某些导数(或微分)的等式称微分方程。 2微分方程中,必定含未知函数的导数的项,其中出现的未知函数导数 的最高阶数就称为该微分方程的阶数 3一般的阶F(x,y,y,ym)=0的初始条件为 ()=o,y(xo)=y1,.y(m-1(xo)=yn-1 1.7) 4若方程(1.1)中的左端为y及,"罗 d. 的一次有理整式,我们就称它为 dxm 阶线性方程式,它的一般形式可写成: a(x)y(+a(x)y(1+.+a(x)y=f(x) (1.6) ○根据实际尚题建立微分方程模型.伉何尚题及物理问顺) 结束 帮助 上一顶返回
结束 帮助 上一页 返回 下一页 目录 首页 应该掌握的基本内容 理解微分方程的基本概念:微分方程的定义,微分方程的解,通解特解,初 始条件,线性与非线性方程等概念. 根据实际问题建立微分方程模型.(几何问题及物理问题) §1 微分方程及其解的定义 1 包含自变量,未知函数以及未知函数的某些导数(或微分)的等式称微分方程。 2 微分方程中,必定含未知函数的导数的项,其中出现的未知函数导数 的最高阶数就称为该微分方程的阶数 = ' ( ) 3 一般的n F x y y y 阶 ( , , ,., ) 0 n 的初始条件为 − = = = − ( 1) 0 0 0 1 0 1 ( ) , '( ) , ( ) (1.7) n y x y y x y y x yn ' ( ) ( , , ,., ) 0 1.1 n F x y y y = ( ) (1.1) ,. n n dy d y y dx dx n 4 若方程 中的左端为 及 的一 次有理整式,我们就称它为 阶线性方程式,它的一般形式可写成: ( ) ( 1) 0 1 ( ) ( ) . ( ) ( ) (1.6) n n n a x y a x y a x y f x − + + + = 第一章

§1微分方程及其解的定义 第二章 要掌握的基本内容:一阶常微分方程的解法 一般的一阶常微分方程式为 F(x,y,y)=0 (1.3) 或 M(x,y)dx+N(x,y)dy=0 (1.4) 或 =f(x,) (1.5) dx 结束 籍助2上一贡扳回下一页<2目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 ( , ) (1.5) dy f x y dx = 或 M x y dx N x y dy ( , ) ( , ) 0 (1.4) + = 或 ' F x y y ( , , ) 0 (1.3) = 一般的一阶常微分方程式为 §1 微分方程及其解的定义 第二章 要掌握的基本内容:一阶常微分方程的解法

复习 1.变量分离方程 d =f(x):g() 可化为变量分离方程的方程 ①齐次方程么=8中,解法:令y=w,则y=+w代入方程,方程化为变量分离方程 2.方程 dy ax+by+c, 解法: dx a2x+b2y+c2 ()C1=c2=0时方程为齐次方程 (im=么时,令=么=k,作变换a,x+D,y=,方程 2 a,b 可化为齐次方程 4x+by+C1=0 (i)若 2r 不金为零时,解方程组 dxyc:0 得唯一解x=a,y再玲 5=x-4,7=y-b方程可化为齐次方程 结束 帮助 返D
结束 帮助 上一页 返回 下一页 目录 首页 1.变量分离方程 复习 = ( ) ( ) dy f x g y dx 可化为变量分离方程的方程 (1 ( ) , )齐次方程 = = + ,解法:令 则 代入方程,方程化为变量分离方程 dy y g y = xu y u xu dx x 2.方程 + + = + + 1 1 1 2 2 2 dy a x b y c ,解法: dx a x b y c ( ) 0 i c c 1 2 = = 时方程为齐次方程 = = = + = 1 1 1 1 2 2 2 2 2 2 ( ) , , 时,令 作变换 方程 可化为齐次方程 a b a b ii k a x b y u a b a b (iii)若 且 不全为零时,解方程组 1 1 2 2 a b a b 1 2 c ,c + + = + + = 1 1 1 2 2 2 0 0 a x b y c a x b y c 得唯一解 x = a, y = b , 再令 = x - a, = y - b方程可化为齐次方程

复习 3.一阶线性微分方程 =P(x)y+Q(x) dx P(x) 常数变易公式 y= Q(x)e dx+c y 4.Bernoulli方程 =P(x)y+Q(x)y” (2.27) dx 解法:令z=y,则方程化为线性方程 ●●6t。8。5。8.086g5e年年。9。·0年9。g·年0 dz =(1-n)P(x)z+(1-n)2(x) ww.wwwwwwwvwvwwwwwrrr 5.恰当方程 M(x,y)dx+N(x,y)dy =0 aM aN ay ax 解为: [M(x,y)dx+N(x,y)dy =c 还可用凑微分法 结束 助 首页
结束 帮助 上一页 返回 下一页 目录 首页 3. 一阶线性微分方程 复习 = + ( ) ( ) dy P x y x dx Q − = + ( ) ( ) P x dx Pdx 常数变易公式 y e x e dx c Q ( ) ( ) (2.27) dy n P x y Q x y dx = + 4.Bernoulli方程 , 1-n 解法:令z = y 则方程化为线性方程 (1 ) ( ) (1 ) ( ) dz n P x z n Q x dx = − + − 5. 恰当方程 + = = M x y dx N x y dy ( , ) ( , ) 0 M N y x 解为: + = 0 0 0 ( , ) ( , ) x y x y M x y dx N x y dy c 还可用凑微分法
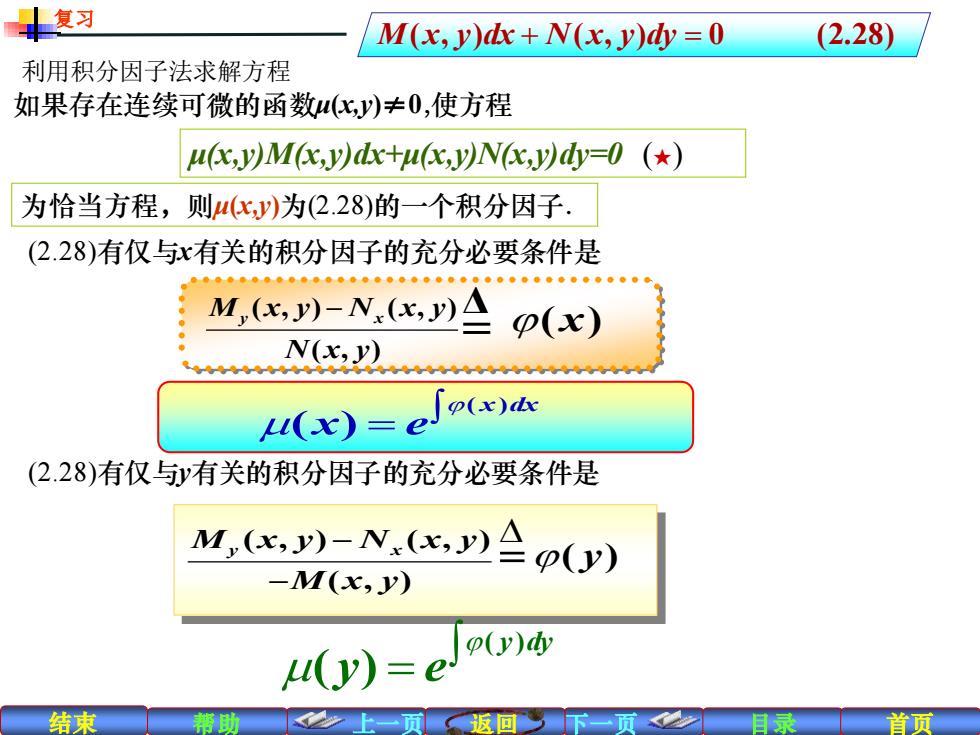
复习 M(x,y)dx+N(x,y)dy =0 (2.28) 利用积分因子法求解方程 如果存在连续可微的函数化y)≠0,使方程 u(x,y)M(,y)dxtu(x,y)N,y)dy=0 ( 为恰当方程,则4(化)为(2.28)的一个积分因子. (2.28)有仅与x有关的积分因子的充分必要条件是 。6●0●0。●●●。●0●。●0●●●。0●。 M(x,y)-N(x,y)△ (x) N(x,y) L(x)=e p(x)d (2.28)有仅与有关的积分因子的充分必要条件是 M,(,y)-N.(, e(v) -M(x,y) (y)=e p() 结束 帮助 返回 贝
结束 帮助 上一页 返回 下一页 目录 首页 ( , ) ( , ) ( , ) M x y N x y y x N x y − Δ ( ) x 利用积分因子法求解方程 如果存在连续可微的函数μ(x,y)≠0,使方程 复习 μ(x,y)M(x,y)dx+μ(x,y)N(x,y)dy=0 (★) 为恰当方程,则μ(x,y)为(2.28)的一个积分因子. M x y dx N x y dy ( , ) ( , ) 0 (2.28) + = (2.28)有仅与x有关的积分因子的充分必要条件是 (2.28)有仅与y有关的积分因子的充分必要条件是 ( , ) ( , ) ( , ) M x y N x y y x M x y − − ( ) y ( ) ( ) y dy y e = = ( ) ( ) x dx x e

复习 阶隐式方程F,y)=0的四种特殊类型方程的求解, 1.可对y解出的方程y=Fcy). 2.可对x解出的方程x=Fy). 3.方程不显含y的方程c,y=0. 4.方程不显含x的方程Fyy)=0. 1.可对y解出的方程y=Fc, 引进参数y=p(x),于是有y=F(x,陋边对x求导,得 OF D l OF ap 结束 一面拔下一页2目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 一阶隐式方程 F(x,y,y')=0 的四种特殊类型方程的求解. 复习 1.可对y 解出的方程 y=F(x,y ’). 2.可对x 解出的方程 x=F(y,y ’). 3.方程不显含y 的方程 F(x,y ’)=0. 4.方程不显含x 的方程 F(y,y ’)=0. 1.可对y 解出的方程 y=F(x,y ’). 引进参数 y p x = ( ), 于是有 y F x p = ( , ) ,两边对x求导,得 − = F p dp x dx F p

复习 2.可对x解出的方程x=Fy月. 引进参数y=py) 于是有x=F(y,函边对x求导,得 1 aF dp =P ay dy OF Op 3.方程不显含y的方程Fcy)=0. 令y'=p,F(x,p)=0 x=(t),p=v(t) (t为参数) 而=p'(t)t,所以少=yw(t)w'(t)dt. x=e(t) y=w(t)o'dt+c 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 2.可对x解出的方程 x=F(y,y ’). 复习 引进参数 y p y = ( ), 于是有 x F y p = ( , ) ,两边对x求导,得 − = 1 F dp p y dy F p 3.方程不显含y的方程 F(x,y ’)=0. 令y p F x p = = , ( , ) 0 x t p t t = = ( ), ( ) ( ) 为参数 而 dx t dt = '( ) ,所以 dy t t dt = ( ) '( ) . ( ) ( ) ' x t y t dt c = = +

4.方程不显含x的方程Fyy=0. 对于方程F(y,y)=0.令y'=是 F(y,p)=0 引入参数t,将上式表为适当的参数形式: y=(),D=W(t) dy pdx,(t)dt =v(t)dx x=8→x=∫8m+c w() 于是 dt+C (t 为方程的参数形式的通解 若F(y,0有实根 y 也是解k 结束 上一贡版下一<2 首页
结束 帮助 上一页 返回 下一页 目录 首页 引入参数t ,将上式表为适当的参数形式: y t p t = = ( ) ( ) , dy pdx t dt t dx = = , '( ) ( ) '( ) '( ) ( ) ( ) t t dx dt x dt C t t = = + , 若 F y( , 0) 0 有实根 = ,则 y k = 也是解 y k =. '( ) ( ) ( ) t x dt C t y t = + = 于是 为方程的参数形式的通解 对于方程 F y y ( , ') 0. = 令 y p ' = 于是 F y p ( , ) 0 = 4.方程不显含x的方程 F(y,y ’)=0

复习 练习题: 、指出下列微分方程的阶数,并判断是否为线性方程: 1、 =4x2-y2、 d42+2y +3y=03、 +cosy+x=0 d x dx 4 是+染+9y= dx (1.一阶线性微分方程;2.二阶齐次线性微分方程;3.一阶非线性微分方程4.二阶非线性 微分方程) 二、证明函数y(x)=2ex+xex是方程y"+2y'+y=0的一个解 三、设一曲线有如下的性质:曲线上各点处的切线,切点到原点的向径及x轴可围成一个 等腰三角形(以x轴为底)且通过(1,2),求该曲线的方程满足的微分方程及定解条件 设曲线方程为y=y(x),A(x,y)为曲线上任意一点,则过A的切线方程为 y-y=(X-x dx 所以切线与x轴的交点坐标是(x一 ,0),由题意知4ol=|AB 所以 r+y ①)=2 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 复习 练习题: 一、指出下列微分方程的阶数 2 ,并判断是否为线性方程: 2 2 2 2 1 4 2 2 3 0 3 cos 0 4 ( ) ( ) ( ) dy d y dy dy x y y xy y x dx dx dx dx d y dy p x q x y f x dx dx = − + + = + + = + + = 、 、 、 、 ( ) 2 2 0 x x y x e xe y y y − − 二、证明函数 = + + + = 是方程 的一个解 三、设一曲线有如下的性质:曲线上各点处的切线,切点到原点的向径及x轴可围成一个 等腰三角形(以x轴为底)且通过(1,2),求该曲线的方程满足的微分方程及定解条件 (1. 一阶线性微分方程;2.二阶齐次线性微分方程; 3.一阶非线性微分方程;4.二阶非线性 微分方程) 解 设曲线方程为y y x A x y = ( ), ( , )为曲线上任意一点,则过A的切线方程为 ( ) dy Y y X x dx − = − 1 x x y ( , 0), y − 所以切线与 轴的交点坐标是 由题意知 Ao AB = 所以 2 2 2 2 ( ) (1) 2 x x y y y y + = + =

复习 四、求下列初值问题的解 1、2-y+22=0,0)=12、y-y=F-,0= 解方法1 将方程改写为 2x dx, (1) x2-1 两边积分得 -ink-e 为了确定所求特解,以x=0,y=1代入上式,即可解得c=1.因而所求特解是 1 y= 1+In x2-1 方法2 将(1)两边积分得 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 2 2 2 1 1 1) 2 0, (0) 1; 2 , (1) 2 2 x y xy y xy y x y y − + = = − = − = 四、求下列初值问题的解 、( 、 复习 解 方法1 将方程改写为 2 2 1 2 , (1) 1 x dy dx y x − = − 两边积分得 1 2 ln 1 x c y = − + 为了确定所求特解,以x=0,y=1代入上式,即可解得c=1. 因而所求特解是 2 1 1 ln 1 y x = + − 方法2 将(1)两边积分得 2 2 1 0 1 2 1 y x x dy dx y x − = − 2 1 1 ln 1 y x = + −