新疆大学：《常微分方程》课程教学资源（PPT课件讲稿）第五章 线性微分方程组 §5.3 常系数线性方程组

线性微分方程组 §5.3.常系数线性方程组 5.3.1矩阵指数expA的定义和性质 考虑常系数线性方程组 x =Ax (5.33) 其中是x常数矩阵.为了简明(5.33)的基解矩阵的结果， 首先介绍一下在线性微分方程的研究中一个十分重要的矩阵函 数，即矩阵指数函数 e4 =expA 对任意的X矩阵考虑矩阵函数 会=E+4+ 2! + m! +.(5.34) (这里规定A°=E,0!=是軍位矩牌. (5.34)对于任何A是收敛的.因对一切k>0 k k! 结束 助 目录 首页

结束 帮助 上一页 返回 下一页 目录 首页 §5.3.常系数线性方程组 考虑常系数线性方程组 ' x Ax = （5.33） 其中 是 常数矩阵.为了简明（5.33）的基解矩阵的结果， 首先介绍一下在线性微分方程的研究中一个十分重要的矩阵函 数，即矩阵指数函数. A n n exp A e A = 线性微分方程组 5.3.1矩阵指数expA的定义和性质 对任意的 n n 矩阵 ，考虑矩阵函数 A 2 0 . . ! 2! ! k m k A A A E A k m  =  = + + + + + （5.34） （这里规定 是 单位矩阵 . 0 A E = = ,0! 1) E n n （5.34）对于任何 A 是收敛的.因对一切 k ，  0 ! ! k A k A k k 

事朵数线性微分方程组 ex=1+x+ 而正项数值级数 2! n! 会-+4+4 .=n-1+e4 A 故由矩阵级数收敛的Veierst测法知，级数 k！ 收敛，即(5.34)确定了一个矩阵.我们用x裘际.即称为矩阵指 数函数 定义：函数矩阵指数函数 1-会对 k! pAt=∑4 k! 它在t的任何有限区间内一致收敛的.因为当k>0,时≤c ss k! k! 而 k=0 结束 帮助 返回

结束 帮助 上一页 返回 下一页 目录 首页 而正项数值级数 2 0 . 1 ! 2 k A k A A E A n e k  =  = + + + = − + 故由矩阵级数收敛的 判别法知,级数 收敛,即(5.34)确定了一个矩阵.我们用 表示.即称为矩阵指 数函数 Weierstrass 0 ! k k A k  =  exp A 0 exp ! k k A A k  = =  定义: 函数矩阵指数函数 0 exp ! k k k A t At k  = =  它在 t 的任何有限区间内一致收敛的.因为当 k t c   0, 时 ! ! ! k k k k k A t k t k A c k A       2 1 . . 2! ! n x x x e x n = + + + + + 常系数线性微分方程组 而 收敛. ( ) 0 k k A c k  =  ∴ 一致收敛. 0 ! k k k A t k  = 

事条敷线性撒分方程组 xpA的性质 1.如果AB5则 exp(A+B)=exp A.exp B 证明：AB=BA,.二项式定理 (4+B)=A+k4-1B+kK-D4-2B2++B 2! m(a*)-含-宫(8++) 成立. ++++） (k-1): 会] 另一方面，由于级数 孕苹 p4m=会会)-[会 =exp(4+B) 结束 帮助■ 首页

结束 帮助 上一页 返回 下一页 目录 首页 * 1 . 如果 AB BA = , 则 exp exp .exp ( A B A B + =) 证明: ∵ AB BA = , ∴ 二项式定理 ( ) 1 2 2 ( 1) . 2 ! k k K k k k k A B A kA B A B B − − − + = + + + + 成立. ∴ ( ) ( ) ( ) 1 0 0 1 . ! ! exp k k k k K k A B B A kA B k A B k   − = = + + =  = + + + 1 2 2 0 . ! ( 1)! 2!( 2)! ! k k k k k A A B A B B k k k k  − − =   = + + + +     − − exp A的性质 常系数线性微分方程组 0 0 !( )! l k l k l A B l k l   − = =   =      − 另一方面,由于级数 与 绝对收敛. 0 ! k k A k  =  0 ! k k B k  =  0 0 exp .exp ! ! i j i j A B A B i j   = =    =         0 0 !( )! k l k l k l A B l k l  − = =   =      − = + exp( ) A B

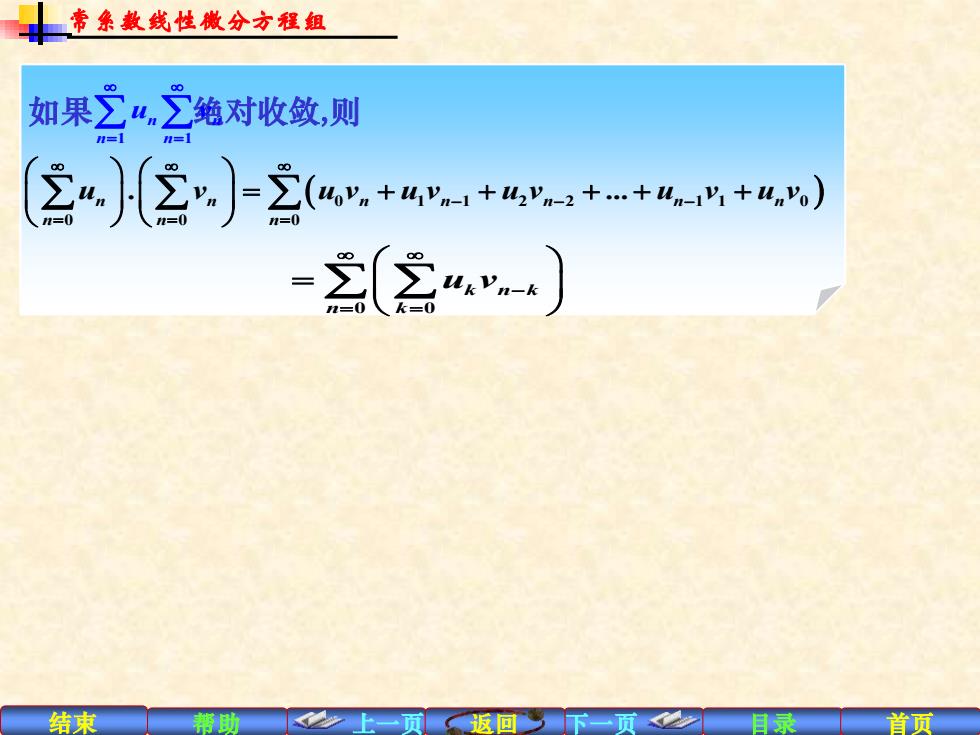
常朵教线性撒分方程组 如果∑“之绝对收敛，则 22-2 yn+41yn-1+42yn-2+.+4n-1y1+unyo） (会“) 结束 帮助 返回

结束 帮助 上一页 返回 下一页 目录 首页 如果 绝对收敛,则 1 1 n n n n u v   = =   ( 0 1 1 2 2 1 1 0 ) 0 0 0 . . n n n n n n n n n n u v u v u v u v u v u v    − − − = = =         = + + + + +        0 0 k n k n k u v   − = =   =       常系数线性微分方程组

常朵数线性微分方程组 2* 对于任何矩阵A,(exp存，且 (expA)=exp(-A) 事实上，由于与一可交换，所以 exp 4.exp(-4)=exp(4+(-A))=exp0=E 故 (exp )exp(-4) (若存在矩阵B,使AB=B,A則称是的逆.记为） 3 如果是非奇异矩阵，则 exp(T-AT)=T-(exp A)T. 证： eXP(T-AD-EAT k! =E+会T7=E+空行7 k ET+T之kT=T-(exp02 (由数学归纳可记(T-1AT)=T-AT. 结束 帮助 上一页返回下一页<2 目录 首页

结束 帮助 上一页 返回 下一页 目录 首页 * 2 对于任何矩阵A , ( 存在 ) ,且 1 exp A − ( ) 1 exp exp( ) A A − = − 事实上,由于 A 与 −可交换 A ,所以 exp .exp( ) exp( ( )) exp0 A A A A E − = + − = = 故 1 (exp ) exp( ) A A − = − （若存在矩阵 B ，使 AB BA E = = , 则称 是 的逆 B .记为 A ） 1 A − * 3 如果 是非奇异矩阵 T ,则 1 1 exp( ) (exp ) . T AT T A T − − = 证: 1 1 1 ( ) exp( ) ! k k T AT T AT E k  − − = = + (由数学归纳可记 ) 1 1 ( ) . k k T AT T A T − − = 1 1 1 1 ( ) ! ! k k k k T A T A E E T T k k   − − = = = + = +   1 1 1 1 ( ) (exp ) . ! k k A T ET T T T A T k  − − − = = + =  常系数线性微分方程组

常朵数线性微分方程组 下面讨论 x=Ax (5.33) 定理9.矩阵(t)=exp At是(5.33)的基阶矩阵，且满足(0)=E, 证明：(O)=exp0=E. (-(x)+ 12! (k-1): =Aexp At=Ad(t) (在任何有限区间expA致收敛) 这说明（建解矩阵又 detg(0)=det E=1. 因此，p5.33)的基解矩阵. 从而，(5.33)的任一解p(可表为 (t)=(exp At).c 结束 帮助 返回

结束 帮助 上一页 返回 下一页 目录 首页 下面讨论 ' x Ax = (5.33) 定理9. 矩阵 ( ) exp t At = 是(5.33)的基阶矩阵,且满足 (0) = E . 证明: (0) exp 0 . = = E 2 3 2 1 ' ' ( ) (exp ) . . 1! 2! ( 1)! k k A t A t A t t At A k  − = = + + + + + − = = A At A t exp ( )  (在任何有限区间 exp 一致收敛 At ) 这说明 ( )t 是解矩阵.又 det (0) det 1.  = = E 因此, ( ) 是 t (5.33)的基解矩阵. 从而,(5.33)的任一解 ( )t 可表为 ( ) (exp ). t At c = 常系数线性微分方程组

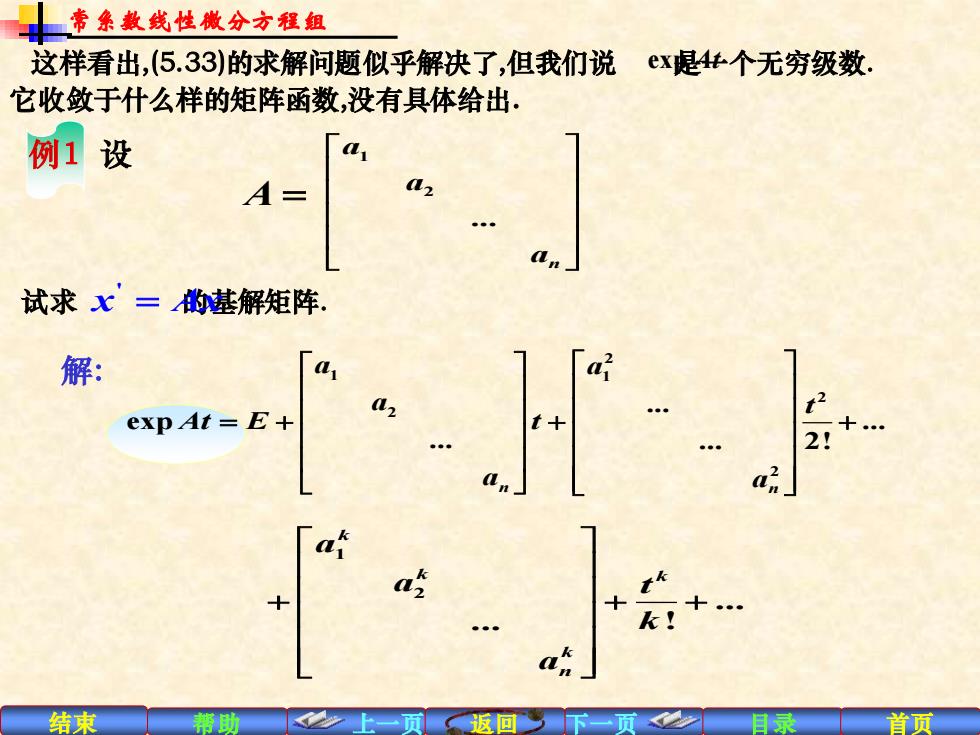
考条散线性微分方程组 这样看出，(5.33)的求解问题似乎解决了，但我们说ex是4：个无穷级数. 它收敛于什么样的矩阵函数，没有具体给出. 例1设 试求七=的基解矩阵。 解： exp At=E+ 2 t十 2 k! 结束 帮助 目录 首页

结束 帮助 上一页 返回 下一页 目录 首页 解: 2 1 1 2 2 2 . exp . . . 2 ! n n a a a t At E t a a             = + + +               1 2 . . ! k k k k n a a t k a     + + +           这样看出,(5.33)的求解问题似乎解决了,但我们说 是一个无穷级数. 它收敛于什么样的矩阵函数,没有具体给出. exp At 例1 设 1 2 . n a a a             A = 试求 的基解矩阵. ' x Ax = 常系数线性微分方程组

常票数线性微分方程组 2 k! 1+02t+.+ a0 十. k! 1+at+.+ (a,t)k k! 十. n 结束 帮助 返回

结束 帮助 上一页 返回 下一页 目录 首页 2 1 1 1 2 2 ( ) ( ) 1 . . 2! ! ( ) 1 . . ! . ( ) 1 . . ! k k k n n a t a t a t k a t a t k a t a t k     + + + + + + + + + = + + + +   1 2 . . n a t a t a t e e e     =         常系数线性微分方程组

常朵敷线性微分方程组 例2.试求 x的基解矩阵 解4[66[8小-4+4 eap- 8-88-88 PA00 结束 帮助 2上一贡返下一顶<2目录 首页

结束 帮助 上一页 返回 下一页 目录 首页 例2. 试求 ' x = 2 1 0 2 x       的基解矩阵. 解: 1 2 2 1 2 0 0 1 0 2 0 2 0 0 A A A       = = + = +             ∵ 2 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0                 = =         ∴ 2 2 2 0 1 1 exp 0 0 1 0 1 t t t e t t At e e      = =           常系数线性微分方程组 1 2 exp exp .exp At A t A t = 2 2 2 2 0 0 1 0 1 . 0 0 0 0 0 2! t t e t E t e           = + + +                  

事条数线性微分方程组 5.3.2基解矩阵的计算公式 三.基解矩阵的计算公式 由定理9知，方程X=的基解矩阵为 exp At=E+At+4't2 十。 2! k! 它虽然是收敛的，但是它的每一元素没有具体表出.下面再进一步讨论©曲At 计算 我们知道 衡的齐次线性方程是有指数函数的形式的解，由此得到启发，我们 设 p(t)=erc,c≠0 (5.43) 代入方程得 几etc=Aerc→er(E入-A)c=0→（入E-A)c=0. 即P()=533)的解的充分必要条件是及要湖足程 (孔E-A)c=0. (5.44) 是方程x=解.为待定的常向量，为待宠常数 结束 帮助 上一页返回

结束 帮助 上一页 返回 下一页 目录 首页 三. 基解矩阵的计算公式 由定理9知,方程 的基解矩阵为 ' x Ax = 2 2 exp . . 2! ! k k A t A t At E At k = + + + + + 它虽然是收敛的,但是它的每一元素没有具体表出.下面再进一步讨论 的 计算. exp At 我们知道 阶的齐次线性方程是有指数函数的形式的解,由此得到启发,我们 设 n ( ) , 0 t t e c c   = = (5.43) 常系数线性微分方程组 5.3.2 基解矩阵的计算公式 ( ) 0 ( ) 0. t t t e c Ae c e E A c E A c       =  − =  − = 代入方程得 即 ( ) 为(5.33)的解的充分必要条件是 及 要满足方程 t t e c   =  c ( ) 0. E A c − = (5.44) 是方程 的解. 为待定的常向量, 为待定常数. ' x Ax = c 