
§2.4一阶隐方程与参数表示 1.可对解出的方程y=Fcy). 例2.22 例2.23 2.可对x解出的方程x=Fy). 例2.24 3.方程不显含y的方程Fcy)=0 例2.25 例2.26 4.方程不显含x的方程Fy)=0. 例2.27 结束 帮助■ <上一扳回下一顶<■目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 §2.4 一阶隐方程与参数表示 1.可对y解出的方程 y=F(x,y ’). 2.可对x解出的方程 x=F(y,y ’). 3.方程不显含y的方程 F(x,y ’)=0. 4.方程不显含x的方程 F(y,y ’)=0. 例2.22 例2.23 例2.24 例2.27 例2.25 例2.26

上§2.4一阶隐方程与参数表示 讲授内容: 一阶隐方程F化,妙)=O的四种特殊类型方程的求解 讲授重点 x=f,y),F,y)=0,fy)=0的解法 难点: f,y)=0和FJy)=0的参数表示 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 一阶隐方程 F(x,y,y')=0 的四种特殊类型方程的求解. x=f(x,y’), F(x,y’)=0, f(y,y’)=0的解法 f(y,y’)=0 和F(x,y’)=0的参数表示. §2.4 一阶隐方程与参数表示 讲授内容: 讲授重点: 难点:

_§2.4一阶隐方程与参数表示 前面讲述的关于一阶方程的几种解法,都是对能把y明显解出而可 表示成标准形y'=x,y)进行的。但是若从一般形式方程Fx,y')=O 无法将y解出,或者即使能把y'解出来,其表达式非常复杂,那么上 述那些方法就无法使用.例如 e就无法将y表示出来.为 了求解这类方程,我们采用所谓的参数形式解.就是把它的解y=y(x)想 办法表示成 x=(t),y=w(t), 这里t为参数。 下面介绍四种特殊类型方程: 1.可对y解出的方程y=Fc). 2.可对x解出的方程x=F). 3.方程不显含y的方程Fxy=0. 4.方程不显含x的方程Fy)=0. 结束 返回下一页<目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 前面讲述的关于一阶方程的几种解法,都是对能把y ’明显解出而可 表示成标准形 y ’ = f(x,y) 进行的。但是若从一般形式方程F(x,y,y ’ )=0 无法将y ’解出,或者即使能把y ’解出来,其表达式非常复杂,那么上 述那些方法就无法使用.例如 就无法将y ’表示出来.为 了求解这类方程,我们采用所谓的参数形式解.就是把它的解y=y(x)想 办法表示成 ' 2 2 ' 1 y e xy + = 这里t 为参数。 x t y t = = ( ), ( ), 下面介绍四种特殊类型方程: 1.可对y 解出的方程 y=F(x,y ’). 2.可对x 解出的方程 x=F(y,y ’). 3.方程不显含y 的方程 F(x,y ’)=0. 4.方程不显含x 的方程 F(y,y ’)=0. §2.4 一阶隐方程与参数表示

S2.4一阶隐方程与参数表示 1.可对y解出的方程y=Fxy 对于方程y=八x,美有选续偏导数,引进参数 =p dx 于是有y=f(x,p两边对x求导,得 a af of dp p Oxc O ap dx af op 这是关于x,p的一阶微分方程,导数已解出.可按前而讲的方法求出 解,假设通解为Φ(x,p,c=0,则原方程的通解为 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 对于方程 ( , ) ,其中f有连续偏导数,引进参数 dy y f x dx = ( ) dy p x dx = 1.可对y 解出的方程 y=F(x,y ’). f f dp p x p dx = + f p dp x dx f p − = 这是关于x,p的一阶微分方程,导数已解出.可按前而讲的方法求出 解,假设通解为(x,p,c)=0, 则原方程的通解为 §2.4 一阶隐方程与参数表示 于是有 y f x p = ( , ) , 两边对x求导,得

L§2.4一阶隐方程与参数表示 例2.22解方程 解:令 =p,则原方程变为y=p+2 两边对x求导得 p=n黑2p+2密 pd+(3p2+2x)dp=0 aM =1, aN a =2 或这写成 3p2dp+2xdp+pdx =0 1-2 1 =十 两端乘P得 -P +p 3pdp+2xpdp+p'dx =0 L(p)=P 从而 4(匠p+p2)=0 3 n2+2=c→x= c- 其中c为任意的常数.故原方程的通解为 (p≠0) 2c .·p=0时,y=0.y=0也是解. 结束 籍助2上一贡返回下 首页
结束 帮助 上一页 返回 下一页 目录 首页 例2.22 解方程 3 ( ) 2 0. dy dy x y dx dx + − = 解: 令 dy p dx = ,则原方程变为 3 y p xp = + 2 两边对x求导得 2 3 2 2 dp dp p p p x dx dx = + + 或这写成 2 3 2 0 p dp xdp pdx + + = 两端乘P得 3 4 2 ( ) 0 4 从而 d p xp + = 4 4 2 2 3 3 4 4 c p p xp c x p − + = = 3 2 3 2 0 p dp xpdp p dx + + = §2.4 一阶隐方程与参数表示 2 pdx p x dp + + = (3 2 ) 0 1 2 M N P x = = , 1 2 1 p p − = + − + ( ) p p = 其中c为任意的常数. 故原方程的通解为 2 2 3 3 4 0 2 1 2 c x p p p c y p p = − = − ,( ) p y y = = = 0 0 0 时, 也是解

上§2.4一阶隐方程与参数表示 例侧223求方程y=(-x号 ⑨,2 dx 的通解。 解图令农=p,则原方程变为 d y=pp+ (2.40) 2 两边对x求导得p=2p dx +x或者写成 2-102p-)=0 由此即得 -1=0,或2p-x=0,由虫-1=0→p=x+c dx 代入(2.40)得通解 +cx+c2(1.41) 2 由2p-x=0,得,代2.41)得另一个解 (2.42) 4 考虑(2.41)与(2.42)之间的关系.解方程组 Fcx+c2 2 得交点坐标(c,c) A 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 例2.23 求方程 的通解. 2 2 ( ) 2 dy dy x y x dx dx = − + 解: 令 dy p dx = ,则原方程变为 = − + 2 2 (2.40) 2 x y p xp 两边对x求导得 2 dp dp p p p x x dx dx = − − + 或者写成 ( 1)(2 ) 0 dp p x dx − − = §2.4 一阶隐方程与参数表示 由此即得 1 0 2 0 dp p x dx − = − = ,或 , 代入(2.40)得通解 由 − = = + 1 0 dp p x c dx = + + 2 2 (1.41) 2 x y cx c 由 2 0 ,代入 2 (2.41)得另一个解 x p x p − = = ,得 = 2 (2.42) 4 x y 考虑(2.41)与(2.42)之间的关系. 解方程组 2 2 2 2 4 x y cx c x y = + + = 得交点坐标 2 ( ) c c
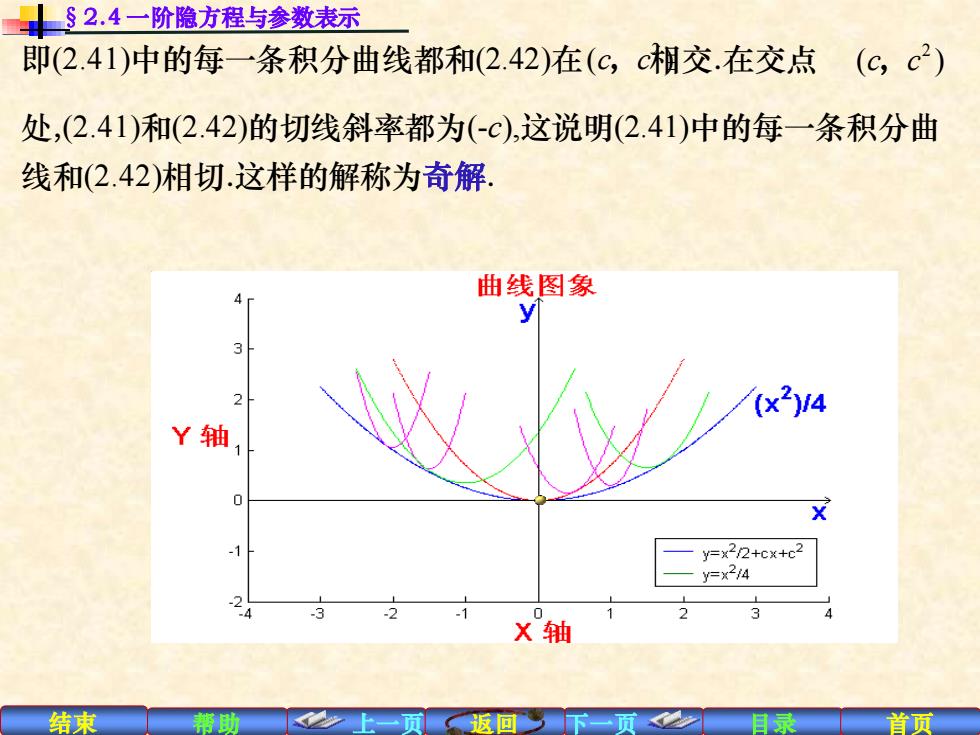
§2.4一阶隐方程与参数表示 即(2.41)中的每一条积分曲线都和(2.42)在(c,c相交.在交点(c,c2) 处,(2.41)和(2.42)的切线斜率都为(-c),这说明(2.41)中的每一条积分曲 线和(2.42)相切.这样的解称为奇解 曲线图象 3 (x2)4 Y轴 y=x2/2+cx+c2 y=x24 3 X轴 结束 上一贡同下一<2■ 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 即(2.41)中的每一条积分曲线都和(2.42)在 相交.在交点 处,(2.41)和(2.42)的切线斜率都为(-c),这说明(2.41)中的每一条积分曲 线和(2.42)相切.这样的解称为奇解. §2.4 一阶隐方程与参数表示 2 ( ) c c , 2 ( ) c c , 4 2 x y = x y o

S2.4一阶隐方程与参数表示 2.可对x解出的方程x=Fyy). 对方程x=f0,黑其中f0,集有连续偏导数。 令=,则原方程变为 x=f(y,p) (2.43) 现我们只要将P用xy表示出来代入(2.43)或得到关系式Φ(y,p)=0 则可得(2.43)的解.(2.43)两端对y求导得 众。影+影器 1 af 这是关于,p的一阶微分方程,它的导数可解出: p ay(2.44) a 若(2.44)的通解为:Φ(Jy,p,C)=0 ap 则(2.43)的通解为 x=f(y,p) lΦ(y,p,c)=0 其中c为任意常数. 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 §2.4 一阶隐方程与参数表示 2.可对x解出的方程 x=F(y,y ’). 对于方程 ( , ) 其中 具有连续偏导数. dy x f y dx = ( , ) dy f y dx 令 , 则原方程变为 dy p dx = x f y p = ( , ) (2.43) 现我们只要将P用x,y表示出来代入(2.43)或得到关系式 则可得(2.43)的解. = ( , ) 0 y p (2.43)两端对y求导得 dx f f dp 1 dy p y p dy = = + 这是关于y,p的一阶微分方程,它的导数可解出: − = (2.4 ) 1 4 f dp p y dy f 若(2.44)的通解为: = ( , , ) 0 y p c p 则(2.43)的通解为 ( , ) ( , , ) 0 x f y p y p c = = 其中c为任意常数.

§2.4一阶隐方程与参数表示 例2.24求方程(y')3+2y'-y=的通解. 解:解出x,令y=得 x=y-p3 2P (p≠O)两边对y求导得 、 03p密-(w-p密 'dy 即 p 2p2 pdy ydp+2pdp=O 于是 py)+d2p')=0 从而 2p+p=c→y=Cp ,因此 c-p-p x= 2p c-3p4 所以原方程通解为 2p 4p2 c 3 x=- p (P≠0) P y= 此外,还有特解=0. 2p 结束 帮助 返回下而< 首页
结束 帮助 上一页 返回 下一页 目录 首页 例2.24 求方程 的通解. 3 ( ') 2 ' 0 y xy y + − = 解: 解出x,令 y' = 得 p − = 3 ( 0) 2 y p x p p 两边对y求导得 2 2 3 2 (1 3 ) ( ) 1 p dy dp y p dy dp p p p − − − = 2 0 3 pdy + ydp + p dp = 即 §2.4 一阶隐方程与参数表示 于是 ) 0 2 1 ( ) ( 4 d py + d p = 从而 yp + p = c 4 2 4 2 c p y p − = , 因此 2 4 3 4 4 3 2 2 p c p p p p c p x − = − − = 所以原方程通解为 2 2 3 3 4 4 ( 0) 2 2 c x p p p c p y p = − = − 此外,还有特解 y=0.

§2.4一阶隐方程与参数表示 3.方程不显含y的方程Fy=0. 对于方程,这是(x,y)平面上的一条曲线,我们想办法把它用参数表 示出来.令y=得 F(x,p)=0(2.45) 我们取(2.45)的适当形式的参数式: 注 x=p(t),p=v(t) (t为参数) p(t),W(t)怎么取要看方程的特点,否则方程会变得更复杂) 在(2.45)的任一条积分曲线上恒有=p 而欣=p'(t)t,所以 dy =v(t)y'(t)dt. 于是得到(2.45)的参数形式的通解: x=p(t) y=∫yw(t)p'dt+c 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 3.方程不显含y的方程 F(x,y ’)=0. F x p ( , ) 0 = (2.45) 我们取(2.45)的适当形式的参数式 : x t p t t = = ( ), ( ) ( ) 为参数 在(2.45)的任一条积分曲线上恒有 dy pdx = 而 dx t dt = '( ) ,所以 dy t t dt = ( ) '( ) . 于是得到(2.45)的参数形式的通解: ( ) ( ) ' x t y t dt c = = + §2.4 一阶隐方程与参数表示 ( ), ( ) t t ( 怎么取要看方程的特点,否则方程会变得更复杂) 注 对于方程, 这是 平面上的一条曲线,我们想办法把它用参数表 示出来.令 , 得 ( , ) x y y p =