
常微分方程多媒体教学课件 §4.2常系数线性方程的解法 主要内容 (一) 引言 (二) 复值函数与复值解 (三) 常系数齐线性方程和Euler方程 ★(总结)★(练习题) (四)非齐线性方程组与比较系数法 (五)作业 单击《所选的内容》打开目录再次单击关闭目录 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 常微分方程多媒体教学课件 §4.2 常系数线性方程的解法 主要内容 单击《所选的内容》打开目录再次单击关闭目录 (一) 引言 (二) 复值函数与复值解 (三) 常系数齐线性方程和E u l e r 方程 (五) 作业 ★ (总结) (四)非齐线性方程组与比较系数法 ★ (练习题)

引言 线性方程组的通解结构,从理论上讲,已得到彻底的解决。 但是求方程通解的方法还没有具体给出.对于一般线性方程 是没有普遍的解法的.当方程的系数4,(t)均为系数时,它 的求解问题已得到彻底解决.在求常系数齐次线性方程通解 的方法前,我们先引进复值函数及复值解的概念, 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 引言 线性方程组的通解结构,从理论上讲,已得到彻底的解决. 但是求方程通解的方法还没有具体给出.对于一般线性方程 是没有普遍的解法的.当方程的系数 a t i ( ) 均为系数时,它 的求解问题已得到彻 底解决.在求常系数齐次线性方程通解 的方法前,我们先引进复值函数及复值解的概念.

(一)复值函数与复值解 如果对区间a≤t≤b中的每一实数t有复数(t)=p(t)+(t) 与它对应,其中p(t)和(t)是区间a≤t≤b上定义的实函数,i 是虚数单位,我们就说在区间α≤t≤b上给定了一个复值函数 z(咖果实函数p(t),(t)当趋丁时有极限,我们就称复值 z(t) 当t趋于t时有极限并且定义 lim(t)=limg(t)+ilim(t) t→to t-→to t→to 如果1imz()=(4)我们就称z(t)在t,连续.显然z(在连续, 相当于p(t),(t)在t连续,当z(t)在区间a≤t≤b上每点都连续 时,就称z(t)在区间M≤t≤b上连续.如果极限 lim z(t)-(t) t-→t t-to 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 (一)复值函数与复值解 如果对区间 a t b 中的每一实数t 有复数 z t t i t ( ) ( ) ( ) = + 与它对应,其中 ( ) ( ) t t 和 是区间 a t b 上定义的实函数, i 是虚数单位,我们就说在区间 a t b 上给定了一个复值函数 z t( ).如果实函数 ( ), ( ) t t t t 当 趋于 时有极限 0 ,我们就称复值 z t( ) 当 0 t趋于t 时有极限并且定义 0 0 0 lim ( ) lim ( ) lim ( ) t t t t t t z t t i t → → → = + 如果 , 我们就称 在 连续.显然 在 连续, 0 0 lim ( ) ( ) t t z t z t → = z t( ) ( ), ( ) t t 0 t 时,就称 在区间 a t b 上连续.如果极限 相当于 在 连续,当 在区间 上每点都连续 z t( ) z t( ) z t( ) 0 t 0 t a t b 0 0 0 ( ) ( ) lim t t z t z t → t t − −

存在,就称z(t)在t有导数(可微),且记此极限为 z'(t) dt 显然z(t)在t。处有导数相当于p(t),(t)在t处有导数,且 k()=lp)+i) dt dt d 如果(t)在a≤t≤b上每一点都有导数,就称z(t)在区间a≤t≤b 上有导数.对于高阶导数可以类似地定义.设,(),2()是定义 在a≤t≤b上的可微函数,C是复值函数,容易验证下列等式成立: 品0+o1-省 dt dt eo1-e0 dt 0-n=20+a色 在讨论常系数线性方程时,函数K,将起着重要的作用,这里歌 是复值常数.我们现在给出他的定义,并且讨论它的简单性质 设k=α+iB是任一复数,这里,B是实数,而t为实变量. 结束 首而
结束 帮助 上一页 返回 下一页 目录 首页 存在,就称 在 有导数(可微),且记此极限为 或 显然 在 处有导数相当于 在 处有导数,且 0 dz t( ) dt 0 z t ( ) z t( ) z t( )0 t 0 t 0 ( ), ( ) t t t 0 0 0 dz t d t d t ( ) ( ) ( ) i dt dt dt = + 如果 z t( ) 在 a t b 上每一点都有导数,就称 在区间 上有导数.对于高阶导数可以类似地定义.设 是定义 z t( ) a t b 在 上的可微函数, 是复值函数,容易验证下列等式成立: 1 2 z t z t ( ), ( ) a t b c 1 2 1 2 ( ) [ ( ) ) ( ) ( ] dz t dz t dt d z t z t dt dt + = + 1 1 [ ( )] d d ( ) cz t d z t t c dt = 1 2 1 2 2 1 ( ) ( ) [ ( ) ( )] . ( ) ( ). dz t dz t z t z t d d z t z t dt t dt = + 在讨论常系数线性方程时,函数 将起着重要的作用,这里 设 是任一复数,这里 是实数,而 为实变量. kt e k k i = + , t 是复值常数.我们现在给出他的定义,并且讨论它的简单性质

我f们定义ek,=ea+ir=e(cos Bt+isin Bt) 由上述定义立即推得: csp()sin) 如果以k=a+iB表示复数k=a+ip的共复数.那么容易证明 eki ekr 此外,函数e“还有下面重要性质 (1))要e1tk)r=ek1t.et 事实上,记k1=必1+iP,k2=必2+p2那么由定义得到 e(kitka)t =e(ataa)tti() =ea+a,[cos(月+P2)t+isin(月+B2)t川 Btc B,t-sin B,tsin B,t)+i(sin BtcBtcBtB.t) =e'(cosP,t+isin阝,t)e'(cos B,t+-isin B2t) =ehitekat 结束 帮助
结束 帮助 上一页 返回 下一页 目录 首页 我们定义 ( ) (cos sin ) kt i t t e e e t i t + = = + 由上述定义立即推得: 如果以 k i = + 表示复数 k i = + 的共复数.那么容易证明 kt kt e e = 此外,函数 还有下面重要性质 重要性质: kt e 1 2 1 2 ( ) k k t k t k t e e e + (1) = 1 cos ( ), 2 i t i t t e e − = + 1 sin ( ) 2 i t i t t e e i − = − 事实上,记 k i k i 1 1 1 2 2 2 = + = + , 那么由定义得到 1 2 1 2 1 2 (k k t) ( )t i( ) e e + + + + = 1 2 ( ) 1 2 1 2 [cos( ) sin( ) ] t e t i t + = + + + 1 2 ( ) 1 2 1 1 1 1 1 2 [(cos cos sin sin ) (sin cos cos sin )] t e t t t t i t t t t + = − + + 1 2 1 1 2 2 (cos sin ) (cos sin ) t t e t i t e t i t = + + 1 2 k t k t = e e

( =ker其中t为实变量 事实上设k=ax+iB,则 dek dt -e1=ee) _dt _dt dear iBt +ear de dt dt -aee4 (sin Bi+cos Bt) dt -ae(atip)+ea(-Bsin Bt+iB cos Bt) -ae +iBeaein=(a+iB)e=ke (3) 来er=4e 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 (2) 其中 为实变量 kt de kt ke dt = t 事实上,设 k i = + ,则 ( ) [ ] ( ) i t kt d d t i t e e de dt e dt dt + = = i t i t t de de t e e dt dt = + (sin cos ) t i t t d e e e t t dt = + + ( ) ( sin cos ) i t t e e t i t + = + − + ( ) kt t i t kt kt = + = + = e i e e i e ke (3) ( ) n kt n kt n d e k e dt =

现在我们引进线性方程的复值解的定义.定义于区间α≤t≤b 上的实变量复值函数x=(t)称为方程(4.1)的值解如果 0+a0+a产0 d"t du-2t +n-o8+a.00=0) 对于a≤t≤b恒成立. 结束 帮助
结束 帮助 上一页 返回 下一页 目录 首页 现在我们引进线性方程的复值解的定义.定义于区间 上的实变量复值函数 称为方程 (4.1) 的值解如果 a t b x z t = ( ) ( ) 1 2 1 2 1 2 1 ( ) ( ) ( ) ( ) ( ) . ( ) ( ) ( ) ( ) n n n n n n n n d z t d z t d z t a t a t d t d t d t dz t a t a t z t f t dt − − − − − + + + + + 对于 a t b 恒成立.

定理8:如果方程(4.2)中所有系数4(t)(i=1,2,n) 都是实值函数,而x=z(t)=p(t)+i(t)是方程的复值 解,则z(的实部p(t),虚部和共轨复值函数 (t) 也都是方程(42)的解 证明设xz行=p(t)+()是方程(4.2)的复值解,则代入 方程得 [(t)+i(t)]+a (t)(t)+ig(t)]+ .+an(t)lp(t)+igp(t)]≡0 而1pm())+a,(t)pn-())+.+an()(川+ iLpm(t)+a,(t)pn-(t)+.+an(t)p(t川≡0 g((t)+a (t)o(-1()+.+a,()()]=0 由此得 pm)(t)+a1(t)pm-(t)+.+an(t)p(t)=0 结束 上一贡返回下页 首页
结束 帮助 上一页 返回 下一页 目录 首页 定理8:如果方程 中所有系数 都是实值函数,而 是方程的复值 解,则 的 和共轨复值函数 (4.2) ( )( 1,2,., ) a t i n i = x z t t i t = = + ( ) ( ) ( ) z t( ) 实部 ( ) ( ) t t ,虚部 z t( ) 也都是方程(4.2)的解. 证明:设 是方程(4.2)的复值解,则代入 方程得 x z t t i t = = + ( ) ( ) ( ) ( ) ( 1) 1 [ ( ) ( )] ( )[ ( ) ( )] n n t i t a t t i t − + + + + . . + + a t t i t n ( )[ ( ) ( )] 0 而 ( ) ( 1) 1 [ ( ) ( ) ( ) . ( ) ( )] n n n t a t t a t t − + + + + ( ) ( 1) 1 [ ( ) ( ) ( ) . ( ) ( )] 0 n n n i t a t t a t t − + + + 由此得 ( ) ( 1) 1 [ ( ) ( ) ( ) . ( ) ( )] 0 n n n t a t t a t t − + + + = ( ) ( 1) 1 ( ) ( ) ( ) . ( ) ( ) 0 n n n t a t t a t t − + + + =

由上面证明式说明中(利pt)的解),同理可证 (t)+i图的4.2) 结束 帮助
结束 帮助 上一页 返回 下一页 目录 首页 也是 的解。 由上面证明式说明 ( )t 和 是 ( )t 的解 (4.2) ,同理可证 (4.2) ( ) ( ) t i t +
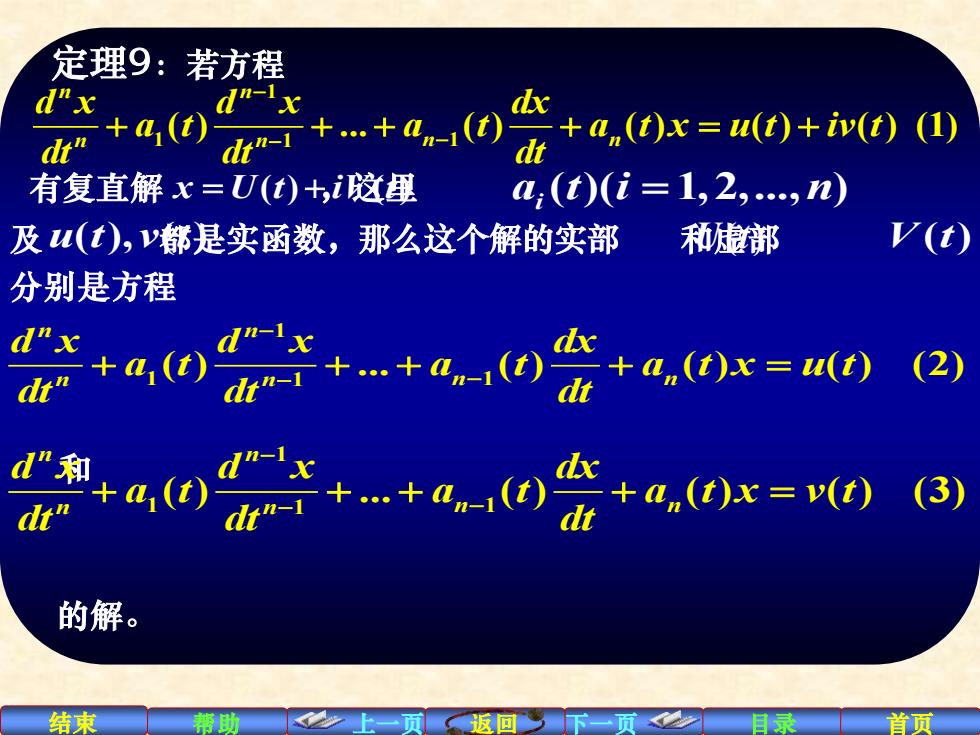
定理9:若方程 d"x d"-Ix dx +a(t) dt" dri+.+an-() +a,(t)x=u(t)+iv(t)(1) dt 有复直解x=U(t)+,这里 4,(t)(i=1,2,n) 及(t),都是实函数,那么这个解的实部 和虚部 V(t) 分别是方程 dx dt" )(2) )(3) 的解。 结束 上一贡扳同下一<2 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 和 1 1 1 1 ( ) . ( ) ( ) ( ) (3) n n n n n n d x d x dx a t a t a t x v t dt dt dt − + + + + = − − 的解。 1 1 1 1 ( ) . ( ) ( ) ( ) (2) n n n n n n d x d x dx a t a t a t x u t dt dt dt − + + + + = − − 定理9:若方程 1 1 1 1 ( ) . ( ) ( ) ( ) ( ) (1) n n n n n n d x d x dx a t a t a t x u t iv t dt dt dt − + + + + = + − − 有复直解 x U t iV t = + ( ) ( ) ,这里 ( )( 1,2,., ) a t i n i = 及 u t v t ( ), ( ) 都是实函数,那么这个解的实部 和虚部 U t( ) 分别是方程 V t( )