
线性微分方程组 §5.2.线性微分方程组的一般理论 5.2.1齐线性微分方程组 现在讨论线性微分方程组 x=A(t)x+f(t) (5.14) 的一般理论,主要是它的解的结构问题 如果f(t)专则(5.14)称为非齐线性的 如果f(),号则方程的形式为 x=(t)x (5.15) 现讨论(5.14)的通解结构问题, 一.齐次线性方程组 设A(在区间α≤是连续的. 定理2.如果u(利 是)5.15)的解,则它们的线性组合. cu(t)+炮是符.15)的解.这里 是常数,B 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 如果 f t( ) 0 ,则( 5.14)称为非齐线性的. §5.2. 线性微分方程组的一般理论 现在讨论线性微分方程组 ' x A t x f t = + ( ) ( ) (5.14) 的一般理论,主要是它的解的结构问题. 线性微分方程组 5.2.1 齐线性微分方程组 如果 f t( ) 0 ,则方程的形式为 ' x A t x = ( ) (5.15) 现讨论(5.14)的通解结构问题. 一. 齐次线性方程组 设 A t( ) 在区间 a t b 上是连续的. 定理2. 如果 和 是(5.15)的解,则它们的线性组合. 也是(5.15)的解.这里 是常数. u t( ) v t( ) u t v t ( ) ( ) +

线性微分方程组 为了研究(5.15)的解的结构,下面引进向量函数序列线性 相关与线性无关的概念 设飞(t),是义在 止的≤仍向量函数: 如果存在不全为零的常数C1,Cn·使得 CX(t)+.+cnxn(t)=0在a≤t≤h恒成立 则称向量函x(),套()线曲相关,否则称 飞1(t),球t)上俄懂无关 结束 籍助2上一贡意下一页<2目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 为了研究(5.15)的解的结构,下面引进向量函数序列线性 相关与线性无关的概念. 设 是定义在 上的 个向量函数. 1 ( ),., ( ) n x t x t a t b n 如果存在不全为零的常数 1 ,., . c cn 使得 1 1 c x t c x t ( ) . ( ) 0 + + n n 在 a t b 上恒成立. 则称向量函 在 上线性相关,否则称 在 上线性无关. 1 ( ),., ( ) n x t x t [ , ] a b 1 ( ),., ( ) x t x t n [ , ] a b 线性微分方程组

存在唯一性定理的一般理论 例1.向量函数 1 0 x(t)= 】 在任何区间线性无关.(k>O) 解, .Cx(t)+.+Cnxn(t)≡0→c0+ct++ct=0 t∈[a,b] 由于1,t,.在茌何区间线性无关. ∴.c:≡0.(i=1,2,.) 故x(t),饿性无关 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 例1.向量函数 1 1 0 ( ) : 0 x t = 2 0 ( ) : 0 t x t = 2 3 0 ( ) : 0 t x t = 4 0 ( ) : 0 k t x t = 在任何区间线性无关. ( ) k o 解:∵ 1 1 c x t c x t ( ) . ( ) 0 + + n n 0 1 . 0 k k c c t c t + + + t a b [ , ] ∴ 0.( 1, 2,.) i c i = 故 1 线性无关. ( ),., ( ) x t x t k 1, ,., k 由于 t t 在任何区间线性无关. 存在唯一性定理的一般理论

线性微分方程组的一般理论 cos" sin2t-1 X1= 在任何区间线性相关. 因为取c1=1,c2=}则 Cx1(t)+C2x2(t)= -0 例. 00:0 x1= 结束 露用 返回下而< 首页
结束 帮助 上一页 返回 下一页 目录 首页 又 , 1 x = 2 cos 0 : 0 t 2 x = 2 sin 1 0 : 0 t − 在任何区间线性相关. 因为取 c c 1 2 = = 1, 1 ,则 1 1 2 2 0 0 ( ) ( ) 0 : 0 c x t c x t + = = 例. 3 6 3 6 1 2 3 6 , 2 t t t t t t e e x e x e e e = = − 在 (− + , 上线性无关 ) . 线性微分方程组的一般理论
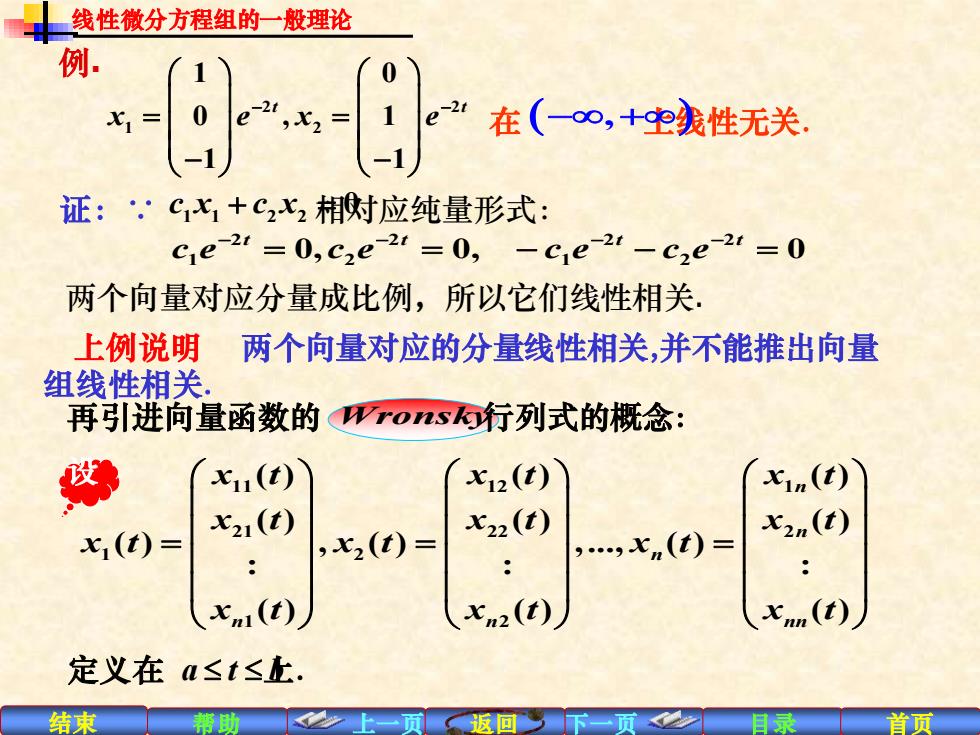
线性微分方程组的一般理论 例 69 在(∞,+空麦性无关 证:.C火1+C2x2相对应纯量形式: C1e21=0,c2e2=0, -ce 2-cze-2 =0 两个向量对应分量成比例,所以它们线性相关. 上例说明 两个向量对应的分量线性相关,并不能推出向量 组线性相关 再引进向量函数的Wros行列式的概念: x11(t) X12(t) xin(t) x21(t) x22(t) x1(t)= x2n(t)) ,x2(t)= .xn(t)= : xm1(t) 、七n2(t) xn (t) 定义在a≤t≤正, 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 例. 2 2 1 2 1 0 0 , 1 1 1 t t x e x e − − = = − − 在 ( 上线性无关 ) . − + , 证:∵ c x c x 1 1 2 2 + = 相对应纯量形式 0 : 2 2 2 2 1 2 1 2 0, 0, 0 t t t t c e c e c e c e − − − − = = − − = 两个向量对应分量成比例,所以它们线性相关. 上例说明 两个向量对应的分量线性相关,并不能推出向量 组线性相关. 再引进向量函数的 Wronsky 行列式的概念: 11 12 1 21 22 2 1 2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) , ( ) ,., ( ) : : : ( ) ( ) ( ) n n n n n nn x t x t x t x t x t x t x t x t x t x t x t x t = = = 设 定义在 a t b 上. 线性微分方程组的一般理论

一线性微分方程组的一般理论 称行列式 11 X12 W[x(t),xn(t)]= X21 X22 2n Xn2 Xnn 为这个向量函数的Wro你式, 定理3.如果向量函数七(t),在区间 线性相关,则 它们的 行列残nsy WV(t)=0,a≤t≤b 证明:由假设可知存在不全为零的常数C,C2,使得 C1X1(t)+C2x2(t)+.+Cnxn(t)≡0,a≤t≤b (5.16) 把(5.16)看成是以c1,c2.为朱知量的齐次线性代数方程 组,这方程组的系数行列式就是 x1(t),的伏朝斯 基行列式 ·W(t) 由齐次线性代数方程组的理论知道,要此方程组有非零解。 结束 上一面回下一页< 首页
结束 帮助 上一页 返回 下一页 目录 首页 定理3. 如果向量函数 在区间 上线性相关,则 它们的 行列式 1 ( ),., ( ) x t x t n a t b Wronsky W t a t b ( ) 0, 证明:由假设可知存在不全为零的常数 1 2 , ,., 使得 n c c c 1 1 2 2 ( ) ( ) . ( ) 0, n n c x t c x t c x t a t b + + + (5.16) 把(5.16)看成是以 为未知量的齐次线性代数方程 组,这方程组的系数行列式 就是 的伏朗斯 基行列式 . 1 2 , ,., c c cn 1 ( ),., ( ) x t x t n W t( ) 由齐次线性代数方程组的理论知道,要此方程组有非零解. 称行列式 11 12 1 21 22 2 1 1 2 . . ( ),., ( ) : : . : . n n n n n nn x x x x x x W x t x t x x x = 为这 n 个向量函数的 Wronsky 行列式. 线性微分方程组的一般理论

线性微分方程组的一般理论 则它的系数行列式应为零,即 W(t)=0,a≤t≤b 定理证毕 设x(),是⑥,15)的个解如果存在某个 ,t。to∈[a,b] 使得1 W[x(o),测理3.推出 七(t)在,n(t让线 性无关再有定理4.推出 WIx(t),xn(t)川≠0,t∈[a,b] 所以(5.15)的个解的wro行例式 或嗜恒等于零,或者处处 不等于零 定理5.(5.15)一定存在线性无关的解,称(5.15)的个线 性无关的解为(5.15)的一个基本解组.(5.15)有无穷多个基本解 组. 定理6,如果x(t),.是55)的个线性无关的解, 则(5.15)的任一解x(t均可表为 xt)=Cx(t)+.+Cnxn().≥ (5.20) 其中c:,(i=1,2是相应的确定常数, 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 1 0 0 W x t x t ( ),., ( ) 0 n = [ , ] a b 设 是(5.15)的 个解,如果存在某个 , 使得 .则由定理3.推出 在 上线 性无关.再有定理4.推出 1 ( ),., ( ) n x t x t n 0 t 0 t a b [ , ] 1 ( ),., ( ) n x t x t 1 [ ( ),., ( )] 0, [ , ] W x t x t t a b n = 定理5. (5.15)一定存在 个线性无关的解,称(5.15)的 个线 性无关的解为(5.15)的一个基本解组.(5.15)有无穷多个基本解 组. n n 定理6. 如果 是(5.15)的 个线性无关的解, 则(5.15)的任一解 均可表为 1 ( ),., ( ) x t x t n n x t( ) 1 1 ( ) ( ) . ( ). x t c x t c x t = + + n n (5.20) 其中 ,( 1, 2,., ) 是相应的确定常数. c i n i = 所以(5.15)的 个解的 行列式 或者恒等于零,或者处处 不等于零. n Wronsky W t( ) 线性微分方程组的一般理论 则它的系数行列式应为零,即 W t a t b ( ) 0, 定理证毕

定理4如果(5.15)的解x,(t),x2(t),xn(t)线性无关,那么 它们的伏朗斯基行列式W(t)=O,a≤t≤b, 证明我们采用反证法.设有某一个to,a≤得影 W(t,)=0 .考虑下面的齐次线性代数方程组: cx(to)+c2x2(to)+.+cx(to)=0 (5.17) 它的系数行列式就是W(,因为W(,=0, 所以(5.17)有非零解 .C1,C2,Cn以这个非零解构成向量函数 x(t)=x(t)+2x2(t)+.+(t) (5.18) 根据定理2,易知x(t)是(5.15)的解.注意到(5.17), 知道这个解x(t)满足初始条件 x(to)=0 (5.19) 但是,在a≤t圭恒等于零的向量函数0也是(5.15)的 满足初始条件(5.19)的解.由解的唯一性,知道 x(t慨0 cx(t)+c2x2(t)+.+cnxn(t)=0,a≤t≤b 结束 帮助 上一贡返回下页<2 首页
结束 帮助 上一页 返回 下一页 目录 首页 定理4 如果(5.15)的解 x ( t ), x ( t ),., x ( t ) 1 2 n 线性无关,那么 它们的伏朗斯基行列式 W ( t ) 0,a t b. = 证明 我们采用反证法.设有某一个 t ,a t b 0 0 ,使得 W ( t ) 0 0 = .考虑下面的齐次线性代数方程组: c x ( t ) c x ( t ) . c x ( t ) 0 1 1 0 2 2 0 n n 0 + + + = (5.17) 根据定理2,易知 x(t)是(5.15)的解.注意到(5.17), 知道这个解x(t)满足初始条件 x( t ) 0 0 = (5.19) 它的系数行列式就是 ,因为 ,所以(5.17)有非零解 . 以这个非零解 构成向量函数 W ( t ) 0 W ( t ) 0 0 = x( t ) c x ( t ) c x ( t ) . c x ( t ) + + + 1 1 2 2 n n (5.18) 1 2 n c ,c ,.,c 但是,在 上恒等于零的向量函数0也是(5.15)的 满足初始条件(5.19)的解.由解的唯一性,知道 ,既 a t b x( t ) 0 c x ( t ) c x ( t ) . c x ( t ) 0,a t b 1 1 2 2 n n + + +

应为c1,c2,c,不全为零,所以x,(t),x,(t,xn(t)线性相关 这就与线性无关的假设矛盾.定理得证 结束 帮助
结束 帮助 上一页 返回 下一页 目录 首页 这就与线性无关的假设矛盾.定理得证 应为c ,c ,.,c , x ( t ), x ( t ),.x ( t ) 1 2 n 1 2 n 不全为零 所以 线性相关
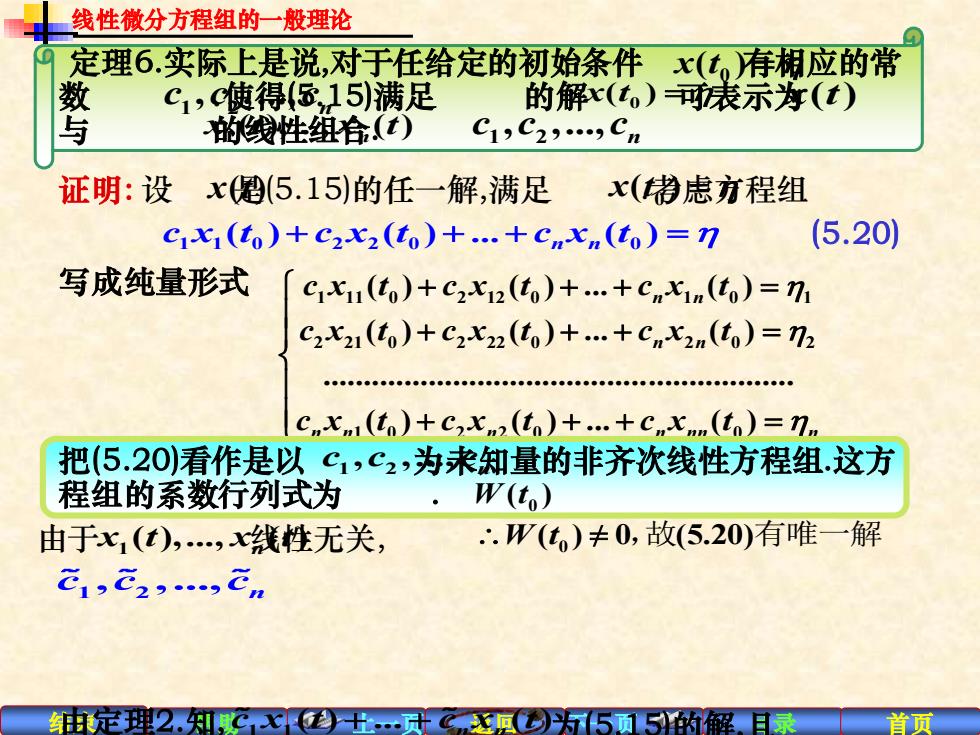
线性微分方程组的一般理论 0 定理6.实际上是说,对于任给定的初始条件x(t存相应的常 C,c使得(,15)满足的解x()可表示为(t) 的线性组合.(t)C1,C2,Cm 证明:设x(5.15)的任一解,满足 x(精虑亦程组 cx(to)+c2x2(to)+.+cnx(to)=n (5.20) 写成纯量形式 cx(to)+c2x12(to)+.+cnxin(o)=m C2x21(to)+C2x22(t)+.+Cnx2n(to)=72 Cx()+cx(o)+.+cx()=n 把(5.20)看作是以c1,c2,为求知量的非齐次线性方程组.这方 程组的系数行列式为 。 W(t) 由于x(t),线性无关, ∴.W(t)≠0,故(5.20)有唯一解 E1,E23.En 由定理2.知Cx十.武C顶为5顶5药解日录 首页
结束 帮助 上一页 返回 下一页 目录 首页 0 x t( ) = 1 2 , ,., n c c c 定理6.实际上是说,对于任给定的初始条件 有相应的常 数 .使得(5.15)满足 的解 可表示为 与 的线性组合. 0 x t( ) = x t( ) 1 ( ),., ( ) x t x t n 1 2 , ,., n c c c 证明: 设 x t( ) 是(5.15)的任一解,满足 .考虑方程组 0 x t( ) = 1 1 0 2 2 0 0 ( ) ( ) . ( ) n n c x t c x t c x t + + + = (5.20) 写成纯量形式 1 11 0 2 12 0 1 0 1 2 21 0 2 22 0 2 0 2 1 0 2 2 0 0 ( ) ( ) . ( ) ( ) ( ) . ( ) . ( ) ( ) . ( ) n n n n n n n n nn n c x t c x t c x t c x t c x t c x t c x t c x t c x t + + + = + + + = + + + = 把(5.20)看作是以 为未知量的非齐次线性方程组.这方 程组的系数行列式为 . 1 2 , ,., n c c c 0 W t( ) 由于 线性无关, 1 ( ),., ( ) x t x t n 0 = W t( ) 0 (5.20) ,故 有唯一解 1 2 , ,., c c cn 由定理2.知, 1 1( ) . ( ) n n c x t c x t + + 为(5.15)的解,且 线性微分方程组的一般理论