
§2.3恰当方程与积分因子 讲授内容: :恰当方程极其解法;积分因子概念利用积分因子求解一解 微分方程。 教学重点: 恰当方程的判定及求解方法,积分因子的概念, 1.恰当方程(全微分方程) 例2.15 例2.16 2.积分因子 例2.17 例2.18 例2.19 例2.20 例2.21 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 §2.3 恰当方程与积分因子 1.恰当方程(全微分方程) 例2.15 2.积分因子 例2.16 例2.17 例2.18 例2.19 例2.20 例2.21 :恰当方程极其解法;积分因子概念利用积分因子求解一解 微分方程. 恰当方程的判定及求解方法,积分因子的概念. 讲授内容: 教学重点:

§2.3恰当方程与积分因子 1.恰当方程(全微分方程) 考虑微分形式的一阶方程 M(x,y)dx+N(x,y)dy =0 (2.28) 其中M,N具有一阶连续的偏导数,这样的形式有时更便于寻找它 的通解.如果上式左端恰好是某个二元函数 u(x的全微分即 du(x,y)=M(x,y)d+N(x,y)dy (2.29) 则称(2.28)为全微分(恰当)方程. 例如 xdx+ydy =0 就是一个恰当方程.因为它的左端x+y恰好是二元函数 4(x,)=(的全徽分又如 yoc -xay =0 +J>2 结束 上一页返回下页<2 首页
结束 帮助 上一页 返回 下一页 目录 首页 1.恰当方程(全微分方程) 考虑微分形式的一阶方程 M x y dx N x y dy ( , ) ( , ) 0 (2.28) + = 其中M,N具有一阶连续的偏导数,这样的形式有时更便于寻找它 的通解.如果上式左端恰好是某个二元函数 u x y ( , ) 的全微分即 du x y M x y dx N x y dy ( , ) ( , ) ( , ) (2.29) = + 则称(2.28)为全微分(恰当)方程. xdx ydy + = 0 例如 §2.3 恰当方程与积分因子 就是一个恰当方程 .因为它的左端 xdx+ydy 恰好是二元函数 的全微分.又如 1 2 2 ( , ) ( ) 2 u x y x y = + 2 2 0 ydx xdy x y − = +

§2.3恰当方程与积分因子 M(x,y)dx+N(x,y)dy =0 (2.28) du(x,y)=M(x,y)dx+N(x,y)dy (2.29) 也是一个恰当方程因为它的左端为 4(x,)=的堆微分. 如果(2.28)是恰当方程,则由定义存在可微的二元函数(x使嫩 得(2.29)成立.从而由(2.28)知 du(x,y)≡0 于是 u(x,y)=c 为(2.28)的解这里c为任意常数 那么如何求解2.28)呢?下面就以下三个问题进行讨论: 1.如何判断(2.28)是否为全微分方程; 2.若(2.28)为全微分方程,如何求出二元函数(x,y); 3.若(2.28)不是全微分方程,有何办法将它转变成全微分方程并 求出其通解。 结束 帮助 返叵
结束 帮助 上一页 返回 下一页 目录 首页 §2.3 恰当方程与积分因子 也是一个恰当方程.因为它的左端为 ( , ) 的全微分. x u x y arctg y = 如果(2.28)是恰当方程,则由定义存在可微的二元函数 使 得(2.29)成立.从而由(2.28)知 u x y ( , ) du x y ( , ) 0 于是 u x y c ( , ) = M x y dx N x y dy ( , ) ( , ) 0 (2.28) + = du x y M x y dx N x y dy ( , ) ( , ) ( , ) (2.29) = + 为(2.28)的解.这里c 为任意常数. 那么如何求解(2.28)呢?下面就以下三个问题进行讨论: 1. 如何判断(2.28)是否为全微分方程; 2. 若(2.28)为全微分方程,如何求出二元函数 u x y ( , ) ; 3. 若(2.28)不是全微分方程,有何办法将它转变成全微分方程并 求出其通解
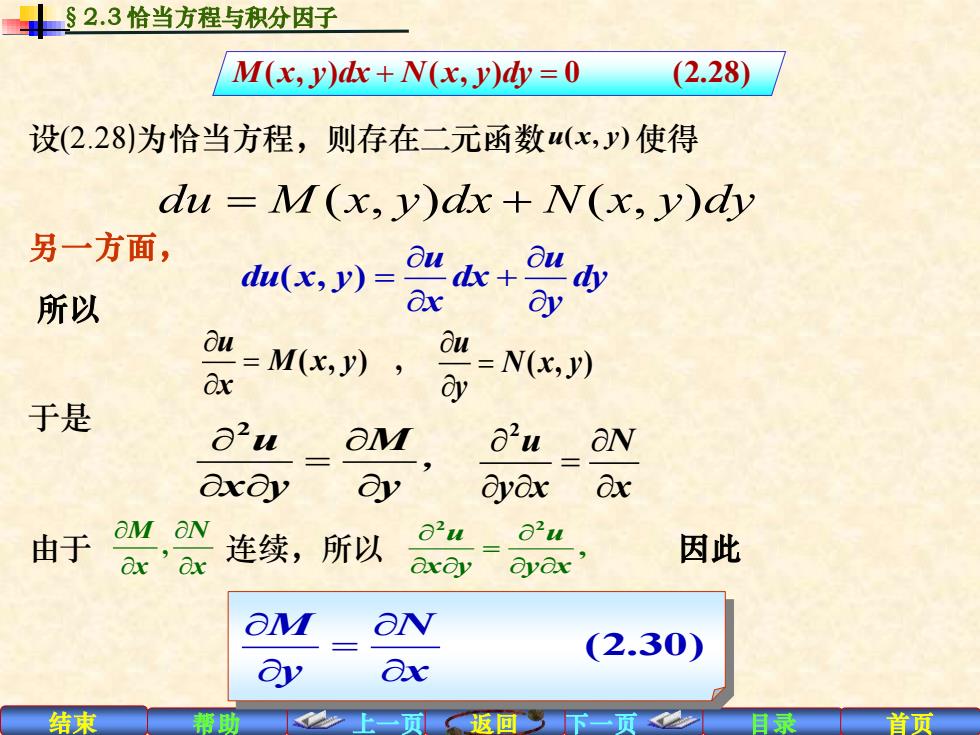
$2.3恰当方程与积分因子 M(x,y)dx+N(x,y)dy=0 (2.28) 设(2.28)为恰当方程,则存在二元函数(x,y)使得 du=M(x,y)dx+N(x,y)dy 另一方面, du(x,y)= 所以 Ox ay ou Ox =M(x,y) Ou=N(x,y) oy 于是 Ou aM a'u aN axay ay oyax Ox 由于 OM X 连续,) 所以 8u 8u ax’ axay 因此 ayax aM aN (2.30) ay Ox 结束 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 设(2.28)为恰当方程,则存在二元函数 u x y ( , ) 使得 §2.3 恰当方程与积分因子 另一方面, ( , ) u u du x y dx dy x y = + M x y dx N x y dy ( , ) ( , ) 0 (2.28) + = du M x y dx N x y dy = + ( , ) ( , ) ( , ) , u M x y x = ( , ) u N x y y = 所以 于是 2 u M x y y = , 2 u N y x x = 由于 , 连续,所以 M N x x = 2 2 , u u x y y x 因此 (2.30) M N y x =

§2.3恰当方程与积分因子 aM aN M(x,y)dx+N(x,y)dy=0 (2.28) (2.30) ay ax (2.30)是(2.28)为恰当方程的必要条件 下面证明,如果(2.30)成立,则(2.28)为恰当方程, 我们取函数(x,y)如下 u(x,y)=M(x,y)dx+o(y) (2.31) 其中当进行积分是,把y看成参数,而p(为任一个y的可微函数 实际上由0=M将看成参数解此方程,得) u(c,y)=「M(x,y)dc+c 当c取为y的可微函数(时,仍然是 的解 为了使函数(的尘微分等于(2.28)的左端,还应当要求函数 满足u(x,y) 即要求p(满足 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 (2.30)是(2.28)为恰当方程的必要条件. 下面证明,如果(2.30)成立,则(2.28)为恰当方程. 我们取函数 u x y ( , ) 如下 u x y M x y dx y ( , ) ( , ) ( ) (2.31) = + 其中当进行积分是,把 y 看成参数,而 ( y 为任一个 ) y 的可微函数 u x y M x y dx c ( , ) ( , ) = + ( , ) u M x y x = (实际上由 ,将 y 看成参数解此方程,得) ( y) ( , ) u M x y x = 当 c取为y的可微函数 时,仍然是 的解) §2.3 恰当方程与积分因子 = (2.30) M N y x M x y dx N x y dy ( , ) ( , ) 0 (2.28) + = 为了使函数 的全微分等于(2.28)的左端,还应当要求函数 满足 u x y ( , ) u x y ( , ) ( ) ( , ) ( , ) u d y M x y dx N x y y y dy = + = 即要求( ) 满足y

$2.3恰当方程与积分因子 do(y) =N(x,y)- M(x,y)d (2.32) 少 vvrvwrwwvwrrrrrrvwwwrrrvrvrvrvrvwvrrrrrrvrr 显然只要上式右端与x无关,把它的两边对y积分一次即得p(代入 (2.31)就找到其全微分为(2.28)左端的u(x,下面说明(2.32)右端与x 无关 事实上,由于M(x续可微,因此根据条件(2.30) aM aN (2.30) lNWwa1=x-Ma ax aN ∫Mx,)= aN aM =0 注: 这里用到了含参变量积分的性质:若f(x,y),f进续,则 寻∫g 茵此在涤件(2.30j得到满足的条件下,为了求出c,位.31)满边对y积 分得 p))=jiN(x,y)-a∫Mx,y1 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 ( ) ( , ) ( , ) (2.32) d y N x y M x y dx dy y = − 显然只要上式右端与x无关,把它的两边对y积分一次即得 代入 (2.31)就找到其全微分为(2.28)左端的 .下面说明(2.32)右端与x 无关. ( y) u x y ( , ) 事实上,由于 连续可微,因此根据条件(2.30) M x y ( , ) §2.3 恰当方程与积分因子 [ ( , ) ( , ) ] [ ( , ) ] N N x y M x y dx M x y dx x y x x y − = − [ ( , ) ] 0 N N M M x y dx x y x x y = − = − = (2.30) M N y x (这里用到了含参变量积分的性质:若 f x y f x y ( , ), ' ( , ) 连续 y ,则 ( , ) f f x y dx dx y y = ) 注: 因此在条件(2.30)得到满足的条件下,为了求出 ,(2.31)两边对y积 分得 u x y ( , ) ( ) [ ( , ) ( , ) ] y N x y M x y dx dy y = −

§2.3恰当方程与积分因子 du(x,y)=M(x,y)d+N(x,y)dy (2.29) 将此式代入(2.29)从而求出 ,MC+jN(x,-∫Mx,I 这样我们得出(2.28)为全微分方程的充分必要条件是(2.30)成立 如果对于(2.28),(2.30)成立,那么它的通解为: ∫Mx,Jy)+∫Nx,y)-∫JM(x,yxw=e 用类此的方法可推导出其通解为: ∫Mx,y)+∫Nx,y)-∫N(x,yw=c 其通解也可以用下面的定积分来求: 或 ∫M(x,)+∫N(,y)=c 其中(xo,是M化,y),N,y)及其偏导数连续的区域内的任意一点 结束 帮助 返▣
结束 帮助 上一页 返回 下一页 目录 首页 这样我们得出(2.28)为全微分方程的充分必要条件是(2.30)成立. §2.3 恰当方程与积分因子 将此式代入(2.29)从而求出 u x y M x y dx N x y dy M x y dx dy ( , ) ( , ) ( , ) [ ( , ) ] = + − 如果对于(2.28),(2.30)成立,那么它的通解为: M x y dx N x y dx M x y dx dy c ( , ) ( , ) [ ( , ) ] y + − = 用类此的方法可推导出其通解为: M x y dx N x y dx N x y dy dx c ( , ) ( , ) [ ( , ) ] y + − = 其通解也可以用下面的定积分来求: 或 0 0 0 ( , ) ( , ) x y x y M x y dx N x y dy c + = 其中 (x0 , y是 0 )M(x,y),N(x,y)及其偏导数连续的区域内的任意一点. du x y M x y dx N x y dy ( , ) ( , ) ( , ) (2.29) = +
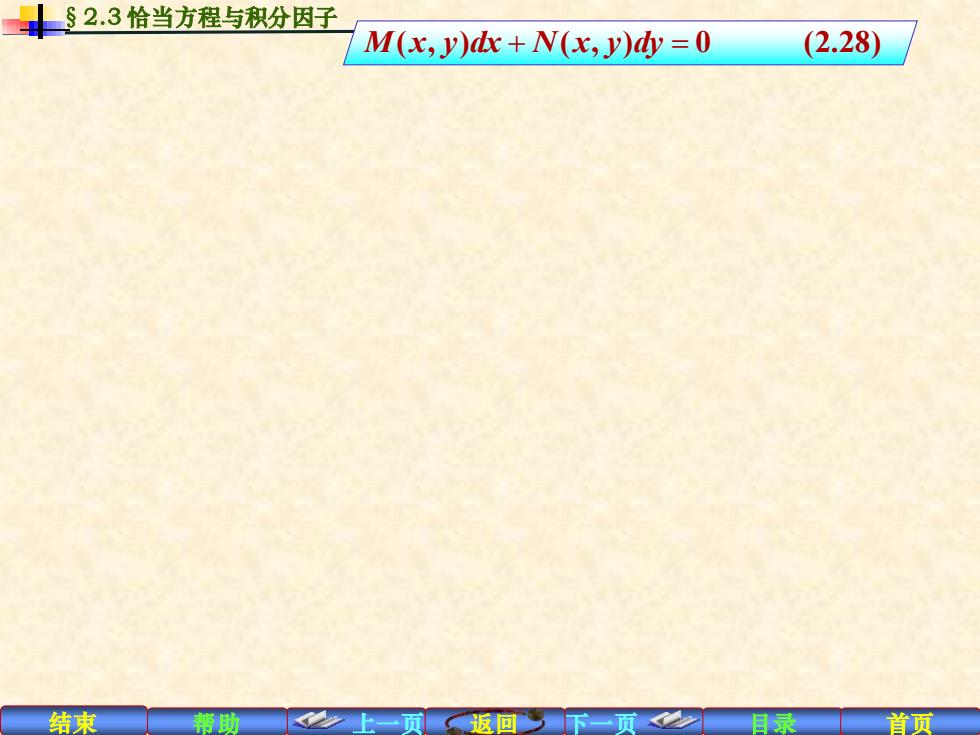
§2.3恰当方程与积分因子 M(x,y)dx+N(x,y)dy=0 (2.28) 结束 精助2上一贡返回下页2目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 §2.3 恰当方程与积分因子 M x y dx N x y dy ( , ) ( , ) 0 (2.28) + =

§2.3恰当方程与积分因子 例2.15求解微分方程 w+2(2+y=0 解:方法一 由于 号-x联,此方程为恰当方程 OM x,)-∫sc+2e2+y-∫gw ixy-xy 故通解为 2x2y+y2=c 或 (d-e 得 22y+ 42=G 结束 帮助 返正
结束 帮助 上一页 返回 下一页 目录 首页 例2.15 求解微分方程 1 2 ( ) 0 2 xydx x y dy + + = 解: 方法一. 由于 , 因此,此方程为恰当方程 M N x y x = = 1 2 ( , ) ( ) [ ] 2 u x y xydx x y dy xydx dy y = + + − 1 1 1 1 1 1 2 2 2 2 2 2 ( ) 2 2 2 2 2 4 = + + − = + x y x y y x y x y y 故通解为 2 2 2x y y c + = §2.3 恰当方程与积分因子 或 0 0 1 (0 ) 2 x y xydx y dy c + + = 得 1 1 2 2 2 4 x y y C + =

一L§2.3恰当方程与积分因子 如果判断一个方程为恰当方程,并不需按照上述方法求解,而是采 用“分项组合法”· 方法二 利用分项组合的办法即凑微分法. +22+z=0d3x2y)+d)=0 y+)=0通解为x+子- 1 即 2x2y+y=c :=4) 例2.16求解微分方程 解: -方程为恰当方程 aM=-1 故通解为 (cosx+(10)do-C,sinx+C 2 y 结束 目录 首页
结束 帮助 上一页 返回 下一页 目录 首页 §2.3 恰当方程与积分因子 利用分项组合的办法 即 凑微分法. 方法二. 1 1 2 0 2 2 xydx x dy ydy + + = 如果判断一个方程为恰当方程,并不需按照上述方法求解,而是采 用“分项组合法”. 1 1 2 2 ( ) ( ) 0 2 4 d x y d y + = 1 1 2 2 ( ) 0 2 4 d x y y + = ∴通解为 1 1 2 2 2 4 x y y c + = 即 2 2 2 ( 4 ) x y y c c c + = = 例2.16 求解微分方程 2 1 1 (cos ) ( ) 0. + + − = x x dx dy y y y 解: ∵ ∴ 2 此方程为恰当方程 M N 1 y y x = − = 故通解为 x y x dx dy C y y + + − = 0 1 1 1 (cos ) ( 0) , 即 sin ln + + = x x y C y